【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,電磁誘導に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。ただし,\( \ \boldsymbol {E} \ \),\( \ \boldsymbol {B} \ \)はそれぞれ電界ベクトル及び磁束密度ベクトルを表す。
一般に,空間に固定されたループ(閉曲線)\( \ C \ \)に発生する起電力\( \ V \ \)は,
\[
\begin{eqnarray}
V&=&\oint_C \boldsymbol {E}\cdot \mathrm {d}\boldsymbol {l} ······························· ① \\[ 5pt ]
\end{eqnarray}
\]
と表される。ここで,\( \ \mathrm {d}\boldsymbol {l} \ \)はループに沿った線素ベクトルである。\( \ \fbox { (1) } \ \)の定理を適用すると,①式は,
\[
\begin{eqnarray}
V&=&\int_S \left( \nabla \times \boldsymbol {E}\right)\cdot \boldsymbol {n}\mathrm {d}S ······················· ①^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
と変形できる。ただし,\( \ S \ \)はループ\( \ C \ \)に囲まれた面,\( \ \boldsymbol {n} \ \)はその面の単位法線ベクトル,\( \ \mathrm {d}S \ \)は面素である。磁束密度\( \ \boldsymbol {B} \ \)が時間 \( \ t \ \)に応じて変化する場合には,マクスウェル方程式
\[
\begin{eqnarray}
\nabla \times \boldsymbol {E}&=& \ \fbox { (2) } \ ·························· ② \\[ 5pt ]
\end{eqnarray}
\]
を\( \ ①^{\prime } \ \)式に代入し,面\( \ S \ \)を貫く磁束は\( \ \displaystyle \mathit {\Phi }= \int_S \boldsymbol {B}\cdot \boldsymbol {n}\mathrm {d}S \ \)と表せることを用いると,
\[
\begin{eqnarray}
V&=& \ \fbox { (3) } \ ······························ ①^{\prime \prime } \\[ 5pt ]
\end{eqnarray}
\]
のようにファラデーの法則が得られる。
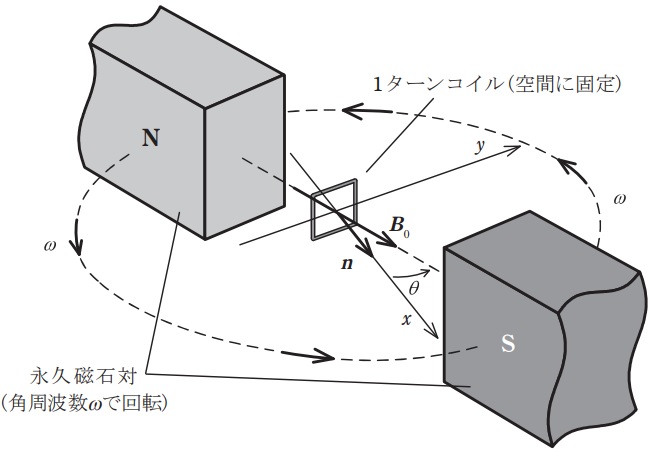
図のように,座標原点を中心として対向する永久磁石が形成する一様な磁束密度\( \ B_{0} \ \)の中に,一辺の長さが\( \ a \ \)の正方形状の\( \ 1 \ \)ターンコイルが設置されており,コイル面の法線ベクトルは \( \ x \ \)軸の方向を向いている。永久磁石対は座標原点を中心として\( \ xy \ \)平面内を角速度\( \ \omega \ \)で回転しており,磁界と\( \ x \ \)軸とのなす角は\( \ \theta =\omega t \ \)と表される。このとき,磁束密度のコイル面法線方向成分は\( \ \boldsymbol {B}\cdot \boldsymbol {n}= \ \fbox { (4) } \ \)となるので,上記の関係式を用いてコイルに発生する交流起電力を求めることができる。
例えば,\( \ 1 \ \mathrm {T} \ \)の磁束密度を発生する永久磁石対が毎分\( \ 3 \ 000 \ \)回転している場合を考えると,一辺の長さ\( \ a=10 \ \mathrm {cm} \ \)の正方形状の\( \ 1 \ \)ターンコイルに発生する交流起電力の振幅はおよそ\( \ \fbox { (5) } \ \mathrm {V} \ \)となる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& B_{0}\sin \omega t &(ロ)& \boldsymbol {E}\times \boldsymbol {B} &(ハ)& B_{0}\cos \omega t \\[ 5pt ]
&(ニ)& B_{0}\tan \omega t &(ホ)& 300 &(ヘ)& ガウス \\[ 5pt ]
&(ト)& 3 &(チ)& -\int \mathit {\Phi} \mathrm {d}t &(リ)& -\frac {\mathrm {d}\mathit {\Phi}}{\mathrm {d}t} \\[ 5pt ]
&(ヌ)& \nabla \cdot \boldsymbol {B} &(ル)& ストークス &(ヲ)& ヘルムホルツ \\[ 5pt ]
&(ワ)& \nabla \times \boldsymbol {B} &(カ)& 0.03 &(ヨ)& -\frac{ \partial \boldsymbol {B} }{ \partial t } \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
マクスウェル方程式からファラデーの電磁誘導を導き出し,コイルに発生する交流起電力を求める問題です。内容は電磁気ですが,中身はほぼ数学の式変形の問題です。
電験としては少し特殊な問題となりますが,\( \ 1 \ \)種では高い数学力が問われるので,本問の式の意味が全くわからない方は大学の数学の参考書等を確認してみるようにして下さい。
1.内積
二つのベクトル\( \ \boldsymbol A \ \)及び\( \ \boldsymbol B \ \)がある際に,そのなす角が\( \ \theta \ \)であるとき,内積\( \ \boldsymbol A \cdot \boldsymbol B \ \)は,
\[
\begin{eqnarray}
\boldsymbol A \cdot \boldsymbol B &=&\left| \boldsymbol A\right| \left| \boldsymbol B\right| \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
で定義されます。交流回路において,電圧と電流から有効電力を求める式は内積と同じになります。
2.\( \ \mathrm {rot} \ \)(回転)
数学における\( \ \mathrm {rot} \ \)(回転)は,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol E&=&\left( \frac { \partial E_{\mathrm {z}}}{ \partial y }-\frac { \partial E_{\mathrm {y}}}{ \partial z },\frac { \partial E_{\mathrm {x}}}{ \partial z }-\frac { \partial E_{\mathrm {z}}}{ \partial x },\frac { \partial E_{\mathrm {y}}}{ \partial x }-\frac { \partial E_{\mathrm {x}}}{ \partial y }\right) \\[ 5pt ]
\end{eqnarray}
\]
で定義され,外積を用いて表すと,
\[
\begin{eqnarray}
\mathrm {rot} \boldsymbol E &=& \nabla \times \boldsymbol E \\[ 5pt ]
&=& \begin{vmatrix} \mathrm {i} & \mathrm {j} & \mathrm {k} \\ \displaystyle \frac { \partial }{ \partial x } & \displaystyle \frac { \partial }{ \partial y } & \displaystyle \frac { \partial }{ \partial z } \\ E_{\mathrm {x}} & E_{\mathrm {y}} & E_{\mathrm {z}} \end{vmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となります。
(\( \ \mathrm {i} \ \),\( \ \mathrm {j} \ \),\( \ \mathrm {k} \ \)は\( \ x \ \)軸,\( \ y \ \)軸,\( \ z \ \)軸の単位ベクトルです)
3.ストークスの定理
面積分と線積分を対応させる定理で,マクスウェルの方程式からアンペールの周回積分の法則を導き出す際等に用いられる定理です。
\[
\begin{eqnarray}
\int _{\mathrm {S}}\left( \nabla \times \boldsymbol E\right) \mathrm {d}\boldsymbol S &=&\int _{\mathrm {C}}\boldsymbol E \cdot \mathrm {d}\boldsymbol l \\[ 5pt ]
\end{eqnarray}
\]
4.マクスウェル方程式(微分形)
電磁気における各性質を4つの式にまとめたものです。
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol D &=&\rho &⇔& \nabla \cdot \boldsymbol D &=&\rho \\[ 5pt ]
\mathrm {div} \boldsymbol B &=&0 &⇔& \nabla \cdot \boldsymbol B &=&0 \\[ 5pt ]
\mathrm {rot} \boldsymbol H &=&i+\displaystyle \frac { \partial \boldsymbol D}{ \partial t } &⇔& \nabla \times \boldsymbol H &=&i+\displaystyle \frac { \partial \boldsymbol D}{ \partial t } \\[ 5pt ]
\mathrm {rot} \boldsymbol E &=&-\displaystyle \frac { \partial \boldsymbol B}{ \partial t } &⇔& \nabla \times \boldsymbol E &=&-\displaystyle \frac { \partial \boldsymbol B}{ \partial t } \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ル
題意より解答候補は,(ヘ)ガウス,(ル)ストークス,(ヲ)ヘルムホルツ,になると思います。
ワンポイント解説「3.ストークスの定理」の通り,問題文における式変形はストークスの定理を用いた変形となります。
(2)解答:ヨ
ワンポイント解説「4.マクスウェル方程式」の通り,
\[
\begin{eqnarray}
\nabla \times \boldsymbol E &=&-\displaystyle \frac { \partial \boldsymbol B}{ \partial t } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
\( \ ② \ \)式を\( \ ①^{\prime } \ \)式に代入すると,
\[
\begin{eqnarray}
V&=&\int_S \left( -\frac { \partial \boldsymbol B}{ \partial t }\right)\cdot \boldsymbol {n}\mathrm {d}S \\[ 5pt ]
&=&\int_S \left( -\frac { \partial }{ \partial t }\boldsymbol B\cdot \boldsymbol {n}\right) \mathrm {d}S \\[ 5pt ]
&=&-\frac { \partial }{ \partial t }\int_S \boldsymbol B\cdot \boldsymbol {n}\mathrm {d}S \\[ 5pt ]
\end{eqnarray}
\]
となり,問題文より,\( \ \displaystyle \mathit {\Phi }= \int_S \boldsymbol {B}\cdot \boldsymbol {n}\mathrm {d}S \ \)であるから,\( \ \mathit {\Phi } \ \)が時間変化のみの関数であるとすれば,
\[
\begin{eqnarray}
V&=&-\frac {\mathrm {d}\mathit {\Phi}}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
磁束密度のコイル面法線方向成分は,\( \ \boldsymbol {n} \ \)はその面の単位法線ベクトルであり,その大きさは\( \ 1 \ \)であるから,ワンポイント解説「1.内積」の通り,
\[
\begin{eqnarray}
\boldsymbol {B}\cdot \boldsymbol {n}&=&B_{0}\times 1 \times \cos \theta \\[ 5pt ]
&=&B_{0}\cos \omega t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ト
(3),(4)より,
\[
\begin{eqnarray}
V&=&-\frac { \partial }{ \partial t }\int_S \boldsymbol B\cdot \boldsymbol {n}\mathrm {d}S \\[ 5pt ]
&=&-\frac { \partial }{ \partial t }\int_S B_{0}\cos \omega t \mathrm {d}S \\[ 5pt ]
&=&-\frac { \partial }{ \partial t }\left( B_{0}a^{2}\cos \omega t\right) \\[ 5pt ]
&=& B_{0}a^{2}\omega \sin \omega t \\[ 5pt ]
\end{eqnarray}
\]
となるので,その振幅の大きさ\( \ B_{0}a^{2}\omega \ \)は,\( \ B_{0}=1 \ \mathrm {[T]} \ \),\( \ a=0.1 \ \mathrm {[m]} \ \),\( \ \displaystyle \omega =\frac {2\pi \times 3 \ 000}{60}=100\pi \ \mathrm {[rad / s]} \ \)を代入すると,
\[
\begin{eqnarray}
B_{0}a^{2}\omega &=&1\times 0.1^{2} \times 100\pi \\[ 5pt ]
&≒& 3.14 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん