【問題】
【難易度】★★★☆☆(普通)
次の文章は,演算増幅器を用いた回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
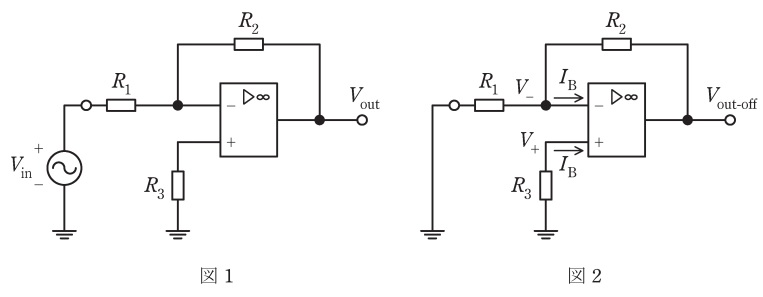
図1の回路において演算増幅器が理想的であるとき,演算増幅器の入力端子には電流が流れず,出力電圧\( \ V_{\mathrm {out}} \ \)は\( \ \ \fbox { (1) } \ \)\( \ V_{\mathrm {in}} \ \)となる。
次に,演算増幅器の入力端子に直流電流\( \ I_{\mathrm {B}} \ \)が流れている場合を考える。ただし,演算増幅器のその他の特性は理想的であるとする。このとき,図2のように回路の入力端子を接地し\( \ V_{\mathrm {in}}=0 \ \)としても出力電圧は零とならず\( \ V_{\mathrm {out-off}} \ \)となる。この\( \ V_{\mathrm {out-off}} \ \)を求める。図2の非反転入力端子の電位\( \ V_{\mathrm {+}} \ \)は,直流電流\( \ I_{\mathrm {B}} \ \)により,
\[
\begin{eqnarray}
V_{\mathrm {+}}&=& \ \fbox { (2) } ・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,反転入力端子の電位\( \ V_{\mathrm {-}} \ \)は,\( \ R_{\mathrm {1}} \ \)と\( \ R_{\mathrm {2}} \ \)からなる回路において\( \ I_{\mathrm {B}} \ \)と\( \ V_{\mathrm {out-off}} \ \)の重ねの理を考えることで,
\[
\begin{eqnarray}
V_{\mathrm {-}}&=& \ \fbox { (3) }I_{\mathrm {B}}+\frac {R_{\mathrm {1}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}V_{\mathrm {out-off}} ・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
と得られる。\( \ V_{\mathrm {+}}=V_{\mathrm {-}} \ \)であることを用いて①及び②式から\( \ V_{\mathrm {+}} \ \)と\( \ V_{\mathrm {-}} \ \)を消去すると,
\[
\begin{eqnarray}
V_{\mathrm {out-off}}&=& \ \fbox { (4) } ・・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
が得られる。③式は演算増幅器の入力端子に直流電流\( \ I_{\mathrm {B}} \ \)が流れると入力電圧が零であっても出力電圧に直流電圧(オフセット電圧)が現れることを示している。③式より,\( \ V_{\mathrm {out-off}} \ \)を\( \ I_{\mathrm {B}} \ \)によらず常に零とするためには,
\[
\begin{eqnarray}
R_{\mathrm {3}}&=& \ \fbox { (5) } \\[ 5pt ]
\end{eqnarray}
\]
とすれば良いことが分かる。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& -R_{\mathrm {2}}I_{\mathrm {B}} &(ロ)& -R_{\mathrm {1}} &(ハ)& \frac {R_{\mathrm {1}}+R_{\mathrm {2}}}{R_{\mathrm {1}}}\left( R_{\mathrm {1}}+R_{\mathrm {2}}-R_{\mathrm {3}}\right) I_{\mathrm {B}} \\[ 5pt ]
&(ニ)& R_{\mathrm {1}}+R_{\mathrm {2}} &(ホ)& R_{\mathrm {1}} &(ヘ)& -\frac {R_{\mathrm {2}}}{R_{\mathrm {1}}} \\[ 5pt ]
&(ト)& -\frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}} &(チ)& -\frac {R_{\mathrm {1}}}{R_{\mathrm {2}}} &(リ)& \frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}} \\[ 5pt ]
&(ヌ)& \frac {R_{\mathrm {1}}+R_{\mathrm {2}}}{R_{\mathrm {1}}}\left( \frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}-R_{\mathrm {3}}\right) I_{\mathrm {B}} &(ル)& -\left( R_{\mathrm {1}}+R_{\mathrm {2}}\right) &(ヲ)& \frac {R_{\mathrm {1}}+R_{\mathrm {2}}}{R_{\mathrm {1}}} \\[ 5pt ]
&(ワ)& -R_{\mathrm {3}}I_{\mathrm {B}} &(カ)& -R_{\mathrm {1}}I_{\mathrm {B}} &(ヨ)& \frac {R_{\mathrm {1}}+R_{\mathrm {2}}}{R_{\mathrm {1}}}\left( R_{\mathrm {1}}-R_{\mathrm {3}}\right) I_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
演算増幅器に関する問題ですが,\( \ 1 \ \)種の場合はなかなかストレートな問題が出題されません。
ただし,あらゆる公式や法則の基本を理解していれば,文章を読みながら答えられる問題も多く,本問もその典型的な問題と言えると思います。
問6か問7を選択するか迷うところですが,令和2年の合格率の高さを考えるとどちらの問題を選んでもそれなりの正答率があったと予想されます。
1.重ね合わせ(重ね)の理
複数の電源で構成された回路は,電源毎に計算した電流を重ね合わせて求めることができます。この時,電圧源は短絡,電流源は開放します。
本問においては演算増幅器の入力端子に流れる電流\( \ I_{\mathrm {B}} \ \)を電流源として考えると良いでしょう。
2.理想的な演算増幅器の特徴
1.電圧増幅率が無限大である。したがって,無限大でない有限数が出力される時,入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)(バーチャルショート)となる。
2.入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
3.出力インピーダンスがゼロである。

【関連する「電気の神髄」記事】
【解答】
(1)解答:ヘ
図1の回路において,入力端子間に電流は流れず\( \ R_{\mathrm {3}} \ \)を流れる電流は零であるため,演算増幅器の+端子の電圧\( \ V_{\mathrm {+}} \ \)及び−端子の電圧\( \ V_{\mathrm {-}} \ \)ともに零である。したがって,\( \ R_{\mathrm {1}} \ \)を流れる電流\( \ I_{\mathrm {1}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {1}}&=&\frac {V_{\mathrm {in}}}{R_{\mathrm {1}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ I_{\mathrm {1}} \ \)はそのまま\( \ R_{\mathrm {2}} \ \)を流れるため,出力端子\( \ V_{\mathrm {out}} \ \)の電位は,
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&V_{\mathrm {+}}-R_{\mathrm {2}}I_{\mathrm {1}} \\[ 5pt ]
&=&0-R_{\mathrm {2}}\cdot \frac {V_{\mathrm {in}}}{R_{\mathrm {1}}} \\[ 5pt ]
&=&-\frac {R_{\mathrm {2}}}{R_{\mathrm {1}}}V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ワ
図2の演算増幅器の+端子の電位\( \ V_{\mathrm {+}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {+}}&=&0-R_{\mathrm {3}}I_{\mathrm {B}} \\[ 5pt ]
&=&-R_{\mathrm {3}}I_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
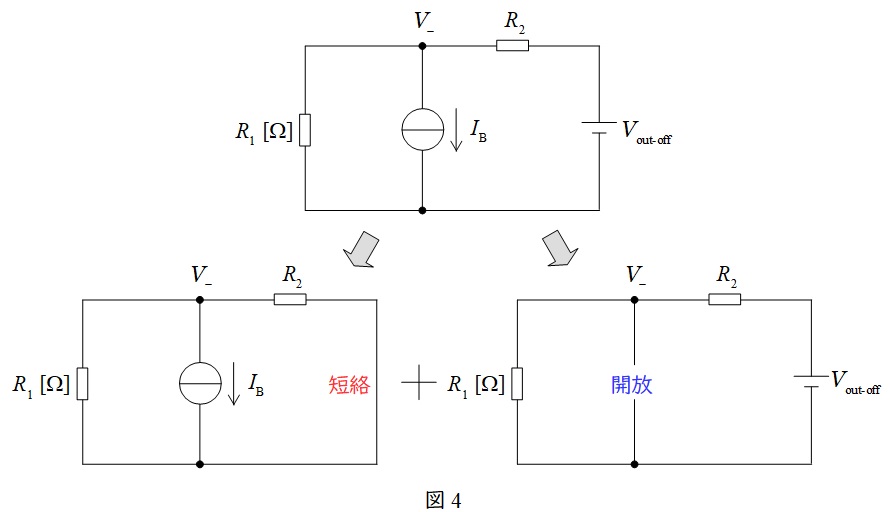
演算増幅器の入力端子に流れる電流\( \ I_{\mathrm {B}} \ \)を電流源として考えると,等価回路は図4上段のように描くことができ,さらにワンポイント解説「1.重ね合わせ(重ね)の理」により電圧源と電流源に分けると図4下段のように分けられる。
図4下段左図より,
\[
\begin{eqnarray}
I_{\mathrm {B}}&=&-\frac {V_{\mathrm {-}}}{R_{\mathrm {1}}}-\frac {V_{\mathrm {-}}}{R_{\mathrm {2}}} \\[ 5pt ]
&=&-\left( \frac {1}{R_{\mathrm {1}}}+\frac {1}{R_{\mathrm {2}}}\right) V_{\mathrm {-}} \\[ 5pt ]
&=&-\frac {R_{\mathrm {1}}+R_{\mathrm {2}}}{R_{\mathrm {1}}R_{\mathrm {2}}} V_{\mathrm {-}} \\[ 5pt ]
V_{\mathrm {-}}&=&-\frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}} I_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
となり,図4下段右図より,
\[
\begin{eqnarray}
V_{\mathrm {-}}&=&\frac {R_{\mathrm {1}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}V_{\mathrm {out-off}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,重ねの理により,
\[
\begin{eqnarray}
V_{\mathrm {-}}&=&-\frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}I_{\mathrm {B}}+\frac {R_{\mathrm {1}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}V_{\mathrm {out-off}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヌ
①式及び②式より,
\[
\begin{eqnarray}
V_{\mathrm {+}}&=&V_{\mathrm {-}} \\[ 5pt ]
-R_{\mathrm {3}}I_{\mathrm {B}}&=&-\frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}I_{\mathrm {B}}+\frac {R_{\mathrm {1}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}V_{\mathrm {out-off}} \\[ 5pt ]
\frac {R_{\mathrm {1}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}V_{\mathrm {out-off}}&=&\frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}I_{\mathrm {B}}-R_{\mathrm {3}}I_{\mathrm {B}} \\[ 5pt ]
V_{\mathrm {out-off}}&=&\frac {R_{\mathrm {1}}+R_{\mathrm {2}}}{R_{\mathrm {1}}}\left( \frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}I_{\mathrm {B}}-R_{\mathrm {3}}I_{\mathrm {B}}\right) \\[ 5pt ]
&=&\frac {R_{\mathrm {1}}+R_{\mathrm {2}}}{R_{\mathrm {1}}}\left( \frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}-R_{\mathrm {3}}\right) I_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:リ
\( \ V_{\mathrm {out-off}} \ \)を\( \ I_{\mathrm {B}} \ \)によらず常に零とするためには,③式のカッコ内\( \ \displaystyle \frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}-R_{\mathrm {3}} \ \)が零とならなければならない。したがって,
\[
\begin{eqnarray}
\frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}-R_{\mathrm {3}}&=&0 \\[ 5pt ]
R_{\mathrm {3}}&=&\frac {R_{\mathrm {1}}R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん