《理論》〈電子回路〉[H26:問7]MOSFETと抵抗を用いた回路に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

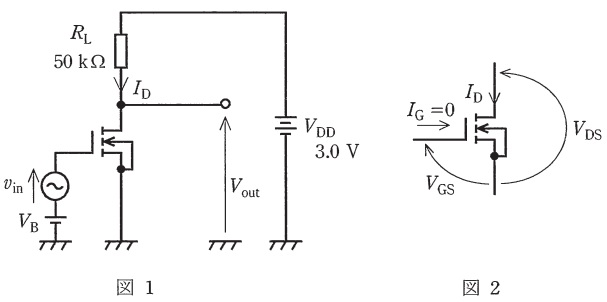
次の文章は，図1に示す$\ \mathrm {MOSFET} \ $と抵抗を用いた回路に関する記述である。文中の$\ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。ただし，$\ \mathrm {MOSFET} \ $のゲート-ソース間電圧$\ V_{\mathrm {GS}} \ $とドレーン‐ソース間電圧$\ V_{\mathrm {DS}} \ $は図2のとおりに定義され，両者が
$$\begin{eqnarray} 　V_{\mathrm {DS}} ≧ V_{\mathrm {GS}}-V_{\mathrm {T}} ＞ 0 \ 　　　　　　　　　・・・・・・・・・・① \\[ 5pt ] \end{eqnarray}$$ を満足するとき，ドレーン電流$\ I_{\mathrm {D}} \ $は
$$\begin{eqnarray} 　I_{\mathrm {D}} &=& K\left( V_{\mathrm {GS}}-V_{\mathrm {T}}\right) ^{2}　　　　　　　　　・・・・・・・・・・② \\[ 5pt ] \end{eqnarray}$$ で表されるものとする。ここで，$\ K \ $や$\ V_{\mathrm {T}} \ $は$\ \mathrm {MOSFET} \ $の特性を表す定数であり，また，ゲート電流$\ I_{\mathrm {G}} \ $は常に零であるとする。

図1の回路において，$\ \mathrm {MOSFET} \ $の$\ K \ $と$\ V_{\mathrm {T}} \ $をそれぞれ，$\ K=40 \ \mu \ \mathrm {S / V} \ $，$\ V_{\mathrm {T}}=0.50 \ \mathrm {V} \ $とし，抵抗$\ R_{\mathrm {L}} \ $を$\ 50 \ \mathrm {k\Omega } \ $，電源電圧$\ V_{\mathrm {DD}} \ $を$\ 3.0 \ \mathrm {V} \ $とする。

まず，入力信号$\ v_{\mathrm {in}} \ $が$\ 0.0 \ \mathrm {V} \ $のときを考える。図1の$\ \mathrm {MOSFET} \ $が①式の関係を満足するためには，$\ V_{\mathrm {B}} \ $は$\ \fbox {　 （１） 　} \ \mathrm {V} ≧ V_{\mathrm {B}} ＞ \fbox {　 （２） 　} \ \mathrm {V} \ $でなければならない。

次に，$\ v_{\mathrm {in}} \ $の大きさが十分に小さいとき，$\ V_{\mathrm {out}} \ $は
$$\begin{eqnarray} 　V_{\mathrm {out}} &=& V_{\mathrm {DD}}-R_{\mathrm {L}}K\left( V_{\mathrm {B}}+v_{\mathrm {in}}-V_{\mathrm {T}}\right) ^{2}　・・・・・・・・・・③ \\[ 5pt ] \end{eqnarray}$$ となる。

ここで，$\ v_{\mathrm {in}} \ $が$\ 0.0 \ \mathrm {V} \ $のときの$\ V_{\mathrm {out}} \ $を$\ V_{0} \ $とし，$\ v_{\mathrm {in}} \ $を加えたときに$\ V_{\mathrm {out}} \ $が$\ V_{0} \ $から変化した分を$\ \Delta V_{\mathrm {out}}=V_{\mathrm {out}}-V_{0} \ $とする。③式から$\ \Delta V_{\mathrm {out}} \ $を求めると，③式において$\ v_{\mathrm {in}} \ $の大きさが十分に小さいので$\ v_{\mathrm {in}} \ $の2乗の項を無視すると，$\ \Delta V_{\mathrm {out}} \ $は$\ \fbox {　 （３） 　} \ $となる。

以上の結果を踏まえて，$\ V_{\mathrm {B}} \ $を$\ 1.0 \ \mathrm {V} \ $とすると，$\ V_{0} \ $は$\ \fbox {　 （４） 　} \ \mathrm {V} \ $となる。このとき，$\ \Delta V_{\mathrm {out}} \ $を出力信号とすれば，図1の回路の増幅率$\ \displaystyle \frac {\Delta V_{\mathrm {out}}}{v_{\mathrm {in}}} \ $が$\ \fbox {　 （５） 　} \ $であることが分かる。

〔問7の解答群〕
$$\begin{eqnarray} &（イ）&　0.25　　　　　&（ロ）&　1.5　　　　　&（ハ）&　2.0 \\[ 5pt ] &（ニ）&　-2.0　　　　　&（ホ）&　4.0　　　　　&（ヘ）&　0.0 \\[ 5pt ] &（ト）&　3.0　　　　　&（チ）&　-2R_{\mathrm {L}}KV_{\mathrm {B}}v_{\mathrm {in}}　　　　　&（リ）&　-4.0 \\[ 5pt ] &（ヌ）&　0.50　　　　　&（ル）&　2.5　　　　　&（ヲ）&　2R_{\mathrm {L}}K\left( V_{\mathrm {B}}-V_{\mathrm {T}}\right) v_{\mathrm {in}} \\[ 5pt ] &（ワ）&　-0.50　　　　　&（カ）&　-2R_{\mathrm {L}}K\left( V_{\mathrm {B}}-V_{\mathrm {T}}\right) v_{\mathrm {in}}　　　　　&（ヨ）&　1.0 \end{eqnarray}$$

【ワンポイント解説】

本問は(1)が最も難しく，後半の問題はそれほど複雑な計算を要しないため，(1)に惑わされないように解く必要があります。全体としては特別な公式も使用することはなく，一種としては比較的オーソドックスな問題と言えると思います。

【解答】

(1)解答：ロ
(2)解答：ヌ
図1，2より$\ V_{\mathrm {GS}}=V_{\mathrm {B}} \ $である。
また，$\ V_{\mathrm {DS}} \ $は，
$$\begin{eqnarray} V_{\mathrm {DS}} &=& V_{\mathrm {DD}}-R_{\mathrm {L}}I_{\mathrm {D}} \\[ 5pt ] \end{eqnarray}$$ の関係があるので，これに②を代入し，各値を代入すると，
$$\begin{eqnarray} V_{\mathrm {DS}} &=& V_{\mathrm {DD}}-R_{\mathrm {L}}\cdot K\left( V_{\mathrm {GS}}-V_{\mathrm {T}}\right) ^{2} \\[ 5pt ] &=& -KR_{\mathrm {L}} V_{\mathrm {GS}} ^{2}+2KR_{\mathrm {L}} V_{\mathrm {T}}V_{\mathrm {GS}}-KR_{\mathrm {L}} V_{\mathrm {T}} ^{2}+V_{\mathrm {DD}} \\[ 5pt ] &=& -40\times 10^{-6}\times 50\times 10^{3} \times V_{\mathrm {B}} ^{2}+2\times 40\times 10^{-6}\times 50\times 10^{3} \times 0.50 \times V_{\mathrm {B}}-40\times 10^{-6}\times 50\times 10^{3}\times 0.50 ^{2}+3.0 \\[ 5pt ] &=& -2 V_{\mathrm {B}} ^{2}+2V_{\mathrm {B}}+2.5 \\[ 5pt ] \end{eqnarray}$$ となる。よって，①は，
$$\begin{eqnarray} 　V_{\mathrm {DS}} &≧& V_{\mathrm {B}}-V_{\mathrm {T}} &＞& 0 \\[ 5pt ] 　V_{\mathrm {DS}}+V_{\mathrm {T}} &≧& V_{\mathrm {B}} &＞& V_{\mathrm {T}} \\[ 5pt ] 　-2 V_{\mathrm {B}} ^{2}+2V_{\mathrm {B}}+2.5+0.5 &≧& V_{\mathrm {B}} &＞& 0.5 \\[ 5pt ] 　-2 V_{\mathrm {B}} ^{2}+2V_{\mathrm {B}}+3 &≧& V_{\mathrm {B}} &＞& 0.5 \\[ 5pt ] \end{eqnarray}$$ と整理でき，$\ -2 V_{\mathrm {B}} ^{2}+2V_{\mathrm {B}}+3≧V_{\mathrm {B}} \ $を解くと，
$$\begin{eqnarray} 　-2 V_{\mathrm {B}} ^{2}+2V_{\mathrm {B}}+3&≧&V_{\mathrm {B}} \\[ 5pt ] 　-2 V_{\mathrm {B}} ^{2}+V_{\mathrm {B}}+3&≧&0 \\[ 5pt ] 　2 V_{\mathrm {B}} ^{2}-V_{\mathrm {B}}-3&≦&0 \\[ 5pt ] 　\left( V_{\mathrm {B}}+1\right) \left( 2 V_{\mathrm {B}}-3\right) &≦&0 \\[ 5pt ] 　-1 ≦ V_{\mathrm {B}}&≦&1.5 \\[ 5pt ] \end{eqnarray}$$ となるので，(1)は(ロ)，(2)は(ヌ)となる。

(3)解答：カ
③より，
$$\begin{eqnarray} \Delta V_{\mathrm {out}} &=& V_{\mathrm {out}}-V_{0} \\[ 5pt ] &=& V_{\mathrm {DD}}-R_{\mathrm {L}}K\left( V_{\mathrm {B}}+v_{\mathrm {in}}-V_{\mathrm {T}}\right) ^{2} -\left[ V_{\mathrm {DD}}-R_{\mathrm {L}}K\left( V_{\mathrm {B}}-V_{\mathrm {T}}\right) ^{2}\right] \\[ 5pt ] &=& V_{\mathrm {DD}}- R_{\mathrm {L}}K\left( V_{\mathrm {B}}^{2}+v_{\mathrm {in}}^{2}+V_{\mathrm {T}}^{2}+2V_{\mathrm {B}}v_{\mathrm {in}}-2v_{\mathrm {in}}V_{\mathrm {T}}-2V_{\mathrm {T}}V_{\mathrm {B}}\right) \\[ 5pt ] && -\left[ V_{\mathrm {DD}}-R_{\mathrm {L}}K\left( V_{\mathrm {B}}^{2}-2V_{\mathrm {B}}V_{\mathrm {T}}+ V_{\mathrm {T}}^{2}\right) \right] \\[ 5pt ] &≃& -R_{\mathrm {L}}K\left( 2V_{\mathrm {B}}v_{\mathrm {in}}-2v_{\mathrm {in}}V_{\mathrm {T}}\right) \\[ 5pt ] &=&-2R_{\mathrm {L}}K\left( V_{\mathrm {B}}-V_{\mathrm {T}}\right) v_{\mathrm {in}} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(4)解答：ル
③に各値を代入すると，
$$\begin{eqnarray} V_{0} &=& V_{\mathrm {DD}}-R_{\mathrm {L}}K\left( V_{\mathrm {B}}-V_{\mathrm {T}}\right) ^{2} \\[ 5pt ] &=& 3.0-50\times 10^{3}\times 40\times 10^{-6} \times \left( 1.0-0.5\right) ^{2} \\[ 5pt ] &=& 2.5 \\[ 5pt ] \end{eqnarray}$$ と求められる。

(5)解答：ニ
(３)より，
$$\begin{eqnarray} \frac {\Delta V_{\mathrm {out}}}{v_{\mathrm {in}}} &=& -2R_{\mathrm {L}}K\left( V_{\mathrm {B}}-V_{\mathrm {T}}\right) \\[ 5pt ] &=& -2\times 50\times 10^{3}\times 40\times 10^{-6}\times \left( 1.0-0.5\right) \\[ 5pt ] &=& -2 \\[ 5pt ] \end{eqnarray}$$ と求められる。