《理論》〈電磁気〉[R03:問2]２つのコイルを使用した環状鉄心のインダクタンスに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，コイルのインダクタンスに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

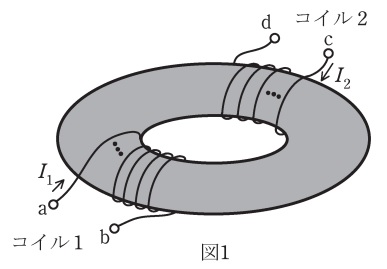
図1のように，環状鉄心にコイル$ \ 1 \ $とコイル$ \ 2 \ $が巻かれており，コイル$ \ 1 \ $の巻数とコイル$ \ 2 \ $の巻線の比は$ \ 1 : a \ $である。各コイルに電流が流れたときには鉄心の内部にのみ磁界が発生するものとする。

コイル$ \ 1 \ $の自己インダクタンスを$ \ L_{1} \ $とすると，コイル$ \ 2 \ $の自己インダクタンス$ \ L_{2} \ $は$ \ \fbox {　（１）　} \ $，コイル$ \ 1 \ $の端子$ \ \mathrm {ab} \ $とコイル$ \ 2 \ $の端子$ \ \mathrm {cd} \ $の間の相互インダクタンス$ \ M \ $は$ \ \fbox {　（２）　} \ $と表される。図1に示す向きに$ \ I_{1} \ $，$ \ I_{2} \ $の電流が各コイルに流れている場合には，蓄積された磁界のエネルギーは，
\[
\begin{eqnarray}
W&=&\frac {1}{2}L_{1}I_{1}^{2}+\frac {1}{2}L_{2}I_{2}^{2}+MI_{1}I_{2} \\[ 5pt ] \end{eqnarray}
\] と表されるので，$ \ I_{1}=-aI_{2} \ $の場合には磁界のエネルギーは$ \ \fbox {　（３）　} \ $となる。

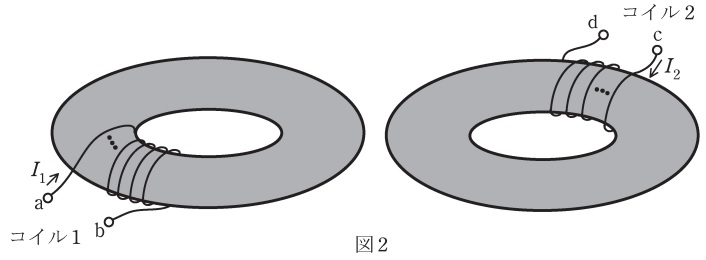
図1のコイル$ \ 1 \ $の端子$ \ \mathrm {b} \ $とコイル$ \ 2 \ $の端子$ \ \mathrm {c} \ $を接続すると，端子$ \ \mathrm {ad} \ $間の自己インダクタンスは$ \ \fbox {　（４）　} \ $となる。これに対して図2のように，図1で用いたものと同じ特性を有する$ \ 2 \ $個の環状鉄心にそれぞれ巻かれているコイル$ \ 1 \ $の端子$ \ \mathrm {b} \ $とコイル$ \ 2 \ $の端子$ \ \mathrm {c} \ $を接続した場合には，端子$ \ \mathrm {ad} \ $間の自己インダクタンスは$ \ \fbox {　（５）　} \ $となる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　aL_{1}　　　　　&（ロ）&　\frac {L_{1}}{\sqrt {a}}　　　　　&（ハ）&　\frac {L_{1}}{a^{2}} \\[ 5pt ] &（ニ）&　a^{2}L_{1}　　　　　&（ホ）&　\left( a+1\right) ^{2}L_{1}　　　　　&（ヘ）&　2L_{1}I_{1}^{2} \\[ 5pt ] &（ト）&　\left( a+1\right) L_{1}　　　　　&（チ）&　a^{3}L_{1}　　　　　&（リ）&　\left( a^{3}+1\right) L_{1} \\[ 5pt ] &（ヌ）&　\left( a^{2}+1\right) L_{1}　　　　　&（ル）&　\sqrt {a+1}L_{1}　　　　　&（ヲ）&　0 \\[ 5pt ] &（ワ）&　4a^{2}L_{1}I_{1}^{2}　　　　　&（カ）&　\frac {L_{1}}{a}　　　　　&（ヨ）&　\sqrt {\left| a-1\right| }L_{1} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

コイルの相互インダクタンスや合成インダクタンスに関する問題です。
公式としては$ \ 3 \ $種の頃から扱う公式ばかりなので，難解なものはありませんが，(1)がすんなり解けるかどうかが鍵となる問題です。
(1)の内容は非常に重要な内容となるので，しっかりと理解しておくようにしましょう。

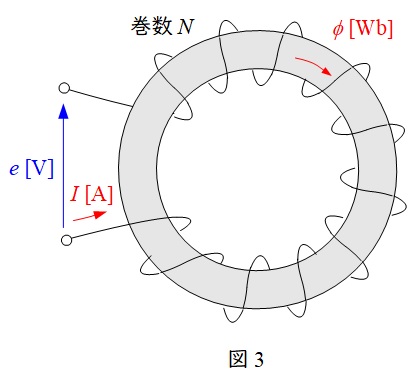
1.自己インダクタンス$ \ L \ $
図3のような環状ソレノイド回路において，巻数$ \ N \ $のコイルに電流$ \ I \ $を流した時の鉄心の磁束$ \ \phi \ $と比例定数$ \ L \ $の関係は，起電力$ \ e \ $を求める関係より，
\[
\begin{eqnarray}
-N\frac {\mathrm {d} \phi }{\mathrm {d} t}&=&-L\frac {\mathrm {d} I}{\mathrm {d} t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] L &=&\frac {N\phi }{I} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ L \ $を自己インダクタンスと言います。

2.相互インダクタンス$ \ M \ $
自己インダクタンス$ \ L_{1} \ $と$ \ L_{2} \ $のコイルがあった時の相互インダクタンス$ \ M \ $は，
\[
\begin{eqnarray}
M&=&k\sqrt {L_{1}L_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。この時，$ \ k \ $は結合係数と呼ばれ，$ \ 0≦k≦1 \ $となります。

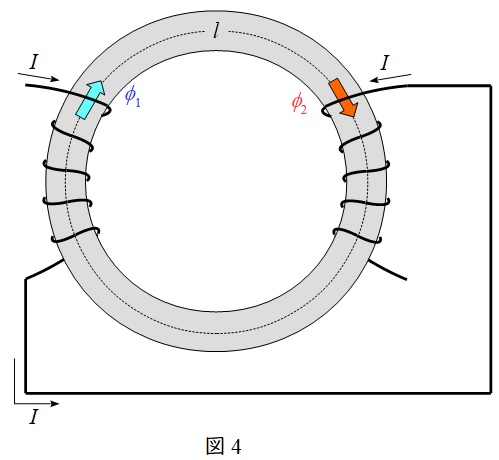
3.合成インダクタンス$ \ L_{0} \ $
自己インダクタンスが$ \ L_{1} \ \left[ \mathrm{H}\right] \ $と$ \ L_{2} \ \left[ \mathrm{H}\right] \ $を接続した時の合成インダクタンス$ \ L_{0} \ $は，相互インダクタンス$ \ M \ \left[ \mathrm{H}\right] \ $が与えられている時，以下の式で求められます。

①和動接続（磁束が強め合う）時(図4)
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}+2M \\[ 5pt ] \end{eqnarray}
\]

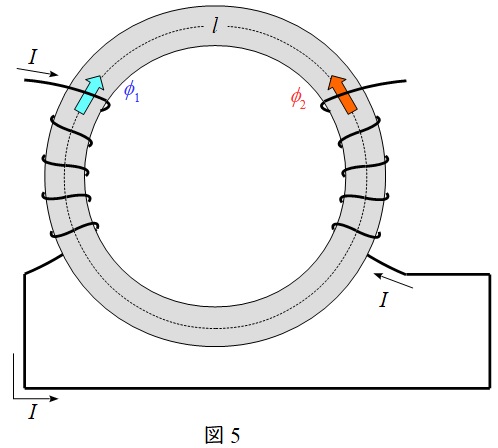
②差動接続（磁束が弱め合う）時(図5)
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}-2M \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ニ
ワンポイント解説「1.自己インダクタンスの定義$ \ L \ $」より，
\[
\begin{eqnarray}
L&=&\frac {N\phi }{I} \\[ 5pt ] \end{eqnarray}
\] であり，鉄心の磁束$ \ \phi \ $は磁路の断面積を$ \ S \ $，磁束密度を$ \ B \ $，磁路の長さを$ \ l \ $とすると，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&\mu HS \\[ 5pt ] &=&\frac {\mu NIS}{l} \\[ 5pt ] \end{eqnarray}
\] の関係があるため，
\[
\begin{eqnarray}
L&=&\frac {N\phi }{I} \\[ 5pt ] &=&\frac {N}{I}\times \frac {\mu NIS}{l} \\[ 5pt ] &=&\frac {\mu N^{2}S}{l} \\[ 5pt ] \end{eqnarray}
\] となり，自己インダクタンスは巻数$ \ N \ $の$ \ 2 \ $乗に比例する。したがって，コイル$ \ 1 \ $の巻数とコイル$ \ 2 \ $の巻線の比は$ \ 1 : a \ $であるため，コイル$ \ 1 \ $の自己インダクタンスを$ \ L_{1} \ $とすると，コイル$ \ 2 \ $の自己インダクタンス$ \ L_{2} \ $は，
\[
\begin{eqnarray}
\frac {L_{2}}{L_{1}}&=&\frac {N_{2}^{2}}{N_{1}^{2}} \\[ 5pt ] \frac {L_{2}}{L_{1}}&=&a^{2} \\[ 5pt ] L_{2}&=&a^{2}L_{1} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※　自己インダクタンスが巻数$ \ N \ $の$ \ 2 \ $乗に比例することは公式として覚えておいても良いです。

(2)解答：イ
本問においては，鉄心の内部にのみ磁界が発生するので結合係数$ \ k \ $は$ \ 1 \ $となる。したがって，相互インダクタンス$ \ M \ $は，ワンポイント解説「2.相互インダクタンス$ \ M \ $」の通り，
\[
\begin{eqnarray}
M&=&k\sqrt {L_{1}L_{2}} \\[ 5pt ] &=&1\times \sqrt {L_{1}\cdot a^{2}L_{1}} \\[ 5pt ] &=&aL_{1} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヲ
与えられた磁気エネルギーの式に，(1)解答式，(2)解答式及び$ \ I_{1}=-aI_{2} \ $を代入すると，
\[
\begin{eqnarray}
W&=&\frac {1}{2}L_{1}I_{1}^{2}+\frac {1}{2}L_{2}I_{2}^{2}+MI_{1}I_{2} \\[ 5pt ] &=&\frac {1}{2}L_{1}\left( -aI_{2}\right) ^{2}+\frac {1}{2}a^{2}L_{1}I_{2}^{2}+aL_{1}\left( -aI_{2}\right) I_{2} \\[ 5pt ] &=&\frac {1}{2}a^{2}L_{1}I_{2}^{2}+\frac {1}{2}a^{2}L_{1}I_{2}^{2}-a^{2}L_{1}I_{2}^{2} \\[ 5pt ] &=&0 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ホ
ワンポイント解説「3.合成インダクタンス$ \ L_{0} \ $」の通り，図1のコイル$ \ 1 \ $の端子$ \ \mathrm {b} \ $とコイル$ \ 2 \ $の端子$ \ \mathrm {c} \ $を接続した場合の接続は和動接続であるから，合成インダクタンス$ \ L_{0} \ $は，
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}+2M \\[ 5pt ] &=&L_{1}+a^{2}L_{1}+2aL_{1} \\[ 5pt ] &=&\left( a+1\right) ^{2}L_{1} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
図2においては相互インダクタンスがないので，合成インダクタンス$ \ L_{0}^{\prime } \ $は，
\[
\begin{eqnarray}
L_{0}^{\prime }&=&L_{1}+L_{2} \\[ 5pt ] &=&L_{1}+a^{2}L_{1} \\[ 5pt ] &=&\left( a^{2}+1\right) L_{1} \\[ 5pt ] \end{eqnarray}
\] と求められる。