《理論》〈電子理論〉[R03:問6]ホール効果測定のメカニズムに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，ホール効果測定に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

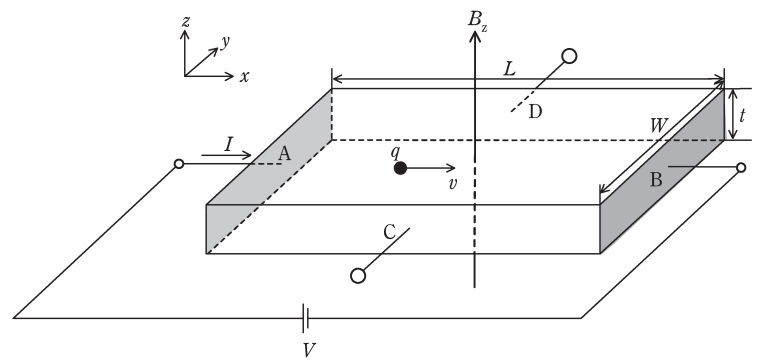
図のように，板状の半導体（長さ\( \ L \ \)，幅\( \ W \ \)，厚さ\( \ t \ \)）の\( \ \mathrm {A} \ \)面と\( \ \mathrm {B} \ \)面の間に電圧\( \ V\left( ＞0\right) \ \)を印加する。半導体中のキャリヤが電界から力を受けて一定速度\( \ v \ \)で運動している状況を考える。キャリヤが正の電荷量\( \ q \ \)を持つ正孔の場合，正孔の濃度を\( \ p \ \)，移動度を\( \ \mu _{\mathrm {h}} \ \)と仮定すると，運動の方向は\( \ x \ \)軸の正方向となり，\( \ v= \ \fbox {　 （１） 　} \ \)と表されることから，回路を流れる電流\( \ I \ \)は，\( \ I= \ \fbox {　 （２） 　} \ \)と表される。

この半導体に，図の\( \ z \ \)軸の正方向に磁束密度\( \ B_{\mathrm {z}}\left( ＞0\right) \ \)の磁界を印加すると，正孔がローレンツ力を受けることで，\( \ \mathrm {C} \ \)面の電位が\( \ \mathrm {D} \ \)面に対して\( \ \fbox {　 （３） 　} \ \)くなる。この電位差をホール電圧\( \ V_{\mathrm {H}} \ \)と定義する。定常状態では，\( \ V_{\mathrm {H}} \ \)による電界から受ける力と，ローレンツ力が釣り合うことから，\( \ V_{\mathrm {H}}= \ \fbox {　 （４） 　} \ \)と表される。以上の関係を用いると，\( \ V_{\mathrm {H}} \ \)と\( \ I \ \)を実測することにより\( \ \mu _{\mathrm {h}} \ \)と\( \ p \ \)が得られ，\( \ p= \ \fbox {　 （５） 　} \ \)と算出される。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　高　　　　　&（ロ）&　等し　　　　　&（ハ）&　\frac {\mu _{\mathrm {h}}V}{W} \\[ 5pt ] &（ニ）&　\frac {qp\mu _{\mathrm {h}}V}{L}　　　　　&（ホ）&　低　　　　　&（ヘ）&　\frac {qB_{\mathrm {z}}}{t}\frac {I}{V_{\mathrm {H}}} \\[ 5pt ] &（ト）&　\frac {\mu _{\mathrm {h}}V}{L}　　　　　&（チ）&　\frac {q\mu _{\mathrm {h}}VB_{\mathrm {z}}W}{L}　　　　　&（リ）&　\frac {\mu _{\mathrm {h}}VB_{\mathrm {z}}W}{L} \\[ 5pt ] &（ヌ）&　\frac {B_{\mathrm {z}}}{qt}\frac {I}{V_{\mathrm {H}}}　　　　　&（ル）&　\frac {B_{\mathrm {z}}}{qt}\frac {V_{\mathrm {H}}}{I}　　　　　&（ヲ）&　\frac {qp\mu _{\mathrm {h}}VtW}{L} \\[ 5pt ] &（ワ）&　\frac {qp\mu _{\mathrm {h}}VtL}{W}　　　　　 &（カ）&　\frac {\mu _{\mathrm {h}}L}{V}　　　　　 &（ヨ）&　\frac {\mu _{\mathrm {h}}VB_{\mathrm {z}}W}{Lt} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ホール効果測定に関する問題です。
ホール効果は半導体に電流を流し，さらに電流に直角の磁界をかけたとき，電流と磁界に直角の方向に電圧が生じる現象で，本問はそのメカニズムを説明している内容となっています。
電荷の偏りによる起電力の発生がポイントとなり，電子理論の範囲ですが電磁気の知識を使用する問題となります。

1.電界により電荷に働く力の大きさ
一様な電界\( \ E \ \)が電荷\( \ q \ \)にかかっているとき，この電荷\( \ q \ \)に働く力の大きさ\( \ F \ \)は，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] となります。

2.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \)，電子の速度\( \ v \ \)，電荷を\( \ q \ \)とすると，電荷にかかるローレンツ力\( \ F \ \)は，
\[
\begin{eqnarray}
F &=&qvB \\[ 5pt ] \end{eqnarray}
\] となります。

3.正孔と電子の移動度と電流密度
電界\( \ E \ \)が加わっている電界中に正孔と電子があるとすると，正孔は電界と同方向に，電子は電界と反対方向に動きます。その時の正孔と電子の速度を\( \ v_{\mathrm {h}} \ \)，\( \ v_{\mathrm {e}} \ \)，正孔と電子の移動度を\( \ \mu _{\mathrm {h}} \ \)，\( \ \mu_{\mathrm {e}} \ \)とすると，
\[
\begin{eqnarray}
v_{\mathrm {h}}&=&\mu _{\mathrm {h}}E \\[ 5pt ] v_{\mathrm {e}}&=&\mu _{\mathrm {e}}E \\[ 5pt ] \end{eqnarray}
\] の関係があります。ここで，正孔の電荷量が\( \ q \ \)，電子の電荷量が\( \ -q \ \)で，正孔と電子の濃度が\( \ p \ \)，\( \ n \ \)であるとすると，正孔と電子の電流密度\( \ J_{\mathrm {h}} \ \)，\( \ J_{\mathrm {e}} \ \)は，
\[
\begin{eqnarray}
J_{\mathrm {h}}&=&qpv_{\mathrm {h}} \\[ 5pt ] &=&qp\mu _{\mathrm {h}}E \\[ 5pt ] J_{\mathrm {e}}&=&-qnv_{\mathrm {e}} \\[ 5pt ] &=&-qn\mu _{\mathrm {e}}E \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ト
ワンポイント解説「3.正孔と電子の移動度と電流密度」の通り，正電荷の速度\( \ v \ \)は，電源\( \ V \ \)による電界を\( \ E \ \)とすると，
\[
\begin{eqnarray}
v&=&\mu _{\mathrm {h}}E \\[ 5pt ] &=&\frac {\mu _{\mathrm {h}}V}{L} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヲ
ワンポイント解説「3.正孔と電子の移動度と電流密度」の通り，半導体内の電流密度\( \ J \ \)は，
\[
\begin{eqnarray}
J&=&qpv \\[ 5pt ] &=&\frac {qp\mu _{\mathrm {h}}V}{L} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ \mathrm {A} \ \)面と\( \ \mathrm {B} \ \)面の面積\( \ S=Wt \ \)であるから，回路を流れる電流\( \ I \ \)は，
\[
\begin{eqnarray}
I&=&JS \\[ 5pt ] &=&\frac {qp\mu _{\mathrm {h}}V}{L}\cdot Wt \\[ 5pt ] &=&\frac {qp\mu _{\mathrm {h}}VtW}{L} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：イ
\( \ z \ \)軸の正方向に磁束密度\( \ B_{\mathrm {z}} \ \)が印加されると，ワンポイント解説「2.フレミングの左手の法則」の通り，図2のようにローレンツ力が加わる。すると，正電荷が\( \ \mathrm {C} \ \)面側に引き寄せられ，\( \ \mathrm {C} \ \)面の電位が\( \ \mathrm {D} \ \)面に対して高くなる。

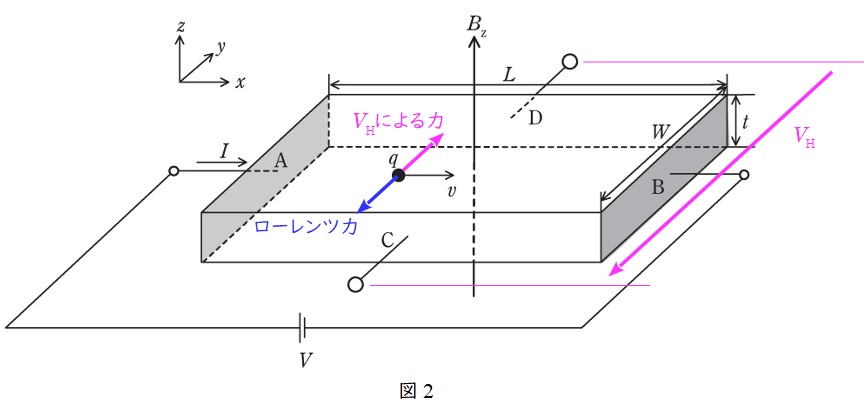
(4)解答：リ
\( \ V_{\mathrm {H}} \ \)による電界\( \ E_{\mathrm {H}} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {H}}&=&\frac {V_{\mathrm {H}}}{W} \\[ 5pt ] \end{eqnarray}
\] であり，その力の大きさ\( \ F_{\mathrm {H}} \ \)は，ワンポイント解説「1.電界により電荷に働く力の大きさ」の通り，
\[
\begin{eqnarray}
F_{\mathrm {H}}&=&qE_{\mathrm {H}} \\[ 5pt ] &=&\frac {qV_{\mathrm {H}}}{W} \\[ 5pt ] \end{eqnarray}
\] となる。定常状態においては，ローレンツ力と等しいので，
\[
\begin{eqnarray}
F_{\mathrm {H}}=\frac {qV_{\mathrm {H}}}{W}&=&qvB_{\mathrm {z}} \\[ 5pt ] \frac {qV_{\mathrm {H}}}{W}&=&q\cdot \frac {\mu _{\mathrm {h}}V}{L}\cdot B_{\mathrm {z}} \\[ 5pt ] \frac {V_{\mathrm {H}}}{W}&=&\frac {\mu _{\mathrm {h}}VB_{\mathrm {z}}}{L} \\[ 5pt ] V_{\mathrm {H}}&=&\frac {\mu _{\mathrm {h}}VB_{\mathrm {z}}W}{L} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
(2)，(4)解答式より，
\[
\begin{eqnarray}
\frac {\mu _{\mathrm {h}}VW}{L}=\frac {I}{qpt}&=&\frac {V_{\mathrm {H}}}{B_{\mathrm {z}}} \\[ 5pt ] \end{eqnarray}
\] となるから，これを\( \ p \ \)について整理すると，
\[
\begin{eqnarray}
\frac {I}{qpt}&=&\frac {V_{\mathrm {H}}}{B_{\mathrm {z}}} \\[ 5pt ] p&=&\frac {B_{\mathrm {z}}}{qt}\frac {I}{V_{\mathrm {H}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。