【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,分布定数回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
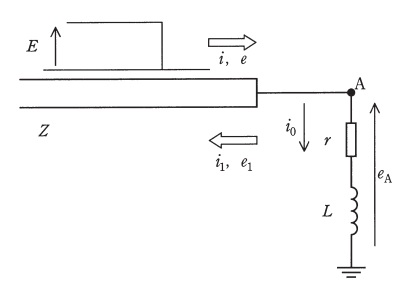
図のように特性インピーダンスが\( \ Z \ \)の半無限長無損失線路の終端\( \ \mathrm {A} \ \)に,負荷として抵抗\( \ r \ \)とインダクタンス\( \ L \ \)のコイルが接続されている。
波頭がステップ状で波高値\( \ E \ \)の電圧波\( \ e \ \)と,それに伴い波高値\( \ I \ \)の電流\( \ i \ \)が図の左側から終端\( \ \mathrm {A} \ \)に向かって入射した。入射波は時刻\( \ t=0 \ \)のときに終端\( \ \mathrm {A} \ \)に達した。このときの終端\( \ \mathrm {A} \ \)での電流\( \ i \ \)と反射による電流\( \ i_{1} \ \)及び負荷に流れる電流\( \ i_{0} \ \)との関係及び負荷の両端の電圧\( \ e_{\mathrm {A}} \ \)を求めたい。電流\( \ i_{1} \ \),電流\( \ i_{0} \ \)及び電圧\( \ e_{\mathrm {A}} \ \),終端\( \ \mathrm {A} \ \)での反射により生じる電圧\( \ e_{1} \ \)を図のようにとる。電流は入射波が終端\( \ \mathrm {A} \ \)に向かって進行する方向を正とする。
入射波到達後において,終端\( \ \mathrm {A} \ \)での電圧,電流の関係は次式で表される。
\[
\begin{eqnarray}
&&e + e_{1} = Zi+\left( -Zi_{1}\right) = e_{\mathrm {A}} \\[ 5pt ]
&&i + i_{1} = i_{0}
\end{eqnarray}
\]
\( \ e_{\mathrm {A}} \ \)と\( \ i_{0} \ \)の関係は次式で表される。
\[
e_{\mathrm {A}}=\fbox { (1) }
\]
これらの式より,\( \ i_{0} \ \)の時間的変化を表す微分方程式が得られる。この式を初期値を考慮して解くと,
\[
i_{0}=\fbox { (2) }
\]
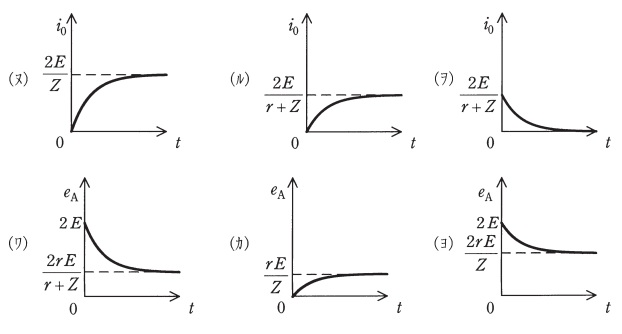
となり,時間的変化を表す図は\( \ \fbox { (3) } \ \)である。
また,\( \ e_{\mathrm {A}} \ \)を\( \ E \ \)を用いて表すと次式となり,
\[
e_{\mathrm {A}}=\fbox { (4) }
\]
その時間的変化を表す図は\( \ \fbox { (5) } \ \)である。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {2E}{r+Z}\left( 1-\mathrm {e}^{-\frac {r+Z}{L}t}\right) &(ロ)& \frac {2E}{r+Z}\left[ r+Z\mathrm {e}^{-\left( r+Z\right) Lt}\right] &(ハ)& L\frac {\mathrm {d}i_{0}}{\mathrm {d}t}+ri_{0} \\[ 5pt ]
&(ニ)& 2E\left( \frac {r}{Z}+\mathrm {e}^{-\frac {r+Z}{L}t}\right) &(ホ)& \frac {2E}{r+Z}\left( r+Z\mathrm {e}^{-\frac {r+Z}{L}t}\right) &(ヘ)& L\frac {\mathrm {d}i_{0}}{\mathrm {d}t} \\[ 5pt ]
&(ト)& \frac {2E}{Z}\left( 1-\mathrm {e}^{-\frac {r+Z}{L}t}\right) &(チ)& \frac {2E}{r+Z}\left[ 1-\mathrm {e}^{-\left( r+Z\right) Lt}\right] &(リ)& \frac {1}{L}\frac {\mathrm {d}i_{0}}{\mathrm {d}t}+ri_{0} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電験一種では分布定数回路の問題が高い頻度で出題されます。本問は分布定数回路の電圧の電流の式が与えられているので,(2)の連立方程式と微分方程式の問題が解けるかどうかが肝となりそうです。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ V_{\mathrm {R}} \ \),リアクトル\( \ L \ \)の電圧\( \ V_{\mathrm {L}} \ \),コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm {C}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm {R}} &=& Ri \\[ 5pt ]
V_{\mathrm {L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm {C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解すなわち\( \ L \ \)開放(\( \ E=0 \ \)と同義)の時の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\frac {\mathrm {d}y}{\mathrm {d}x} \ln {x} =\frac {1}{x}
\]
②自然対数の積分
\[
\int \frac {1}{x}\mathrm {d}x =\ln {x} + C \left( Cは積分定数\right)
\]
\[
\ln {x}=-\alpha t +C \left( Cは積分定数\right)の時, x=A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right)となります。
\]
【解答】
(1)解答:ハ
ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」より,\( \ \mathrm {A} \ \)から抵抗\( \ r \ \)とインダクタンス\( \ L \ \)側の回路にキルヒホッフの法則を適用すると,
\[
e_{\mathrm {A}}=L\frac {\mathrm {d}i_{0}}{\mathrm {d}t}+ri_{0}
\]
と求められる。
(2)解答:イ
題意より,
\[
\begin{eqnarray}
&&e + e_{1} = Zi+\left( -Zi_{1}\right) = e_{\mathrm {A}}& ・・・・・・・・・・①& \\[ 5pt ]
&&i + i_{1} = i_{0}& ・・・・・・・・・・②& \\[ 5pt ]
&&e=E& ・・・・・・・・・・③& \\[ 5pt ]
&&i=I=\frac {E}{Z}& ・・・・・・・・・・④&
\end{eqnarray}
\]
である。②,④より,
\[
\begin{eqnarray}
i + i_{1} &=& i_{0} \\[ 5pt ]
i_{1} &=& i_{0}-i \\[ 5pt ]
i_{1} &=& i_{0}-\frac {E}{Z} \\[ 5pt ]
e_{1}=-Zi_{1} &=& E-Zi_{0}
\end{eqnarray}
\]
であるから,これと③を①に代入すると,
\[
\begin{eqnarray}
e + e_{1} &=& e_{\mathrm {A}} \\[ 5pt ]
E + E-Zi_{0} &=& e_{\mathrm {A}}\\[ 5pt ]
2E-Zi_{0} &=& e_{\mathrm {A}}
\end{eqnarray}
\]
となるので,これを(1)解答式に代入すると,
\[
\begin{eqnarray}
e_{\mathrm {A}}&=&L\frac {\mathrm {d}i_{0}}{\mathrm {d}t}+ri_{0} \\[ 5pt ]
2E-Zi_{0} &=& L\frac {\mathrm {d}i_{0}}{\mathrm {d}t}+ri_{0} \\[ 5pt ]
L\frac {\mathrm {d}i_{0}}{\mathrm {d}t}+\left( r+Z\right) i_{0} &=& 2E
\end{eqnarray}
\]
と回路方程式が導出される。これをワンポイント解説「2.過渡現象における定常解と過渡解」に沿って.定常解を\( \ i_{\mathrm {0s}} \ \),過渡解を\( \ i_{\mathrm {0t}} \ \)とすると,定常解を\( \ i_{\mathrm {0s}} \ \)は,
\[
\begin{eqnarray}
\left( r+Z\right) i_{\mathrm {0s}} &=& 2E \\[ 5pt ]
i_{\mathrm {0s}} &=& \frac {2E}{r+Z}
\end{eqnarray}
\]
過渡解\( \ i_{\mathrm {0t}} \ \)は,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{\mathrm {0t}}}{\mathrm {d}t}+\left( r+Z\right) i_{\mathrm {0t}} &=& 0 \\[ 5pt ]
L\frac {\mathrm {d}i_{\mathrm {0t}}}{\mathrm {d}t} &=& -\left( r+Z\right) i_{\mathrm {0t}} \\[ 5pt ]
\frac {1}{i_{\mathrm {0t}}} \mathrm {d}i_{\mathrm {0t}} &=& -\frac {r+Z}{L} \mathrm {d}t
\end{eqnarray}
\]
両辺を積分すると,
\[
\begin{eqnarray}
\int \frac {1}{i_{\mathrm {0t}}} \mathrm {d}i_{\mathrm {0t}} &=& \int -\frac {r+Z}{L} \mathrm {d}t \\[ 5pt ]
\ln \ {i_{\mathrm {0t}}} &=& -\frac {r+Z}{L} t+C \left( Cは積分定数\right) \\[ 5pt ]
i_{\mathrm {0t}} &=& A\mathrm {e}^{-\frac {r+Z}{L} t} \left( A=\mathrm {e}^{C}\right)
\end{eqnarray}
\]
と求められる。よって,一般解\( \ i_{0} \ \)は,
\[
\begin{eqnarray}
i_{0} &=& i_{\mathrm {0s}}+i_{\mathrm {0t}} \\[ 5pt ]
&=& \frac {2E}{r+Z}+A\mathrm {e}^{-\frac {r+Z}{L} t}
\end{eqnarray}
\]
となり,初期値が零であるから,\( \ t=0 \ \)の時,\( \ i_{0}=0 \ \)となるので,
\[
\begin{eqnarray}
0 &=& \frac {2E}{r+Z}+A \\[ 5pt ]
A &=& -\frac {2E}{r+Z}
\end{eqnarray}
\]
となり,一般解は,
\[
\begin{eqnarray}
i_{0} &=& \frac {2E}{r+Z}-\frac {2E}{r+Z}\mathrm {e}^{-\frac {r+Z}{L} t} \\[ 5pt ]
&=& \frac {2E}{r+Z}\left( 1-\mathrm {e}^{-\frac {r+Z}{L}t}\right)
\end{eqnarray}
\]
と求められる。
(3)解答:ル
\( \ i_{0}\left( 0\right) =0 \ \)及び(2)の解答式より
\[
\begin{eqnarray}
i_{0}\left( \infty \right) &=& \displaystyle \lim_{ t \to \infty } \left[ \frac {2E}{r+Z}\left( 1-\mathrm {e}^{-\frac {r+Z}{L}t}\right) \right] \\[ 5pt ]
&=& \frac {2E}{r+Z}
\end{eqnarray}
\]
であるから,これを満たすグラフは(ル)となる。
(4)解答:ホ
(2)解答式より,
\[
\begin{eqnarray}
\frac {\mathrm {d}i_{0}}{\mathrm {d}t} &=& \frac {\mathrm {d}}{\mathrm {d}t}\left[ \frac {2E}{r+Z}\left( 1-\mathrm {e}^{-\frac {r+Z}{L}t}\right) \right] \\[ 5pt ]
&=& \frac {2E}{r+Z}\left( \frac {r+Z}{L}\mathrm {e}^{-\frac {r+Z}{L}t}\right) \\[ 5pt ]
&=& \frac {2E}{L}\mathrm {e}^{-\frac {r+Z}{L}t}
\end{eqnarray}
\]
であるから,これと(2)解答式を(1)解答式に代入すると,
\[
\begin{eqnarray}
e_{\mathrm {A}} &=& L\frac {\mathrm {d}i_{0}}{\mathrm {d}t}+ri_{0} \\[ 5pt ]
&=& L\frac {2E}{L}\mathrm {e}^{-\frac {r+Z}{L}t}+r\frac {2E}{r+Z}\left( 1-\mathrm {e}^{-\frac {r+Z}{L}t}\right) \\[ 5pt ]
&=& \frac {2E}{r+Z}\left[ \left(r+Z\right) \mathrm {e}^{-\frac {r+Z}{L}t} +r\left( 1-\mathrm {e}^{-\frac {r+Z}{L}t}\right) \right] \\[ 5pt ]
&=& \frac {2E}{r+Z}\left( r+Z\mathrm {e}^{-\frac {r+Z}{L}t}\right)
\end{eqnarray}
\]
と求められる。
(5)解答:ワ
(4)の解答式より,
\[
\begin{eqnarray}
e_{\mathrm {A}}\left( 0\right) &=& \frac {2E}{r+Z}\left( r+Z\mathrm {e}^{-\frac {r+Z}{L}\times 0}\right) \\[ 5pt ]
&=& 2E \\[ 5pt ]
e_{\mathrm {A}}\left( \infty \right)&=& \displaystyle \lim_{ t \to \infty } \left[ \frac {2E}{r+Z}\left( r+Z\mathrm {e}^{-\frac {r+Z}{L}t}\right) \right] \\[ 5pt ]
&=& \frac {2rE}{r+Z}
\end{eqnarray}
\]
となるので,これを満たすグラフは(ワ)となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん