【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,電気回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
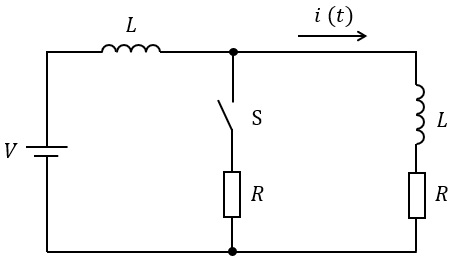
図の回路は,電圧\( \ V \ \)の直流電圧源,スイッチ\( \ \mathrm {S} \ \),抵抗\( \ R \ \)及びインダクタンス\( \ L \ \)のインダクタから構成されており,二つのインダクタ間には相互誘導はないものとする。
時刻\( \ t < 0 \ \)ではスイッチ\( \ \mathrm {S} \ \)は閉じており,回路は定常状態にある。\( \ t = 0 \ \)でスイッチ\( \ \mathrm {S} \ \)を開くこととする。\( \ t ≧ 0 \ \)における回路の電流を\( \ i (t) \ \)とすれば,\( \ t ≧ 0 \ \)において次式の回路方程式が成り立つ。
\[
\begin{eqnarray}
\ \fbox { (1) } \ &=& V ・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
スイッチ\( \ \mathrm {S} \ \)を開く直前と直後において二つのインダクタによる磁束の和は不変であるので,スイッチ\( \ \mathrm {S} \ \)を開いた直後の電流を\( \ i (0) \ \)とすれば,スイッチ\( \ \mathrm {S} \ \)を開く直前と直後における二つのインダクタによる磁束に関して次式が成り立つ。
\[
\begin{eqnarray}
\ \fbox { (2) } \ &=& 2Li (0) \\[ 5pt ]
\end{eqnarray}
\]
また,①式の回路方程式の定常解を\( \ i_{\mathrm {S}} (t) \ \),過渡解を\( \ i_{\mathrm {T}} (t) \ \)とすれば,\( \ K \ \)を任意定数として,
\[
\begin{eqnarray}
i_{\mathrm {S}} (t) &=& \ \fbox { (3) } \\[ 5pt ]
i_{\mathrm {T}} (t) &=& \ \fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
となる。
回路方程式の定常解\( \ i_{\mathrm {S}} (t) \ \)と過渡解\( \ i_{\mathrm {T}} (t) \ \),及びスイッチ\( \ \mathrm {S} \ \)を開いた直後の電流\( \ i (0) \ \)の条件より,\( \ t ≧ 0 \ \)における\( \ i (t) \ \)は次式となる。
\[
\begin{eqnarray}
i (t) &=& \ \fbox { (5) } \\[ 5pt ]
\end{eqnarray}
\]
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {2LV}{R} &(ロ)& \frac {V}{2R}+\frac {V}{R}\mathrm {e}^{-\frac {2R}{L}t} &(ハ)& \frac {V}{R}-\frac {V}{2R}\mathrm {e}^{-\frac {R}{2L}t} \\[ 5pt ]
&(ニ)& L\frac {\mathrm {d}i (t)}{\mathrm {d}t}+2Ri (t) &(ホ)& \frac {2V}{R} &(ヘ)& \frac {V}{R} \\[ 5pt ]
&(ト)& K\mathrm {e}^{-\frac {R}{2L}t} &(チ)& K\mathrm {e}^{-\frac {R}{L}t} &(リ)& \frac {3LV}{R} \\[ 5pt ]
&(ヌ)& L\frac {\mathrm {d}i (t)}{\mathrm {d}t}+Ri (t) &(ル)& 2L\frac {\mathrm {d}i (t)}{\mathrm {d}t}+Ri (t) &(ヲ)& \frac {V}{R}+\frac {V}{2R}\mathrm {e}^{-\frac {R}{2L}t} \\[ 5pt ]
&(ワ)& K\mathrm {e}^{-\frac {2R}{L}t} &(カ)& \frac {V}{2R} &(ヨ)& \frac {LV}{R} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
抵抗とインダクタンスが直並列された回路の過渡現象を求める問題です。
おそらく(2)の初期条件の導出が少し迷う問題ですが,\( \ 1 \ \)種としては比較的オーソドックスな過渡現象の問題と言えると思います。ぜひ完答を目指していくようにして下さい。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \mathrm {[A]} \ \)とし,抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の電圧\( \ V_{\mathrm{R}} \ \mathrm {[V]} \ \),リアクトル\( \ L \ \mathrm {[H]} \ \)の電圧\( \ V_{\mathrm{L}} \ \mathrm {[V]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)の電圧\( \ V_{\mathrm{C}} \ \mathrm {[V]} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t =\frac {q}{C}\\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left ( \ln {x} \right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x&=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時, x=A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right)となります。 \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ル
スイッチ\( \ \mathrm {S} \ \)を開いた後,回路のインダクタンスは\( \ 2L \ \),抵抗は\( \ R \ \)であるから,回路方程式は,
\[
\begin{eqnarray}
2L\frac {\mathrm {d}i (t)}{\mathrm {d}t}+Ri (t) &=&V \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:リ
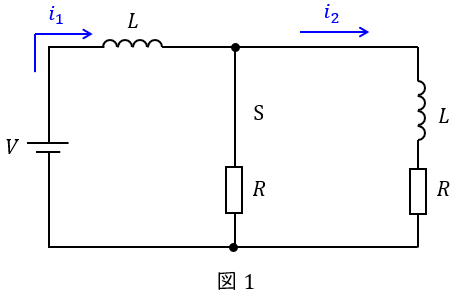
\( \ t = 0 \ \)でスイッチ\( \ \mathrm {S} \ \)を開く前の回路は図1のようになる。このとき,各インダクタに流れる電流を\( \ i_{1} \ \)及び\( \ i_{2} \ \)とする。
定常状態においてはインダクタは短絡と考えれば良いので,定常状態における回路の合成抵抗は\( \ \displaystyle \frac {R}{2} \ \)であるから,
\[
\begin{eqnarray}
i_{1} &=&\frac {V}{\displaystyle \frac {R}{2}} \\[ 5pt ]
&=&\frac {2V}{R} \\[ 5pt ]
\end{eqnarray}
\]
となり,分流の法則より\( \ i_{2} \ \)は,
\[
\begin{eqnarray}
i_{2} &=&\frac {R}{R+R}i_{1} \\[ 5pt ]
&=&\frac {1}{2}\times \frac {2V}{R} \\[ 5pt ]
&=&\frac {V}{R} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,インダクタの磁束と電流の関係\( \ N\phi =LI \ \)より,スイッチ\( \ \mathrm {S} \ \)を開く直前における二つのインダクタによる磁束は,
\[
\begin{eqnarray}
Li_{1}+Li_{2} &=&L\frac {2V}{R}+L\frac {V}{R} \\[ 5pt ]
&=&\frac {3LV}{R}\\[ 5pt ]
\end{eqnarray}
\]
となり,スイッチ\( \ \mathrm {S} \ \)を開く直前と直後における二つのインダクタによる磁束に関して,
\[
\begin{eqnarray}
\frac {3LV}{R} &=& 2Li (0) \\[ 5pt ]
\end{eqnarray}
\]
の関係が成り立つ。
(3)解答:ヘ
①について,定常解\( \ i_{\mathrm {S}} (t) \ \)は\( \ \displaystyle \frac {\mathrm {d}i (t)}{\mathrm {d}t}=0 \ \)であるから,
\[
\begin{eqnarray}
Ri_{\mathrm {S}} (t) &=&V \\[ 5pt ]
i_{\mathrm {S}} (t) &=&\frac {V}{R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ト
過渡解\( \ i_{\mathrm {T}} (t) \ \)については,\( \ V=0 \ \)とすれば,
\[
\begin{eqnarray}
2L\frac {\mathrm {d}i_{\mathrm {T}} (t)}{\mathrm {d}t}+Ri_{\mathrm {T}} (t) &=&0 \\[ 5pt ]
2L\frac {\mathrm {d}i_{\mathrm {T}} (t)}{\mathrm {d}t}&=&-Ri_{\mathrm {T}} (t) \\[ 5pt ]
\frac {1}{i_{\mathrm {T}} (t)}\mathrm {d}i_{\mathrm {T}} (t)&=&-\frac {R}{2L}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺積分すると,
\[
\begin{eqnarray}
\int \frac {1}{i_{\mathrm {T}} (t)}\mathrm {d}i_{\mathrm {T}} (t)&=&\int -\frac {R}{2L}\mathrm {d}t \\[ 5pt ]
\ln i_{\mathrm {T}} (t)&=&-\frac {R}{2L}t+C ( \ C \ は積分定数) \\[ 5pt ]
i_{\mathrm {T}} (t)&=&K\mathrm {e}^{-\frac {R}{2L}t} ( \ K \ は積分定数) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
(3)及び(4)より一般解\( \ i (t) \ \)は,
\[
\begin{eqnarray}
i (t)&=&i_{\mathrm {S}} (t)+i_{\mathrm {T}} (t) \\[ 5pt ]
&=&\frac {V}{R}+K\mathrm {e}^{-\frac {R}{2L}t} \\[ 5pt ]
\end{eqnarray}
\]
となり,(2)解答式より初期条件\( \ i (0) \ \)は,
\[
\begin{eqnarray}
\frac {3LV}{R} &=& 2Li (0) \\[ 5pt ]
i (0) &=&\frac {3V}{2R} \\[ 5pt ]
\end{eqnarray}
\]
であるから,積分定数\( \ K \ \)は,
\[
\begin{eqnarray}
\frac {3V}{2R}&=&\frac {V}{R}+K\mathrm {e}^{-\frac {R}{2L}\times 0} \\[ 5pt ]
\frac {3V}{2R}&=&\frac {V}{R}+K \\[ 5pt ]
K&=&\frac {V}{2R} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,\( \ t ≧ 0 \ \)における\( \ i (t) \ \)は,
\[
\begin{eqnarray}
i (t)&=&\frac {V}{R}+\frac {V}{2R}\mathrm {e}^{-\frac {R}{2L}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん