【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。ただし,\( \ a \ \)は複素数で\( \ a=e^{\mathrm {j}\frac {2}{3}\pi } \ \)とする。
図1のように対称三相交流電圧源に\( \ \mathrm {Y} \ \)形不平衡負荷を接続した。
\( \ {\dot E}_{\mathrm {a}}=120 \ \mathrm {V}∠0° \ \)であり,相回転は\( \ {\dot E}_{\mathrm {a}} \ \),\( \ {\dot E}_{\mathrm {b}} \ \),\( \ {\dot E}_{\mathrm {c}} \ \)の順とする。この相回転の順を式で表すと
\[
\begin{eqnarray}
{\dot E}_{\mathrm {b}} &=& a^{2}{\dot E}_{\mathrm {a}},{\dot E}_{\mathrm {c}} &=& a{\dot E}_{\mathrm {a}} ・・・・・・・・・・① \\[ 5pt ]
\end{eqnarray}
\]
となる。いま,回路の線電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)も対称三相であり,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b}} &=& a^{2}{\dot I}_{\mathrm {a}},{\dot I}_{\mathrm {c}} &=& a{\dot I}_{\mathrm {a}} ・・・・・・・・・・② \\[ 5pt ]
\end{eqnarray}
\]
の関係式を満たしているものとする。このとき,\( \ \mathrm {Y} \ \)形不平衡負荷の各相の電圧平衡の式は
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}{\dot Z}_{\mathrm {a}} &=& {\dot E}_{\mathrm {a}}-\fbox { (1) },{\dot I}_{\mathrm {b}}{\dot Z}_{\mathrm {b}} &=& {\dot E}_{\mathrm {b}}-\fbox { (1) },{\dot I}_{\mathrm {c}}{\dot Z}_{\mathrm {c}} &=& {\dot E}_{\mathrm {c}}-\fbox { (1) }・・③ \\[ 5pt ]
\end{eqnarray}
\]
であるから,①式と②式を利用すると,③式より\( \ \mathrm {Y} \ \)形不平衡負荷のインピーダンスは
\[
\begin{pmatrix}
{\dot Z}_{\mathrm {a}} \\ {\dot Z}_{\mathrm {b}} \\ {\dot Z}_{\mathrm {c}}
\end{pmatrix}
=
\begin{pmatrix}
1 \\ 1 \\ 1
\end{pmatrix}
\frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-\fbox { (2) }\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} ・・・④ \\[ 5pt ]
\]
と表すことができる。ただし,\( \ a^{3}=1 \ \)に注意する。
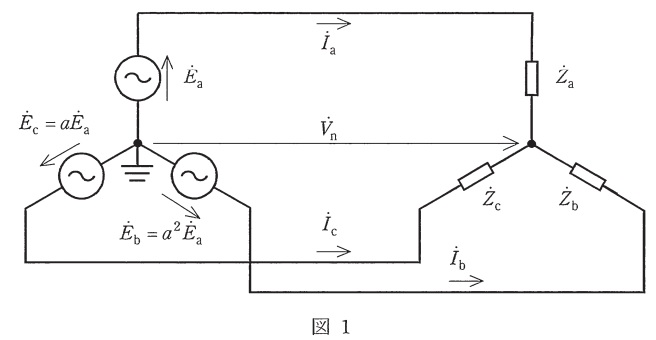
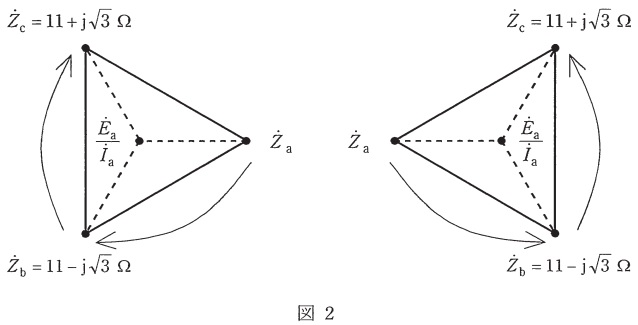
ここで,①式と②式が成立して,\( \ {\dot Z}_{\mathrm {b}}=11-\mathrm {j}\sqrt {3} \ \Omega ,{\dot Z}_{\mathrm {c}}=11+\mathrm {j}\sqrt {3} \ \Omega \ \)であるときを考える。④式に従って\( \ {\dot Z}_{\mathrm {a}} \ \),\( \ {\dot Z}_{\mathrm {b}} \ \),\( \ {\dot Z}_{\mathrm {c}} \ \)を複素平面上にプロットすると,これらは中心が\( \ \displaystyle \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}} \ \)である正三角形の頂点をなし,図2のどちらかになる。なお,\( \ {\dot Z}_{\mathrm {a}} \ \)と\( \ \displaystyle \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}} \ \)は実軸上に位置している。図2の二つの三角形のうち,④式と整合する正三角形を利用すると\( \ {\dot Z}_{\mathrm {a}}= \ \fbox { (3) } \ \Omega \ \),\( \ {\dot I}_{\mathrm {a}}= \ \fbox { (4) } \ \mathrm {A} \ \),\( \ {\dot V}_{\mathrm {n}}= \ \fbox { (5) }\mathrm {V} \ \)であることが分かる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& a^{2}{\dot V}_{\mathrm {n}} &(ロ)& 14 &(ハ)& 13 \\[ 5pt ]
&(ニ)& 16 &(ホ)& 8 &(ヘ)& 24 \\[ 5pt ]
&(ト)& {\dot V}_{\mathrm {n}} &(チ)& a{\dot V}_{\mathrm {n}} &(リ)& 32 \\[ 5pt ]
&(ヌ)& -20 &(ル)& 12 &(ヲ)& 10 \\[ 5pt ]
&(ワ)& \begin{pmatrix}
1 \\ a \\ a^{2}
\end{pmatrix} &(カ)& \begin{pmatrix}
1 \\ a^{2} \\ a
\end{pmatrix} &(ヨ)& \begin{pmatrix}
a \\ a^{2} \\ 1
\end{pmatrix}
\end{eqnarray}
\]
【ワンポイント解説】
三相交流回路の問題は電験一種問5の定番問題となっています。この問題は\( \ \Delta -\mathrm {Y} \ \)変換等もなく,複雑な計算もないので,例年に比べれば易しめの問題と言えると思います。
1.ベクトルオペレータ\( \ a \ \)
題意で与えられているベクトルオペレータ\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)は,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} &=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} &=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} &=& 1
\end{eqnarray}
\]
となります。したがって,
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ]
\overline {a^{2}} &=& a \\[ 5pt ]
1+a+a^{2} &=& 0
\end{eqnarray}
\]
が成立します。
【解答】
(1)解答:ト
図1より,\( \ {\dot E}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot Z}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {n}} \ \)の関係は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {a}}-{\dot Z}_{\mathrm {a}}{\dot I}_{\mathrm {a}} &=& {\dot V}_{\mathrm {n}} \\[ 5pt ]
{\dot Z}_{\mathrm {a}}{\dot I}_{\mathrm {a}} &=& {\dot E}_{\mathrm {a}}-{\dot V}_{\mathrm {n}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。同様に,\( \ \mathrm {b} \ \)相,\( \ \mathrm {c} \ \)相も
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {b}}{\dot I}_{\mathrm {b}} &=& {\dot E}_{\mathrm {b}}-{\dot V}_{\mathrm {n}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}{\dot I}_{\mathrm {c}} &=& {\dot E}_{\mathrm {c}}-{\dot V}_{\mathrm {n}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ワ
(1)より,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}{\dot I}_{\mathrm {a}} &=& {\dot E}_{\mathrm {a}}-{\dot V}_{\mathrm {n}} \\[ 5pt ]
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {b}}{\dot I}_{\mathrm {b}} &=& {\dot E}_{\mathrm {b}}-{\dot V}_{\mathrm {n}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}} &=& \frac {{\dot E}_{\mathrm {b}}}{{\dot I}_{\mathrm {b}}}-\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {b}}} \\[ 5pt ]
&=& \frac {a^{2}{\dot E}_{\mathrm {a}}}{a^{2}{\dot I}_{\mathrm {a}}}-\frac {{\dot V}_{\mathrm {n}}}{a^{2}{\dot I}_{\mathrm {a}}} \\[ 5pt ]
&=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-\frac {a^{3}{\dot V}_{\mathrm {n}}}{a^{2}{\dot I}_{\mathrm {a}}} \left( ∵ a^{3}=1\right) \\[ 5pt ]
&=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-a\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {c}}{\dot I}_{\mathrm {c}} &=& {\dot E}_{\mathrm {c}}-{\dot V}_{\mathrm {n}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}} &=& \frac {{\dot E}_{\mathrm {c}}}{{\dot I}_{\mathrm {c}}}-\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {c}}} \\[ 5pt ]
&=& \frac {a{\dot E}_{\mathrm {a}}}{a{\dot I}_{\mathrm {a}}}-\frac {{\dot V}_{\mathrm {n}}}{a{\dot I}_{\mathrm {a}}} \\[ 5pt ]
&=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-\frac {a^{3}{\dot V}_{\mathrm {n}}}{a{\dot I}_{\mathrm {a}}} \left( ∵ a^{3}=1\right) \\[ 5pt ]
&=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-a^{2}\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{pmatrix}
{\dot Z}_{\mathrm {a}} \\ {\dot Z}_{\mathrm {b}} \\ {\dot Z}_{\mathrm {c}}
\end{pmatrix}
=
\begin{pmatrix}
1 \\ 1 \\ 1
\end{pmatrix}
\frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-
\begin{pmatrix}
1 \\ a \\ a^{2}
\end{pmatrix}\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
\]
と求められる。
(3)解答:ホ
まず図2の左側の正三角形であると仮定すると,各線分の長さは図2-1の赤字で示されている長さとなるため,
\[
\begin{eqnarray}
\frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}&=& 12 \\[ 5pt ]
{\dot Z}_{\mathrm {a}} &=& 14 \\[ 5pt ]
\end{eqnarray}
\]
となる。これを(2)の解答式に代入すると,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
14&=&12-\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}}&=&-2 \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ {\dot Z}_{\mathrm {b}} \ \),\( \ {\dot Z}_{\mathrm {c}} \ \)を求めると,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {b}} &=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-a\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
&=& 12+2a \\[ 5pt ]
&=& 11+\mathrm {j}\sqrt{3} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {c}} &=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-a^{2}\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
&=& 12+2a^{2} \\[ 5pt ]
&=& 11-\mathrm {j}\sqrt{3} \\[ 5pt ]
\end{eqnarray}
\]
となるので,図2-1と合致しない。
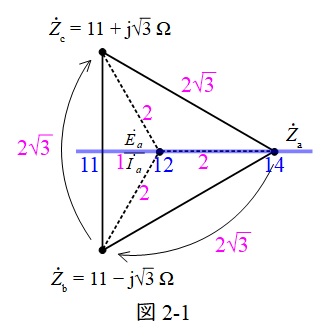
次に,図2の右側であるとすると,各線分の長さは図2-2の赤字で示されている長さとなるため,
\[
\begin{eqnarray}
\frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}&=& 10 \\[ 5pt ]
{\dot Z}_{\mathrm {a}} &=& 8 \\[ 5pt ]
\end{eqnarray}
\]
となる。これを(2)の解答式に代入すると,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
8&=&10-\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}}&=&2 \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ {\dot Z}_{\mathrm {b}} \ \),\( \ {\dot Z}_{\mathrm {c}} \ \)を求めると,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {b}} &=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-a\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
&=& 10-2a \\[ 5pt ]
&=& 11-\mathrm {j}\sqrt{3} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {c}} &=& \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}-a^{2}\frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}} \\[ 5pt ]
&=& 10-2a^{2} \\[ 5pt ]
&=& 11+\mathrm {j}\sqrt{3} \\[ 5pt ]
\end{eqnarray}
\]
となるので,図2-2と合致する。よって,こちらの三角形が整合する三角形となる。よって,\({\dot Z}_{\mathrm {a}}=8 \ \Omega \)となる。
(4)解答:ル
\( \ \displaystyle \frac {{\dot E}_{\mathrm {a}}}{{\dot I}_{\mathrm {a}}}= 10 \ \),\( \ {\dot E}_{\mathrm {a}}=120 \ \mathrm {V} \ \)であるので,\( \ {\dot I}_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
\frac {120}{{\dot I}_{\mathrm {a}}} &=& 10\\[ 5pt ]
{\dot I}_{\mathrm {a}}&=&12 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヘ
(4)より,\( \ \displaystyle \frac {{\dot V}_{\mathrm {n}}}{{\dot I}_{\mathrm {a}}}=2 \ \)であるので,
\[
\begin{eqnarray}
\frac {{\dot V}_{\mathrm {n}}}{12} &=& 2\\[ 5pt ]
{\dot V}_{\mathrm {n}}&=&24 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん