【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,図の三相交流回路に関する記述である。負荷や再生可能エネルギー電源などに設置された電力変換器から高調波電流が発生すると電圧ひずみが発生する。二次系統など中性点の接地された回路でこの電圧ひずみを計算したい。基本波の角周波数を\( \ \omega \ \)として,文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
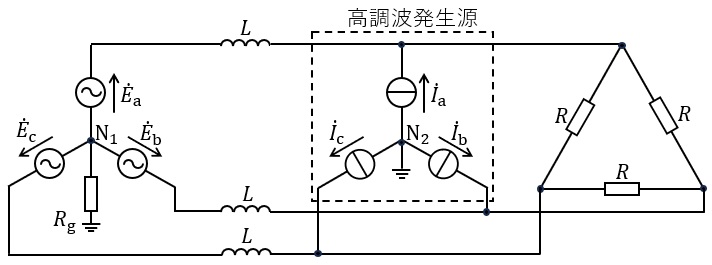
図のように,対称三相交流電圧源\( \ {\dot E}_{\mathrm {a}} \ \),\( \ {\dot E}_{\mathrm {b}} \ \),\( \ {\dot E}_{\mathrm {c}} \ \)(相順\( \ \mathrm {abc} \ \))が,抵抗\( \ R \ \)から構成される\( \ \fbox { (1) } \ \)結線された負荷と三相電流源に長距離電線により接続されている。長距離電線はインダクタンス\( \ L \ \)で表せるとする。電流源の電流は瞬時値形式で以下のように書け,高調波の発生源であることを表している(\( \ \omega T=2\pi \ \))。
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
i_{\mathrm {a}}\left( t\right) &=& \sqrt {2}I_{3}\sin 3 \omega t+\sqrt {2}I_{5}\sin 5 \omega t \\[ 5pt ]
i_{\mathrm {b}}\left( t\right) &=& \displaystyle \sqrt {2}I_{3}\sin 3 \omega \left( t-\frac {T}{3}\right) +\sqrt {2}I_{5}\sin 5 \omega \left( t-\frac {T}{3}\right) =\sqrt {2}I_{3}\sin 3 \omega t+\sqrt {2}I_{5}\sin \left( 5\omega t+\frac {2}{3}\pi \right) \\[ 5pt ]
i_{\mathrm {c}}\left( t\right) &=& \displaystyle \sqrt {2}I_{3}\sin 3 \omega \left( t+\frac {T}{3}\right) +\sqrt {2}I_{5}\sin 5 \omega \left( t+\frac {T}{3}\right) =\sqrt {2}I_{3}\sin 3 \omega t+\sqrt {2}I_{5}\sin \left( 5\omega t-\frac {2}{3}\pi \right) \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
図の回路は全て線形な要素から構成されており,重ね合わせの理が成り立つ。よって,\( \ \fbox { (2) } \ \)が全て開放され電圧源のみがある回路\( \ \mathrm {A} \ \)と,電圧源が全て\( \ \fbox { (3) } \ \)され電流源のみがある回路\( \ \mathrm {B} \ \)の状態を独立に計算した後で重ね合わせれば回路の状態を知ることができる。回路\( \ \mathrm {A} \ \)には高調波は含まれないので,以下回路\( \ \mathrm {B} \ \)のみを考える。
回路\( \ \mathrm {B} \ \)の計算では\( \ 3 \ \)次と\( \ 5 \ \)次の高調波が生じるが,次数によってインピーダンス等も異なるので次数ごとに取り扱う。\( \ 5 \ \)次の高調波電流三相分の和は\( \ \fbox { (4) } \ \)であり\( \ \fbox { (5) } \ \)には流れないため電圧源と負荷にインピーダンスに従って分流する。よって電圧源側へ戻る\( \ 5 \ \)次電流成分の大きさ(実効値)は\( \ \fbox { (6) } \ \)であり,これにより生じる高調波発生源の対地電圧の\( \ 5 \ \)次成分の大きさ(実効値)は\( \ \fbox { (7) } \ \)である。
一方,\( \ 3 \ \)次の高調波電流は中性点\( \ \mathrm {N}_{2} \ \)の接地線に流れるが,\( \ \fbox { (1) } \ \)結線である負荷側には流れない。電圧源側へ戻る\( \ 3 \ \)次電流成分の大きさ(実効値)は\( \ \fbox { (8) } \ \),電圧源の中性点から接地抵抗\( \ R_{\mathrm {g}} \ \)を経て大地へ流れる\( \ 3 \ \)次電流成分の大きさ(実効値)は\( \ \fbox { (9) } \ \)であるから高調波発生源の対地電圧の\( \ 3 \ \)次成分の大きさ(実効値)は\( \ \fbox { (10) } \ \)である。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& 負荷 &(ロ)& インダクタンス \ L &(ハ)& 中性点 \ \mathrm {N}_{2} \ の接地線 \\[ 5pt ]
&(ニ)& 短絡 &(ホ)& \Delta &(ヘ)& \mathrm {Y} \\[ 5pt ]
&(ト)& 電流源 &(チ)& 3I_{3} &(リ)& I_{3} \\[ 5pt ]
&(ヌ)& 遮断 &(ル)& 一相分の三倍 &(ヲ)& 0 \\[ 5pt ]
&(ワ)& 3I_{3}\sqrt {{R_{\mathrm {g}}}^{2}+\omega ^{2}L^{2}} &(カ)& \frac {225\omega ^{2}L^{2}I_{5}}{\sqrt {R^{2}+225\omega ^{2}L^{2}}} &(ヨ)& \frac {5\omega LRI_{5}}{\sqrt {R^{2}+225\omega ^{2}L^{2}}} \\[ 5pt ]
&(タ)& \frac {27\omega LI_{3}}{\sqrt {R^{2}+81\omega ^{2}L^{2}}} &(レ)& \frac {15\omega LI_{5}}{\sqrt {R^{2}+225\omega ^{2}L^{2}}} &(ソ)& \frac {9\omega LI_{3}}{\sqrt {R^{2}+81\omega ^{2}L^{2}}} \\[ 5pt ]
&(ツ)& \frac {RI_{5}}{\sqrt {R^{2}+225\omega ^{2}L^{2}}} &(ネ)& 27\omega LI_{3} && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
高調波発生源を含む三相回路の計算を行う問題です。
空欄が\( \ 10 \ \)個あり電流源を含む回路であるため,一見すると難しそうですが,例年の問5の問題に比べれば比較的取り組みやすく,時間的にも余裕がある問題となります。
それぞれの高調波について等価回路を描き,丁寧に解いていくことが結果的に完答への近道となります。
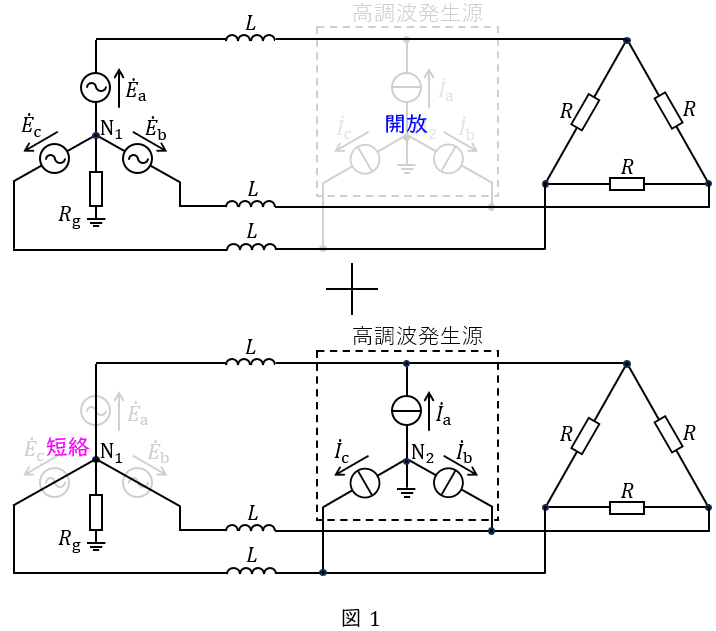
1.重ね合わせの理
複数の電源で構成された回路は,電源毎に計算した電流を重ね合わせて求めることができます。この時,電圧源は短絡,電流源は開放します。本問において回路は図1のように分解できます。
2.三角関数の加法定理
任意の角度\( \ \alpha \ \mathrm {[rad]} \ \)及び\( \ \beta \ \mathrm {[rad]} \ \)に対し,
\[
\begin{eqnarray}
\sin \left( \alpha + \beta \right) &=&\sin \alpha \cos \beta +\cos \alpha \sin \beta \\[ 5pt ]
\sin \left( \alpha – \beta \right) &=&\sin \alpha \cos \beta -\cos \alpha \sin \beta \\[ 5pt ]
\cos \left( \alpha + \beta \right) &=&\cos \alpha \cos \beta -\sin \alpha \sin \beta \\[ 5pt ]
\cos \left( \alpha – \beta \right) &=&\cos \alpha \cos \beta +\sin \alpha \sin \beta \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,これを加法定理と呼びます。
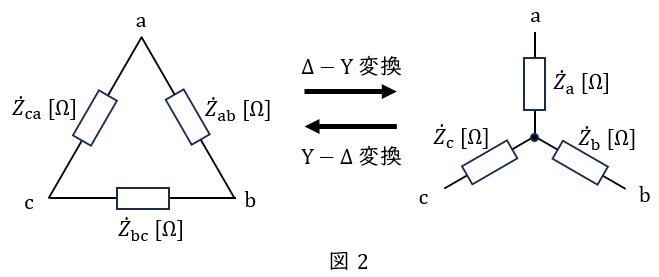
3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図2において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図2において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ホ
題意より解答候補は,(ホ)\( \ \Delta \ \),(ヘ)\( \ \mathrm {Y} \ \),になると思います。
図における抵抗\( \ R \ \)の接続方法は\( \ \Delta \ \)結線となります。
(2)解答:ト
題意より解答候補は,(イ)負荷,(ハ)中性点\( \ \mathrm {N}_{2} \ \)の接地線,(ト)電流源,になると思います。
ワンポイント解説「1.重ね合わせの理」の通り,重ね合わせの理において開放されるのは電流源となります。
(3)解答:ニ
題意より解答候補は,(ニ)短絡,(ヌ)遮断,になると思います。
ワンポイント解説「1.重ね合わせの理」の通り,電流源のみの回路を考える場合,電圧源は短絡します。
(4)解答:ヲ
与式に加法定理を適用すると,\( \ 5 \ \)次の高調波電流の三相分の和\( \ i_{5}\left( t\right) \ \)は,ワンポイント解説「2.三角関数の加法定理」の通り,
\[
\begin{eqnarray}
i_{5}\left( t\right) &=&i_{\mathrm {a5}}\left( t\right)+i_{\mathrm {b5}}\left( t\right) +i_{\mathrm {c5}}\left( t\right) \\[ 5pt ]
&=&\sqrt {2}I_{5}\sin 5 \omega t +\sqrt {2}I_{5}\sin \left( 5\omega t+\frac {2}{3}\pi \right) +\sqrt {2}I_{5}\sin \left( 5\omega t-\frac {2}{3}\pi \right) \\[ 5pt ]
&=&\sqrt {2}I_{5}\sin 5 \omega t +\sqrt {2}I_{5} \left( \sin 5 \omega t \cos \frac {2}{3}\pi +\cos 5 \omega t \sin \frac {2}{3}\pi \right) +\sqrt {2}I_{5} \left( \sin 5 \omega t \cos \frac {2}{3}\pi -\cos 5 \omega t \sin \frac {2}{3}\pi \right) \\[ 5pt ]
&=&\sqrt {2}I_{5}\sin 5 \omega t +2\sqrt {2}I_{5} \sin 5 \omega t \cos \frac {2}{3}\pi \\[ 5pt ]
&=&\sqrt {2}I_{5}\sin 5 \omega t +2\sqrt {2}I_{5} \sin 5 \omega t \times \left( -\frac {1}{2}\right) \\[ 5pt ]
&=&\sqrt {2}I_{5}\sin 5 \omega t -\sqrt {2}I_{5} \sin 5 \omega t \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ハ
題意より解答候補は,(イ)負荷,(ハ)中性点\( \ \mathrm {N}_{2} \ \)の接地線,(ト)電流源,になると思います。
(4)より,\( \ 5 \ \)次の高調波電流の三相分の和は零であるため,中性点\( \ \mathrm {N}_{2} \ \)の接地線には電流が流れないことになります。
(6)解答:ツ
負荷の抵抗\( \ R \ \)を\( \ \Delta -\mathrm {Y} \ \)変換すると,ワンポイント解説「3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り,各抵抗の大きさは\( \ \displaystyle \frac {R}{3} \ \)となるので,\( \ 5 \ \)次の高調波電流に対する一相分等価回路は図3のようになる。
よって,分流の法則を適用すると,電圧源側へ戻る\( \ 5 \ \)次電流成分の大きさ(実効値)\( \ I_{\mathrm {5r}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {5r}} &=&\frac {\displaystyle \frac {R}{3}}{\displaystyle \sqrt {\left( \frac {R}{3}\right) ^{2}+\left( 5\omega L\right) ^{2}}}I_{5} \\[ 5pt ]
&=&\frac {R}{\displaystyle 3\sqrt {\frac {R^{2}}{9} +25\omega ^{2}L^{2}}}I_{5} \\[ 5pt ]
&=&\frac {RI_{5}}{\sqrt {R^{2}+225\omega ^{2}L^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
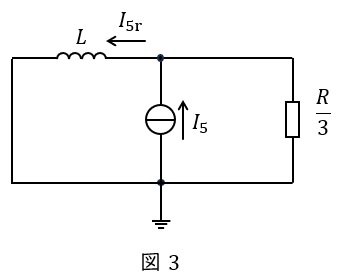
(7)解答:ヨ
図3より,高調波発生源の対地電圧の\( \ 5 \ \)次成分の大きさ(実効値)\( \ V_{5} \ \)は,リアクトルでの電圧降下と等しいから,
\[
\begin{eqnarray}
V_{\mathrm {5}} &=&5\omega LI_{\mathrm {5r}} \\[ 5pt ]
&=&5\omega L\cdot \frac {RI_{5}}{\sqrt {R^{2}+225\omega ^{2}L^{2}}} \\[ 5pt ]
&=&\frac {5\omega LRI_{5}}{\sqrt {R^{2}+225\omega ^{2}L^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(8)解答:リ
\( \ 3 \ \)次の高調波電流は負荷側に電流が流れないので,回路図は図4のようになる。
図4より,電圧源側へ戻る\( \ 3 \ \)次電流成分の大きさ(実効値)は\( \ I_{3} \ \)と求められる。
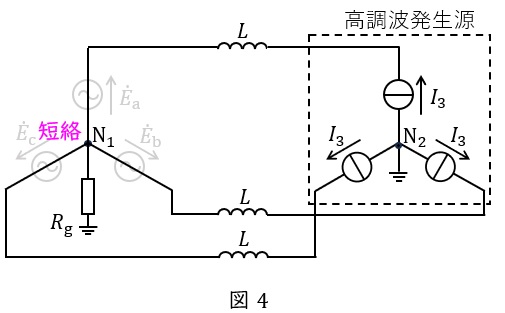
(9)解答:チ
与式より,第\( \ 3 \ \)次の高調波電流は三相とも等しいので,電圧源の中性点から接地抵抗\( \ R_{\mathrm {g}} \ \)を経て大地へ流れる\( \ 3 \ \)次電流成分の大きさ(実効値)は\( \ 3I_{3} \ \)と求められる。
(10)解答:ワ
\( \ R_{\mathrm {g}} \ \)と\( \ L \ \)に対し電圧降下を考えれば,高調波発生源の対地電圧の\( \ 3 \ \)次成分の大きさ(実効値)\( \ V_{3} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {3}} &=&\sqrt {\left( R_{\mathrm {g}}\cdot 3I_{3}\right) ^{2}+\left( 3\omega L I_{3}\right) ^{2}} \\[ 5pt ]
&=&3I_{3}\sqrt { {R_{\mathrm {g}}}^{2}+\omega ^{2}L^{2} } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん