【問題】
【難易度】★★★☆☆(普通)
次の文章は,平行平板コンデンサに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
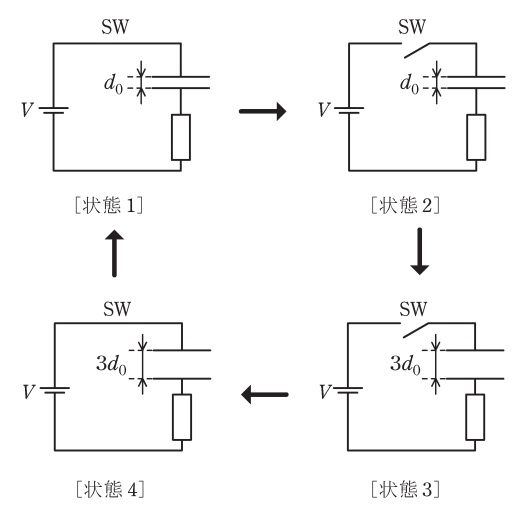
面積\( \ S \ \)で同形の導体板\( \ 2 \ \)枚からなる平行平板コンデンサが真空中に置かれている。真空の誘電率は\( \ \varepsilon _{0} \ \)である。電極間の距離\( \ d \ \)は変更することができる。最初,電極間の距離を\( \ d=d_{0} \ \)とし,図のようにコンデンサ,電圧\( \ V \ \)の電源,スイッチ\( \ \mathrm {SW} \ \),負荷抵抗が直列に接続され,\( \ \mathrm {SW} \ \)を閉じて十分な時間が経過している。これを[状態1]としたとき,コンデンサの静電容量は\( \ \fbox { (1) } \ \)で,そこで蓄えられた電荷は\( \ \fbox { (2) } \ \)である。
ここで,[状態2]のように\( \ \mathrm {SW} \ \)を開いて電源を切り離した状態とし,電極に外力を加えながら,電極間の距離をゆっくりと\( \ d=3d_{0} \ \)まで広げ,[状態3]にした。このとき,外力がコンデンサにした仕事量は\( \ \fbox { (3) } \ \)であり,それがそのままコンデンサにエネルギーとして蓄えられた。
次に,[状態4]のように\( \ \mathrm {SW} \ \)を閉じて電源に接続すると,電流が流れ,十分な時間が経過するとコンデンサの電圧が電源電圧\( \ V \ \)になる。このとき,コンデンサに蓄えられている電荷は\( \ \fbox { (4) } \ \)で,負荷抵抗で消費したエネルギーは\( \ \displaystyle \frac {2\varepsilon _{0}S}{3d_{0}}V^{2} \ \)であった。
最後に,\( \ \mathrm {SW} \ \)を閉じたまま,電極に外力を加えながら,電極間の距離をゆっくりと\( \ d=d_{0} \ \)まで狭め,[状態1]まで戻した。ただし,この操作における電流は極めて小さいため,負荷抵抗における消費電力は無視できるとみなしてよい。\( \ d=d_{0} \ \)に至るまでに電源が供給したエネルギーは\( \ \fbox { (5) } \ \)である。
[状態1]から[状態2],[状態3],[状態4]を経て再び[状態1]に戻す操作を\( \ 1 \ \)サイクルと呼ぶ。\( \ 1 \ \)サイクルで電源が供給した電荷の合計は\( \ 0 \ \)であり,電源が供給したエネルギーは\( \ \fbox { (6) } \ \)である。よって,このサイクルでは,コンデンサが,機械エネルギーを電気エネルギーに変換して負荷抵抗に供給する発電機の役割をしていることが分かる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\varepsilon _{0}S}{2d_{0}} &(ロ)& \frac {\varepsilon _{0}S}{2d_{0}}V^{2} &(ハ)& \frac {3\varepsilon _{0}S}{2d_{0}}V^{2} \\[ 5pt ]
&(ニ)& 0 &(ホ)& \frac {\varepsilon _{0}S}{d_{0}}V^{2} &(ヘ)& \frac {\varepsilon _{0}S}{6d_{0}}V^{2} \\[ 5pt ]
&(ト)& \frac {\varepsilon _{0}S}{3d_{0}}V &(チ)& \frac {\varepsilon _{0}S}{d_{0}}V &(リ)& \frac {\varepsilon _{0}S}{6d_{0}}V \\[ 5pt ]
&(ヌ)& \frac {\varepsilon _{0}S}{d_{0}} &(ル)& \frac {2\varepsilon _{0}S}{3d_{0}}V &(ヲ)& \frac {2\varepsilon _{0}S}{d_{0}}V\\[ 5pt ]
&(ワ)& \frac {4\varepsilon _{0}S}{3d_{0}}V^{2} &(カ)& \frac {2\varepsilon _{0}S}{d_{0}} &(ヨ)& \frac {\varepsilon _{0}S}{2d_{0}}V \\[ 5pt ]
&(タ)& \frac {2\varepsilon _{0}S}{3d_{0}}V^{2} &(レ)& \frac {\varepsilon _{0}S}{3d_{0}}V^{2} && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
扱う公式は少ないですが,公式を暗記しているだけでは解けない問題で,なぜそうなるのかを理解している必要がある問題です。この問題を学習することで,コンデンサの仕事に関する意味が定量的に理解できると思います。
1.コンデンサの静電容量\( \ C \ \)
コンデンサの極板面積が\( \ S \ \),極板間の距離が\( \ d \ \),誘電率が\( \ \varepsilon \ \)である時,コンデンサの静電容量\( \ C \ \)は,
\[
\begin{eqnarray}
C &=& \frac {\varepsilon S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.コンデンサの静電エネルギー\( \ W \ \)
静電容量が\( \ C \ \)のコンデンサに電圧\( \ V \ \)をかけ,十分な時間が経過した時のコンデンサの静電エネルギー\( \ W \ \)は,
\[
\begin{eqnarray}
W &=& \frac {1}{2}CV^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,蓄えられる電荷\( \ Q=CV \ \)の関係を用いると,
\[
\begin{eqnarray}
W &=& \frac {1}{2}QV \\[ 5pt ]
&=& \frac {Q^{2}}{2C} \\[ 5pt ]
\end{eqnarray}
\]
と変形できます。与えられる値に合わせ,式を変形します。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ヌ
ワンポイント解説「1.コンデンサの静電容量\( \ C \ \)」より,コンデンサの極板面積が\( \ S \ \),極板間の距離が\( \ d_{0} \ \),真空の誘電率が\( \ \varepsilon _{0} \ \)であるから,[状態1]の時の静電容量\( \ C_{1} \ \)は,
\[
\begin{eqnarray}
C_{1} &=& \frac {\varepsilon _{0} S}{d_{0}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:チ
蓄えられる電荷\( \ Q=CV \ \)の関係から,[状態1]の時に蓄えられた電荷\( \ Q_{1} \ \)は,
\[
\begin{eqnarray}
Q_{1} &=& C_{1}V \\[ 5pt ]
&=& \frac {\varepsilon _{0} S}{d_{0}}V \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
[状態2]の時の静電エネルギー\( \ W_{2} \ \)は,ワンポイント解説「2.コンデンサの静電エネルギー\( \ W \ \)」より,
\[
\begin{eqnarray}
W_{2} &=& \frac {1}{2}C_{1}V^{2} \\[ 5pt ]
&=& \frac {\varepsilon _{0} S}{2d_{0}}V^{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。[状態3]の時の静電容量\( \ C_{3} \ \)は,
\[
\begin{eqnarray}
C_{3} &=& \frac {\varepsilon _{0} S}{3d_{0}} \\[ 5pt ]
\end{eqnarray}
\]
であり,[状態2]から[状態3]に至るまで,\( \ \mathrm {SW} \ \)を開いているので,蓄えられた電荷量は変わらない。したがって,[状態3]の時の静電エネルギー\( \ W_{3} \ \)は,
\[
\begin{eqnarray}
W_{3} &=& \frac {Q_{1}^{2}}{2C_{3}} \\[ 5pt ]
&=& \frac {\displaystyle \left( \frac {\varepsilon _{0} S}{d_{0}}V\right) ^{2}}{\displaystyle 2\frac {\varepsilon _{0} S}{3d_{0}}} \\[ 5pt ]
&=& \frac {3\varepsilon _{0} S}{2d_{0}}V^{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,外力がした仕事量\( \ \Delta W \ \)は,コンデンサに蓄えられたエネルギーと等しいので,
\[
\begin{eqnarray}
\Delta W &=& W_{3}-W_{2} \\[ 5pt ]
&=& \frac {3\varepsilon _{0} S}{2d_{0}}V^{2}-\frac {\varepsilon _{0} S}{2d_{0}}V^{2} \\[ 5pt ]
&=& \frac {\varepsilon _{0} S}{d_{0}}V^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ト
蓄えられる電荷\( \ Q=CV \ \)の関係から,[状態4]の時に蓄えられた電荷\( \ Q_{4} \ \)は,
\[
\begin{eqnarray}
Q_{4} &=& C_{3}V \\[ 5pt ]
&=& \frac {\varepsilon _{0} S}{3d_{0}} V \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:タ
[状態4]から[状態1]へ変化した時の電源が供給したエネルギー\( \ \Delta W^{\prime } \ \)は,[状態4]から[状態1]へ変化した時にコンデンサに蓄えられた電荷の増加量\( \ \Delta Q \ \)に電源電圧\( \ V \ \)を掛けたものに等しい。よって,
\[
\begin{eqnarray}
\Delta W^{\prime } &=& \Delta Q V \\[ 5pt ]
&=& \left( Q_{1}-Q_{4}\right) V \\[ 5pt ]
&=& \left( \frac {\varepsilon _{0} S}{d_{0}}V-\frac {\varepsilon _{0} S}{3d_{0}}V\right) V \\[ 5pt ]
&=& \frac {2\varepsilon _{0}S}{3d_{0}}V^{2}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)解答:ニ
電源が供給したエネルギーは電源が繋がっている[状態3]から[状態4]と[状態4]から[状態1]の合計である。
[状態3]から[状態4]になる時にコンデンサに蓄えられる電荷量は\( \ Q_{1} \ \)から\( \ Q_{4} \ \)に減少し,この時のエネルギー\( \ \Delta W^{\prime \prime } \ \)は,
\[
\begin{eqnarray}
\Delta W^{\prime \prime } &=& \Delta Q V \\[ 5pt ]
&=& \left( Q_{4}-Q_{1}\right) V \\[ 5pt ]
&=& \left( \frac {\varepsilon _{0} S}{3d_{0}}V-\frac {\varepsilon _{0} S}{d_{0}}V\right) V \\[ 5pt ]
&=& -\frac {2\varepsilon _{0}S}{3d_{0}}V^{2}\\[ 5pt ]
\end{eqnarray}
\]
となり,これが抵抗で消費されたエネルギーとなった。
また,(5)より,[状態4]から[状態1]へ変化した時の電源が供給したエネルギー\( \ \Delta W^{\prime } \ \)は\( \ \displaystyle \frac {2\varepsilon _{0}S}{3d_{0}}V^{2} \ \)であった。
よって,[状態3]から[状態4]と[状態4]から[状態1]での電源が供給したエネルギーの合計は\( \ 0 \ \)となり,コンデンサでした機械的仕事が抵抗で消費される電気エネルギーとなった。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん