Contents
【問題】
【難易度】★☆☆☆☆(易しい)
次の文章は,直流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
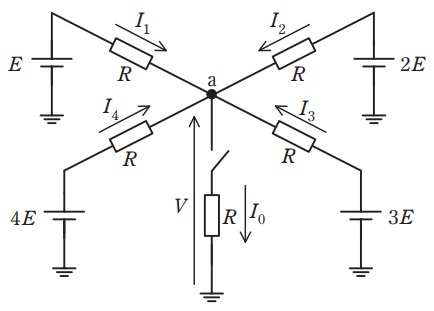
図のような\( \ 5 \ \)個の抵抗\( \ R \ \)と\( \ 4 \ \)種類の直流電圧源,スイッチからなる回路を考える。節点\( \ \mathrm {a} \ \)の電位を\( \ V \ \)とする。
(a) スイッチが開いているとき,各抵抗\( \ R \ \)の電流は\( \ I_{1}+I_{2}+I_{3}+I_{4}=0 \ \)を満たす。それぞれの抵抗\( \ R \ \)の電流を\( \ E \ \)と\( \ V \ \)と\( \ R \ \)の式で表すと,\( \ V = \ \fbox { (1) } \ \)を得る。これより各電流の比は\( \ \displaystyle \frac {I_{4}}{I_{1}}= \frac {I_{3}}{I_{2}}= \ \fbox { (2) } \ \)となる。
(b) スイッチを閉じているとき,各抵抗\( \ R \ \)の電流は\( \ I_{1}+I_{2}+I_{3}+I_{4}=I_{0} \ \)を満たす。\( \ \displaystyle I_{0}=\frac {V}{R} \ \)を利用すると\( \ V = \ \fbox { (3) } \ \)となり,各抵抗\( \ R \ \)の電流のうち,電流\( \ \fbox { (4) } \ \)は零となる。回路の消費電力は \( \ \fbox { (5) } \ \)となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 3E &(ロ)& I_{1} &(ハ)& \frac {5}{2}E \\[ 5pt ]
&(ニ)& I_{4} &(ホ)& 2E &(ヘ)& \frac {4}{R}E^{2} \\[ 5pt ]
&(ト)& -3 &(チ)& \frac {7}{2}E &(リ)& -1 \\[ 5pt ]
&(ヌ)& -2 &(ル)& \frac {6}{R}E^{2} &(ヲ)& \frac {10}{R}E^{2} \\[ 5pt ]
&(ワ)& I_{2} &(カ)& I_{3} &(ヨ)& 4E \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
直流電圧源を4つ用いた回路に関する問題です。
回路図が鳥瞰図を使用しているため一瞬驚いてしまうかもしれませんが,特にキルヒホッフの法則を適用すれば解ける問題となります。
解説では計算量が少し楽になるミルマンの定理を使用して解説しますが,解答が合っていれば必ずしも使用する必要はありません。
1.ミルマンの定理
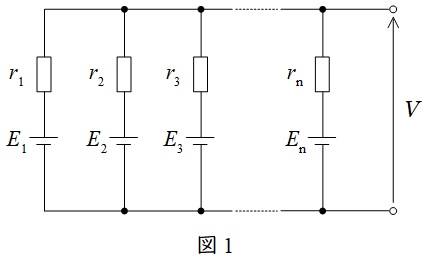
図1のような,電源\( \ E_{1},E_{2},\cdots ,E_{\mathrm {n}} \ \)と抵抗\( \ r_{1},r_{2},\cdots ,r_{\mathrm {n}} \ \)が直並列された回路における全体の電圧\( \ V \ \)は,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E_{1}}{r_{1}}+\frac {E_{2}}{r_{2}}+\frac {E_{3}}{r_{3}}+\cdots +\frac {E_{\mathrm {n}}}{r_{\mathrm {n}}}}{\displaystyle \frac {1}{r_{1}}+\frac {1}{r_{2}}+\frac {1}{r_{3}}+\cdots +\frac {1}{r_{\mathrm {n}}}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:ハ
\( \ I_{0}=0 \ \)なので\( \ I_{0} \ \)の部分の回路を無視すると,電圧\( \ V \ \)は,ワンポイント解説「1.ミルマンの定理」より,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E}{R}+\frac {2E}{R}+\frac {3E}{R}+\frac {4E}{R}}{\displaystyle \frac {1}{R}+\frac {1}{R}+\frac {1}{R}+\frac {1}{R}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {10E}{R}}{\displaystyle \frac {4}{R}} \\[ 5pt ]
&=&\frac {10E}{4} \\[ 5pt ]
&=&\frac {5}{2}E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:リ
(1)より,
\[
\begin{eqnarray}
I_{1}&=&\frac {E-V}{R} \\[ 5pt ]
&=&\frac {\displaystyle E-\frac {5}{2}E}{R} \\[ 5pt ]
&=&-\frac {3}{2}\frac {E}{R} \\[ 5pt ]
I_{2}&=&\frac {2E-V}{R} \\[ 5pt ]
&=&\frac {\displaystyle 2E-\frac {5}{2}E}{R} \\[ 5pt ]
&=&-\frac {1}{2}\frac {E}{R} \\[ 5pt ]
I_{3}&=&\frac {3E-V}{R} \\[ 5pt ]
&=&\frac {\displaystyle 3E-\frac {5}{2}E}{R} \\[ 5pt ]
&=&\frac {1}{2}\frac {E}{R} \\[ 5pt ]
I_{4}&=&\frac {4E-V}{R} \\[ 5pt ]
&=&\frac {\displaystyle 4E-\frac {5}{2}E}{R} \\[ 5pt ]
&=&\frac {3}{2}\frac {E}{R} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
\frac {I_{4}}{I_{1}}&=&\frac {\displaystyle \frac {3}{2}\frac {E}{R}}{\displaystyle -\frac {3}{2}\frac {E}{R}} \\[ 5pt ]
&=&-1 \\[ 5pt ]
\frac {I_{3}}{I_{2}}&=&\frac {\displaystyle \frac {1}{2}\frac {E}{R}}{\displaystyle -\frac {1}{2}\frac {E}{R}} \\[ 5pt ]
&=&-1 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
ワンポイント解説「1.ミルマンの定理」より,電圧\( \ V \ \)は,
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {E}{R}+\frac {2E}{R}+\frac {3E}{R}+\frac {4E}{R}+\frac {0}{R}}{\displaystyle \frac {1}{R}+\frac {1}{R}+\frac {1}{R}+\frac {1}{R}+\frac {1}{R}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {10E}{R}}{\displaystyle \frac {5}{R}} \\[ 5pt ]
&=&\frac {10E}{5} \\[ 5pt ]
&=&2E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ワ
\( \ V=2E \ \)なので,\( \ I_{2} \ \)は電位差がないため零となる。
(5)解答:ヲ
\[
\begin{eqnarray}
I_{1}&=&\frac {E-V}{R} \\[ 5pt ]
&=&\frac {\displaystyle E-2E}{R} \\[ 5pt ]
&=&-\frac {E}{R} \\[ 5pt ]
I_{2}&=&0 \\[ 5pt ]
I_{3}&=&\frac {3E-V}{R} \\[ 5pt ]
&=&\frac {\displaystyle 3E-2E}{R} \\[ 5pt ]
&=&\frac {E}{R} \\[ 5pt ]
I_{4}&=&\frac {4E-V}{R} \\[ 5pt ]
&=&\frac {\displaystyle 4E-2E}{R} \\[ 5pt ]
&=&\frac {2E}{R} \\[ 5pt ]
I_{0}&=&\frac {V}{R} \\[ 5pt ]
&=&\frac {2E}{R} \\[ 5pt ]
\end{eqnarray}
\]
であるから,回路の消費電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&R\left| I_{1}\right| ^{2}+R\left| I_{3}\right| ^{2}+R\left| I_{4}\right| ^{2}+R\left| I_{0}\right| ^{2} \\[ 5pt ]
&=&R\left( \left| I_{1}\right| ^{2}+\left| I_{3}\right| ^{2}+\left| I_{4}\right| ^{2}+\left| I_{0}\right| ^{2}\right) \\[ 5pt ]
&=&R\left\{ \left(\frac {E}{R} \right) ^{2}+\left(\frac {E}{R} \right) ^{2}+\left(\frac {2E}{R} \right) ^{2}+\left(\frac {2E}{R} \right) ^{2}\right\} \\[ 5pt ]
&=&R\cdot \frac {E^{2}+E^{2}+4E^{2}+4E^{2}}{R^{2}} \\[ 5pt ]
&=&\frac {10}{R}E^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは