Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,半導体のキャリヤが非熱平衡状態から熱平衡状態に戻るときの過渡状態に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は語句を解答群の中から選び,その記号をマークシートに記入しなさい。
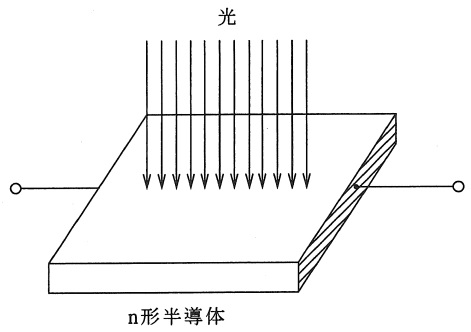
図のように,熱平衡状態にある\( \ \mathrm {n} \ \)形半導体に光を照射して,一様に過剰キャリヤを生成させた後,光の照射を止めた場合の過剰キャリヤの減衰過程を考察する。熱平衡状態にあるときの\( \ \mathrm {n} \ \)形半導体の電子密度を\( \ n_{\mathrm {0}} \ \),正孔密度を\( \ p_{\mathrm {0}} \ \)とする。光照射による外部エネルギーを得て,生成された過剰キャリヤの過剰電子密度を\( \ \mathit {\Delta } n \ \),過剰正孔密度を\( \ \mathit {\Delta } p \ \)とする。これら過剰キャリヤは対生成であるので,\( \ \mathit {\Delta } n \ \)と\( \ \mathit {\Delta } p \ \)の量的関係は\( \ \fbox { (1) } \ \)である。光照射を止めた直後では,電子密度\( \ n \ \)と正孔密度\( \ p \ \)は\( \ n=n_{\mathrm {0}}+\mathit {\Delta } n \ \)及び\( \ p=p_{\mathrm {0}}+\mathit {\Delta } p \ \)である。なお,ここではキャリヤの生成量が少なく,\( \ \mathit {\Delta } n ≪n_{\mathrm {0}} \ \),\( \ \mathit {\Delta } p ≪n_{\mathrm {0}} \ \)である場合を考える。
二つのエネルギー準位間において,単位体積当たり高いエネルギー準位へ単位時間に遷移する電子の数を\( \ R_{up} \ \),低いエネルギー準位へ単位時間に遷移する電子の数を\( \ R_{down} \ \)とすると,\( \ R_{up}=K_{up}n_{\mathrm {0}}p_{\mathrm {0}} \ \)及び\( \ R_{down}=K_{down}\left( n_{\mathrm {0}}+\mathit {\Delta } n\right) \left( p_{\mathrm {0}}+\mathit {\Delta } p\right) \ \)(ただし,\( \ K_{up} \ \)及び\( \ K_{down} \ \)は比例定数)と書ける。この場合,\( \ \mathit {\Delta } n ≪n_{\mathrm {0}} \ \),\( \ \mathit {\Delta } p ≪n_{\mathrm {0}} \ \)であるので,光照射を止めた後も熱平衡状態に近いとして,\( \ K=K_{up}=K_{down} \ \)とする。このとき,単位体積当たり単位時間に再結合する正味の電子の数\( \ R \ \)は\( \ R_{down}-R_{up} \ \)であり,\( \ \mathit {\Delta } n ≪n_{\mathrm {0}} \ \),\( \ \mathit {\Delta } p ≪n_{\mathrm {0}} \ \)及び\( \ \mathrm {n} \ \)形半導体\( \ \left( n_{\mathrm {0}}≫p_{\mathrm {0}}\right) \ \)であることに注意すれば,
\[
\begin{eqnarray}
R &=& \ \fbox { (2) } \ ・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
と近似される。このことから\( \ \mathit {\Delta } p \ \)の減少する時間的変化を表す等式は
\[
\begin{eqnarray}
&& \ \fbox { (3) } \ ・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
と書ける。時刻\( \ t=0 \ \)における過剰正孔密度を\( \ \mathit {\Delta } p \left( 0 \right) \ \)とするとき②式を解けば
\[
\begin{eqnarray}
\mathit {\Delta } p &=& \ \fbox { (4) } \ ・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \displaystyle \tau _{p}=\frac {1}{Kn_{0}} \ \)としたとき,\( \ \tau _{p} \ \)を正孔の\( \ \fbox { (5) } \ \)という。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& -\frac {\mathrm {d}\mathit {\Delta }p}{\mathrm {d}t}=K\mathit {\Delta }p &(ロ)& \mathit {\Delta }n=\mathit {\Delta }p &(ハ)& \mathit {\Delta }n>\mathit {\Delta }p \\[ 5pt ]
&(ニ)& \mathit {\Delta }p \left( 0 \right) \mathrm {e}^{Kn_{0}t} &(ホ)& 周 期 &(ヘ)& -\frac {\mathrm {d}\mathit {\Delta }p}{\mathrm {d}t}=Kn_{0}\mathit {\Delta }p \\[ 5pt ]
&(ト)& \mathit {\Delta }n<\mathit {\Delta }p &(チ)& 寿 命 &(リ)& 結合速度 \\[ 5pt ]
&(ヌ)& Kn_{0}\mathit {\Delta }p &(ル)& \frac {\mathrm {d}\mathit {\Delta }p}{\mathrm {d}t}=Kn_{0}\mathit {\Delta }p &(ヲ)& \left( p_{0}+\mathit {\Delta }p\right) +\mathit {\Delta }p \left( 0 \right) \mathrm {e}^{-Kn_{0}t} \\[ 5pt ]
&(ワ)& K\mathit {\Delta }n\mathit {\Delta }p &(カ)& K\mathit {\Delta }p &(ヨ)& \mathit {\Delta }p \left( 0 \right) \mathrm {e}^{-Kn_{0}t} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
半導体中の電子の再結合に関する問題です。
電験のテキストにはあまり記載されておらず,文章を読みながら近似や微分方程式を使って解いていく問題で,高い文章理解力が求められる問題です。
問8の方が比較的取り組みやすい問題でしたので,多くの受験生は本問を選択しなかったと予想されます。
1.\( \ \mathrm {n} \ \)形半導体のエネルギー帯
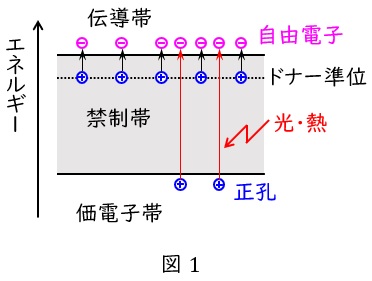
\( \ \mathrm {n} \ \)形半導体は真性半導体に\( \ 5 \ \)価のリン\( \ \mathrm {P} \ \)やヒ素\( \ \mathrm {As} \ \)等(ドナー)を混ぜる(ドープする)ことで,真性半導体よりも電気が流れやすくなったもので,エネルギー帯は図1のようになります。
価電子により占有されているエネルギー帯を価電子帯,電子が取りうることができないエネルギー帯を禁制帯,自由電子が取りうるエネルギー帯を伝導帯といい,ドナーは伝導帯付近にドナー準位を形成することで容易に自由電子になります。また,光や熱等のエネルギーを加えることで励起され,新たに電子-正孔対ができるので,全体としては図1のような多数キャリヤの自由電子と少数キャリヤの正孔ができることになります。
【解答】
(1)解答:ロ
ワンポイント解説「1.\( \ \mathrm {n} \ \)形半導体のエネルギー帯」の通り,過剰キャリヤは電子-正孔の対生成となるので,\( \ \mathit {\Delta }n=\mathit {\Delta }p \ \)と求められる。
(2)解答:ヌ
問題文に沿って式を立てると,
\[
\begin{eqnarray}
R &=& R_{down}-R_{up} \\[ 5pt ]
&=& K_{down}\left( n_{\mathrm {0}}+\mathit {\Delta } n\right) \left( p_{\mathrm {0}}+\mathit {\Delta } p\right)-K_{up}n_{\mathrm {0}}p_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ K=K_{up}=K_{down} \ \)であるから,
\[
\begin{eqnarray}
R &=& K\left( n_{\mathrm {0}}+\mathit {\Delta } n\right) \left( p_{\mathrm {0}}+\mathit {\Delta } p\right)-Kn_{\mathrm {0}}p_{\mathrm {0}} \\[ 5pt ]
&=& K\left\{ \left( n_{\mathrm {0}}+\mathit {\Delta } n\right) \left( p_{\mathrm {0}}+\mathit {\Delta } p\right)-n_{\mathrm {0}}p_{\mathrm {0}}\right\} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \mathit {\Delta } n ≪n_{\mathrm {0}} \ \)より,
\[
\begin{eqnarray}
R &≃& K\left\{ n_{\mathrm {0}} \left( p_{\mathrm {0}}+\mathit {\Delta } p\right)-n_{\mathrm {0}}p_{\mathrm {0}}\right\} \\[ 5pt ]
&=& K\left( n_{\mathrm {0}}p_{\mathrm {0}}+n_{\mathrm {0}}\mathit {\Delta } p-n_{\mathrm {0}}p_{\mathrm {0}}\right) \\[ 5pt ]
&=& Kn_{\mathrm {0}}\mathit {\Delta } p \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヘ
(2)解答式より,\( \ \mathit {\Delta } p \ \)の減少する時間的変化\( \ \displaystyle -\frac {\mathrm {d}\mathit {\Delta }p}{\mathrm {d}t} \ \)は,
\[
\begin{eqnarray}
-\frac {\mathrm {d}\mathit {\Delta }p}{\mathrm {d}t}&=& R \\[ 5pt ]
&=& Kn_{\mathrm {0}}\mathit {\Delta } p \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
(3)解答式を変数分離して解くと,
\[
\begin{eqnarray}
-\frac {\mathrm {d}\mathit {\Delta }p}{\mathrm {d}t}&=& Kn_{\mathrm {0}}\mathit {\Delta } p \\[ 5pt ]
\frac {1}{\mathit {\Delta } p}\mathrm {d}\mathit {\Delta }p&=&-Kn_{\mathrm {0}}\mathrm {d}t \\[ 5pt ]
\int \frac {1}{\mathit {\Delta } p}\mathrm {d}\mathit {\Delta }p&=&\int -Kn_{\mathrm {0}}\mathrm {d}t \\[ 5pt ]
\ln \mathit {\Delta }p&=&-Kn_{\mathrm {0}}t+C \left( C \ は積分定数\right) \\[ 5pt ]
\mathit {\Delta }p&=&A\mathrm {e}^{-Kn_{\mathrm {0}}t} \left( A=\mathrm {e}^{C} \right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,「時刻\( \ t=0 \ \)における過剰正孔密度を\( \ \mathit {\Delta } p \left( 0 \right) \ \)とする」となっていることから,
\[
\begin{eqnarray}
\mathit {\Delta } p \left( 0 \right) &=&A\mathrm {e}^{-Kn_{\mathrm {0}}\times 0} \\[ 5pt ]
A&=&\mathit {\Delta } p \left( 0 \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\mathit {\Delta }p&=&\mathit {\Delta } p \left( 0 \right) \mathrm {e}^{-Kn_{\mathrm {0}}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:チ
\( \ \displaystyle \tau _{p}=\frac {1}{Kn_{0}} \ \)とすると,これは(4)解答式において\( \ 63.2 \ \mathrm {[%]} \ \)変化した時間(時定数)であり,正孔の寿命と呼ばれる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは