Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相リアクトルに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
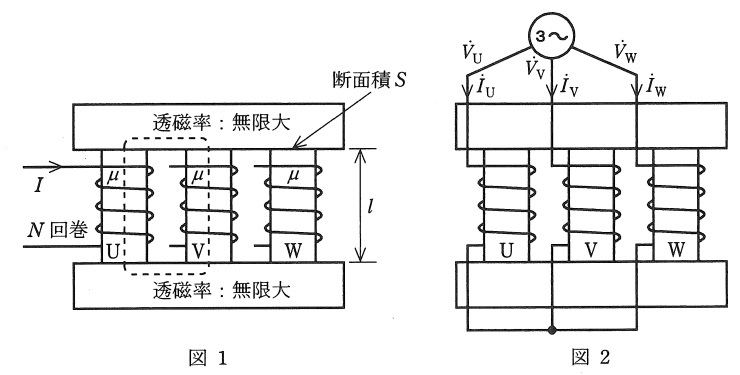
図1のように,継鉄(横方向)部分の透磁率が無限大,脚(縦方向)部分の透磁率が\( \ \mu \ \),長さが\( \ l \ \),断面積が\( \ S \ \)である三相変圧器用三脚鉄心に,\( \ \mathrm {U} \ \),\( \ \mathrm {V} \ \),\( \ \mathrm {W} \ \)の三相巻線が施されている。巻数はすべて\( \ N \ \)回である。\( \ \mathrm {U} \ \)相巻線のみに電流\( \ I \ \)を流したとき,\( \ \mathrm {U} \ \),\( \ \mathrm {V} \ \),\( \ \mathrm {W} \ \)相鉄心に生じる磁界の強さをそれぞれ\( \ H_{1} \ \),\( \ H_{2} \ \),\( \ H_{3} \ \)とする。継鉄部分の磁界の強さは\( \ \fbox { (1) } \ \)と見なせる。\( \ \mathrm {U} \ \)相巻線と鎖交する磁束は\( \ 2 \ \)分され,それぞれが\( \ \mathrm {V} \ \),\( \ \mathrm {W} \ \)相巻線と逆方向に鎖交して戻ると考えられるので,\( \ H_{2} = H_{3} \ \)である。したがって,図1の破線で示した積分路について,アンペールの周回積分の法則を適用すると,
\[
\begin{eqnarray}
&& \ \fbox { (2) } \ ・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
が与えられる。\( \ \mathrm {U} \ \)相鉄心に生じる磁束密度を\( \ B_{1} \ \),\( \ \mathrm {V} \ \),\( \ \mathrm {W} \ \)相鉄心に生じる磁束密度を\( \ B_{2} \ \)とすると,
\[
\begin{eqnarray}
B_{1}&=& \mu H_{1} \\[ 5pt ]
B_{2}&=& \mu H_{2} \\[ 5pt ]
B_{1}&=&2B_{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係が成り立つ。これらの関係から①式を\( \ B_{1} \ \)について解くと,
\[
\begin{eqnarray}
B_{1}&=& \ \fbox { (3) } \\[ 5pt ]
\end{eqnarray}
\]
が得られる。\( \ \mathrm {U} \ \)相鉄心の磁束は\( \ \phi _{1}=B_{1}S \ \),\( \ \mathrm {U} \ \)相巻線との総鎖交磁束は\( \ \mathit {\Phi }_{1}=N\phi _{1} \ \)であるから,この巻線の自己インダクタンス\( \ L \ \)は
\[
\begin{eqnarray}
L&=& \ \fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
である。
また,同様に\( \ 2 \ \)巻線間の相互インダクタンス\( \ M \ \)は
\[
\begin{eqnarray}
M&=&\frac {1}{2}L ・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
である。
図2のように,このリアクトルを\( \ \mathrm {Y} \ \)結線とし,対称三相交流電源に接続した場合,各相の電圧をそれぞれ\( \ {\dot V}_{\mathrm {U}} \ \),\( \ {\dot V}_{\mathrm {V}} \ \),\( \ {\dot V}_{\mathrm {W}} \ \),各相の電流をそれぞれ\( \ {\dot I}_{\mathrm {U}} \ \),\( \ {\dot I}_{\mathrm {V}} \ \),\( \ {\dot I}_{\mathrm {W}} \ \)とすると,
\[
\begin{eqnarray}
\begin{bmatrix}
{\dot V}_{\mathrm {U}} \\
{\dot V}_{\mathrm {V}} \\
{\dot V}_{\mathrm {W}}
\end{bmatrix}
&=&\mathrm {j}\omega
\begin{bmatrix}
L & M & M \\
M & L & M \\
M & M & L
\end{bmatrix}
\begin{bmatrix}
{\dot I}_{\mathrm {U}} \\
{\dot I}_{\mathrm {V}} \\
{\dot I}_{\mathrm {W}}
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
の関係が成り立つ。ただし,巻線の抵抗は無視できるものとする。\( \ {\dot V}_{\mathrm {U}} \ \)についての関係式は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {U}}&=&\mathrm {j}\omega \left( L{\dot I}_{\mathrm {U}}+M{\dot I}_{\mathrm {V}}+M{\dot I}_{\mathrm {W}}\right) \\[ 5pt ]
\end{eqnarray}
\]
であり,②式より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {U}}&=&\mathrm {j}\omega L\left( {\dot I}_{\mathrm {U}}+\frac {1}{2}{\dot I}_{\mathrm {V}}+\frac {1}{2}{\dot I}_{\mathrm {W}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と変形できる。相間の位相差が\( \ \displaystyle \frac {2\pi }{3} \ \)であることに注意してベクトル合成すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {U}}&=& \ \fbox { (5) } \ \mathrm {j}\omega L{\dot I}_{\mathrm {U}} \\[ 5pt ]
\end{eqnarray}
\]
となる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& H_{1}l+H_{2}l=N^{2}I &(ロ)& \frac {3\mu NI}{2l} &(ハ)& \frac {2\mu NS}{3l} \\[ 5pt ]
&(ニ)& H_{1} &(ホ)& \frac {2\mu N^{2}S}{3l} &(ヘ)& \infty \\[ 5pt ]
&(ト)& \frac {1}{\sqrt{3}} &(チ)& H_{1}l+H_{2}l=NI &(リ)& \frac {\mu N^{2}S}{l} \\[ 5pt ]
&(ヌ)& \frac {2\mu NI}{3l} &(ル)& \frac {1}{\sqrt{2}} &(ヲ)& 0 \\[ 5pt ]
&(ワ)& \frac {\mu NI}{l} &(カ)& \frac {1}{2} &(ヨ)& H_{1}l=NI \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相リアクトルに関する問題で,問題文が長く受験生を混乱させるような内容となっていますが,しっかりと基本公式を理解していれば解ける問題です。
試験本番でも見た目に騙されない様,あまり焦らず落ち着いて解くようにしましょう。
1.アンペールの周回積分の法則
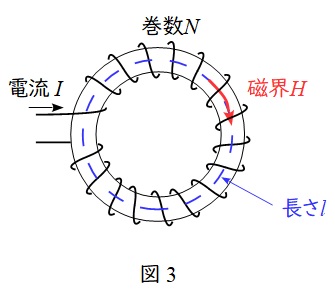
図3の示すような,電流\( \ I \ \)が流れている環状ソレノイドの中心に発生する磁界の大きさ\( \ H \ \)には,アンペールの周回積分の法則が適用され,
\[
\begin{eqnarray}
NI&=&\int H \mathrm {d}l \\[ 5pt ]
\end{eqnarray}
\]
が成立します。ソレノイド中心部の磁界が等しいとすれば,
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係
透磁率が\( \ \mu \ \)の時,磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係は,
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)
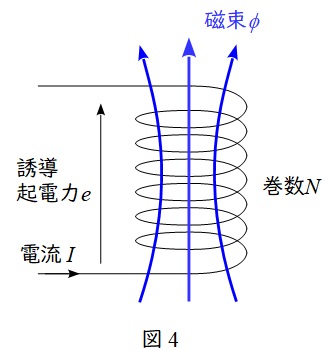
図4において,巻数\( \ N \ \)のコイルを貫通する磁束\( \ \phi \ \)があるとき,ファラデーの電磁誘導の法則より,コイルに発生する誘導起電力\( \ e \ \)は,磁束の時間変化に比例し,
\[
\begin{eqnarray}
e&=&−N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。これをファラデーの電磁誘導の法則といいます。このとき,電流変化によりコイル内の磁束が変化したと考えれば,
\[
\begin{eqnarray}
e&=&−L\frac {\mathrm {d}I }{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
という関係も成り立ち,\( \ L \ \)を自己インダクタンスと言います。これらの関係から,
\[
\begin{eqnarray}
−N\frac {\mathrm {d}\phi }{\mathrm {d}t}&=&−L\frac {\mathrm {d}I }{\mathrm {d}t} \\[ 5pt ]
N\phi &=&LI \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(1)解答:ヲ
ワンポイント解説「2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係」より,透磁率が\( \ \mu \ \)の時,磁界の大きさ\( \ H \ \)は,
\[
\begin{eqnarray}
H&=&\frac {B}{\mu } \\[ 5pt ]
\end{eqnarray}
\]
であり,継鉄部分の透磁率\( \ \mu \ \)が無限大であることから,
\[
\begin{eqnarray}
H&≒&0 \\[ 5pt ]
\end{eqnarray}
\]
となることがわかる。
(2)解答:チ
アンペールの周回積分の法則を図1に適用すると,
\[
\begin{eqnarray}
NI&=&\int H \mathrm {d}l \\[ 5pt ]
&=& H_{1}l+H_{2}l \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヌ
(2)の解答式に,\( \ \displaystyle H_{1}=\frac {B_{1}}{\mu } \ \),\( \ \displaystyle H_{2}=\frac {B_{2}}{\mu }=\frac {B_{1}}{2\mu } \ \)を代入して整理すると,
\[
\begin{eqnarray}
NI&=& \frac {B_{1}}{\mu }\cdot l+\frac {B_{1}}{2\mu }\cdot l \\[ 5pt ]
&=& \frac {3B_{1}l}{2\mu } \\[ 5pt ]
B_{1}&=& \frac {2\mu NI}{3l} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ホ
題意より,\( \ \mathrm {U} \ \)相巻線との総鎖交磁束は,
\[
\begin{eqnarray}
\mathit {\Phi }_{1}&=&N\phi _{1} \\[ 5pt ]
&=&NB_{1}S \\[ 5pt ]
&=& \frac {2\mu N^{2}IS}{3l}\\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「3.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)」の通り,自己インダクタンス\( \ L \ \)は,
\[
\begin{eqnarray}
LI&=&N\phi _{1} \\[ 5pt ]
&=&\frac {2\mu N^{2}IS}{3l} \\[ 5pt ]
L&=& \frac {2\mu N^{2}S}{3l}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
\( \ \mathrm {U} \ \)相電圧\( \ {\dot V}_{\mathrm {U}} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {U}}&=&\mathrm {j}\omega L\left( {\dot I}_{\mathrm {U}}+\frac {1}{2}{\dot I}_{\mathrm {V}}+\frac {1}{2}{\dot I}_{\mathrm {W}}\right) \\[ 5pt ]
&=&\frac {1}{2}\mathrm {j}\omega L\left( 2{\dot I}_{\mathrm {U}}+{\dot I}_{\mathrm {V}}+{\dot I}_{\mathrm {W}}\right) \\[ 5pt ]
&=&\frac {1}{2}\mathrm {j}\omega L\left\{ {\dot I}_{\mathrm {U}}+\left( {\dot I}_{\mathrm {U}}+{\dot I}_{\mathrm {V}}+{\dot I}_{\mathrm {W}}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
と整理され,対称三相交流電源においては,\( \ {\dot I}_{\mathrm {U}}+{\dot I}_{\mathrm {V}}+{\dot I}_{\mathrm {W}}=0 \ \)であるから,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {U}}&=&\frac {1}{2}\mathrm {j}\omega L{\dot I}_{\mathrm {U}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは