《理論》〈電気回路〉[R03:問4]正弦波交流電源に接続された回路に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，正弦波交流電源に接続された回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

図の回路において，電源から見た回路の合成リアクタンスを\( \ X \ \)と置く。ただし，正弦波交流電源の角周波数は\( \ \omega \ \)とする。

(a)　\( \ \left| {\dot I}_{\mathrm {L}}\right| =\left| {\dot I}_{\mathrm {C}}\right| \ \)が成立するのは\( \ \omega = \ \fbox {　 （１） 　} \ \)のときである。\( \ \omega \ \)が\( \ \fbox {　 （１） 　} \ \)のときの回路の合成インピーダンス\( \ R+\mathrm {j}X \ \)及び電流\( \ {\dot I}_{\mathrm {R}} \ \)を計算すると，\( \ \left| {\dot V}_{\mathrm {R}}\right| = \ \fbox {　 （２） 　} \ \)となる。

(b)　\( \ \displaystyle \frac {1}{\mathrm {j}\omega C}=\frac {R}{\mathrm {j}} \ \)，\( \ \displaystyle \mathrm {j}\omega L=\mathrm {j}\frac {R}{2} \ \)のときは，\( \ \mathrm {j}X= \ \fbox {　 （３） 　} \ \)であり，電流\( \ {\dot I}_{\mathrm {R}} \ \)は\( \ {\dot I}_{\mathrm {R}}= \ \fbox {　 （４） 　} \ \)となる。\( \ {\dot I}_{\mathrm {R}} \ \)が\( \ \fbox {　 （４） 　} \ \)のときの回路が消費する有効電力は\( \ \fbox {　 （５） 　} \ \)となる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\mathrm {j}R　　　　　　　&（ロ）&　\sqrt {LC}　　　　　　　&（ハ）&　0 \\[ 5pt ] &（ニ）&　\frac {\left| \dot E\right| ^{2}}{2R}　　　　　　　&（ホ）&　\mathrm {j}\frac {R}{2}　　　　　　　&（ヘ）&　\frac {\left| \dot E\right| ^{2}}{3R} \\[ 5pt ] &（ト）&　\left| \dot E\right| 　　　　　　　&（チ）&　\frac {\dot E}{\sqrt {3}R}\mathrm {e}^{-\mathrm {j}\frac {\pi }{3}}　　　　　　　&（リ）&　\frac {\dot E}{\sqrt {2}R}\mathrm {e}^{-\mathrm {j}\frac {\pi }{4}} \\[ 5pt ] &（ヌ）&　\frac {\left| \dot E\right| ^{2}}{5R}　　　　　　　&（ル）&　\frac {\dot E}{\sqrt {5}R}\mathrm {e}^{-\mathrm {j}\frac {\pi }{6}}　　　　　　　&（ヲ）&　\frac {1}{\sqrt {LC}} \\[ 5pt ] &（ワ）&　\frac {1}{LC}　　　　　　　&（カ）&　\frac {\left| \dot E\right| }{2}　　　　　　　&（ヨ）&　\mathrm {j}2R \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

交流回路の回路計算に関する問題です。
(2)が少し引っ掛かりやすい問題，(4)が少し数学力が必要となる問題です。
二次試験には同レベルかそれ以上の計算が必要となりますので，一次試験の段階から数学の力は上げて行くようにしましょう。

1.直列回路の共振回路
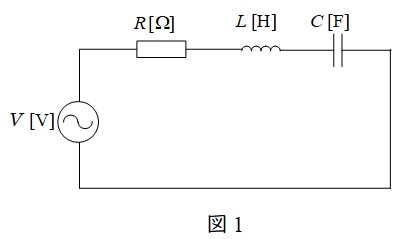
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ] \end{eqnarray}
\] となり，インピーダンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.並列回路の共振回路
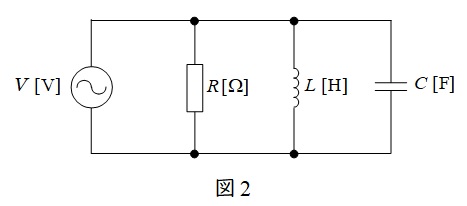
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\] となり，アドミタンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.複素平面における複素数の表記方法
図3のような複素空間上の値\( \ \dot Z =R+\mathrm {j}X \ \)において，以下のような表記方法が定義されます。
ただし，\( \ \dot Z \ \)の絶対値\( \ \left| \dot Z\right| = \sqrt {R^{2}+X^{2}} \ \)，\( \ \dot Z \ \)と実軸となす角を\( \ \theta \ \)とします。

①直交座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \left( \cos \theta +\mathrm {j}\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\]

②指数表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \mathrm {e}^{\mathrm {j}\theta } \\[ 5pt ] \end{eqnarray}
\] ただし，
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ] \end{eqnarray}
\] であり，これをオイラーの公式といいます。

③極座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| ∠\theta \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ヲ
ワンポイント解説「2.並列回路の共振回路」の通り，\( \ \left| {\dot I}_{\mathrm {L}}\right| =\left| {\dot I}_{\mathrm {C}}\right| \ \)が成立するのは，それぞれの素子にかかる電圧を\( \ \dot V \ \)とすると，
\[
\begin{eqnarray}
\left| \mathrm {j}\omega C{\dot V}\right| &=&\left| \frac {\dot V}{\mathrm {j}\omega L}\right| \\[ 5pt ] \left| \mathrm {j}\omega C\right| &=&\left| \frac {1}{\mathrm {j}\omega L}\right| \\[ 5pt ] \omega C&=&\frac {1}{\omega L} \\[ 5pt ] \omega &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ハ
ワンポイント解説「2.並列回路の共振回路」の通り，並列共振状態においては，アドミタンスが零すなわちインピーダンスが\( \ \infty \ \)となるので，回路には電流が流れず\( \ {\dot I}_{\mathrm {R}}=0 \ \mathrm {[A]} \ \)となる。したがって，\( \ R \ \)における電圧降下もなく\( \ \left| {\dot V}_{\mathrm {R}}\right| =0 \ \mathrm {[V]} \ \)と求められる。

(3)解答：イ
\( \ \displaystyle \frac {1}{\mathrm {j}\omega C}=\frac {R}{\mathrm {j}} \ \)，\( \ \displaystyle \mathrm {j}\omega L=\mathrm {j}\frac {R}{2} \ \)のとき，合成リアクタンス\( \ \mathrm {j}X \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X &=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega C}\cdot \mathrm {j}\omega L}{\displaystyle \frac {1}{\mathrm {j}\omega C}+\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {\displaystyle \frac {R}{\mathrm {j}}\cdot \mathrm {j}\frac {R}{2}}{\displaystyle \frac {R}{\mathrm {j}}+\mathrm {j}\frac {R}{2}} \\[ 5pt ] &=&\frac {\displaystyle \frac {R^{2}}{2}}{\displaystyle -\mathrm {j}R+\mathrm {j}\frac {R}{2}} \\[ 5pt ] &=&\frac {\displaystyle \frac {R^{2}}{2}}{\displaystyle -\mathrm {j}\frac {R}{2}} \\[ 5pt ] &=&\mathrm {j}\frac {\displaystyle \frac {R^{2}}{2}}{\displaystyle \frac {R}{2}} \\[ 5pt ] &=&\mathrm {j}R \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：リ
(3)より，\( \ {\dot I}_{\mathrm {R}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {R}} &=&\frac {\dot E}{R+\mathrm {j}R} \\[ 5pt ] &=&\frac {\dot E}{R+\mathrm {j}R}\times \frac {R-\mathrm {j}R}{R-\mathrm {j}R} \\[ 5pt ] &=&\frac {\dot E}{R^{2}+R^{2}}\times \left( R-\mathrm {j}R\right) \\[ 5pt ] &=&\frac {\dot E}{2R^{2}}\times R\left( 1-\mathrm {j}\right) \\[ 5pt ] &=&\frac {\dot E}{2R}\left( 1-\mathrm {j}\right) \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「3.複素平面における複素数の表記方法」により指数表記すると，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {R}} &=&\frac {\dot E}{\sqrt {2}R}\left( \frac {1}{\sqrt {2}}-\mathrm {j}\frac {1}{\sqrt {2}}\right) \\[ 5pt ] &=&\frac {\dot E}{\sqrt {2}R}\left( \cos \frac {\pi }{4}-\mathrm {j}\sin \frac {\pi }{4}\right) \\[ 5pt ] &=&\frac {\dot E}{\sqrt {2}R}\mathrm {e}^{-\mathrm {j}\frac {\pi }{4}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
回路が消費する有効電力\( \ P \ \)は，抵抗\( \ R \ \)で消費される電力であるから，
\[
\begin{eqnarray}
P &=&R\left| {\dot I}_{\mathrm {R}}\right| ^{2} \\[ 5pt ] &=&R\left( \frac {\left| \dot E\right| }{\sqrt {2}R}\right) ^{2} \\[ 5pt ] &=&\frac {\left| \dot E\right| ^{2}}{2R}　 \\[ 5pt ] \end{eqnarray}
\] と求められる。