Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,交流回路の電流計算の方法に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。
図の回路において電流\( \ i(t) \ \)を求めたい。ただし,交流電圧源\( \ e(t)=E_{m} \cos \omega t \ \),\( \ E_{m}=100 \ \mathrm {[V]} \ \),\( \ \omega =10^{5} \ \mathrm {[rad/s]} \ \)とし,コンデンサ\( \ C=1 \ \mathrm {[\mu F]} \ \),抵抗\( \ R=10 \ \mathrm {[\Omega ]} \ \)とする。
まず,電源側からみた回路の複素インピーダンスは\( \ \dot Z= \ \fbox { (1) } \ \)となる。\( \ \dot Z = \left| \dot Z \right| \mathrm {e}^{\mathrm {j}\varphi } \ \)とおき,\( \ \omega \ \),\( \ C \ \),\( \ R \ \)に上記の数値を代入すると\( \ \left| \dot Z \right| = \ \fbox { (2) } \ \mathrm {[\Omega ]} \ \)及び\( \ \varphi =\fbox { (3) } \ \mathrm {[rad]} \ \)となる。したがって,電流を\( \ i(t)=I_{m} \cos \left( 10^{5}t+\theta \right) \ \)とおくと\( \ I_{m}= \ \fbox { (4) } \ \mathrm {[A]} \ \)及び\( \ \theta = \ \fbox { (5) } \ \mathrm {[rad]} \ \)となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& R+\mathrm {j}\omega C+\frac {1}{R+\mathrm {j}\omega C} &(ロ)& 7.1 &(ハ)& -\frac {\pi }{3} \\[ 5pt ]
&(ニ)& 21.2 &(ホ)& 3.33 &(ヘ)& \frac {\pi }{4} \\[ 5pt ]
&(ト)& -\frac {\pi }{2} &(チ)& 5.77 &(リ)& -\frac {\pi }{4} \\[ 5pt ]
&(ヌ)& 4.71 &(ル)& \frac {\pi }{2} &(ヲ)& \frac {1+\mathrm {j}\omega CR}{\mathrm {j}\omega C}+\frac {R}{1+\mathrm {j}\omega CR} \\[ 5pt ]
&(ワ)& 30 &(カ)& \frac {R+\mathrm {j}\omega C}{\mathrm {j}\omega CR}+\frac {R}{1+\mathrm {j}\omega CR} &(ヨ)& \frac {\pi }{3} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
抵抗とコンデンサを直並列接続した回路のインピーダンスや電圧・電流の瞬時値の考え方を問う問題です。
後半の(4)及び(5)の解法に迷うところですが,ここでは問題に合わせ指数関数で計算を行っています。慣れてくればもう少し早く解ける方法も見つかるかもしれませんので,解答例だけに囚われず,ご自身なりの解き方を磨いていってください。
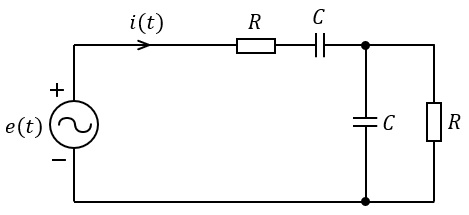
1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンスは,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,それぞれの電圧と電流の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ]
{\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ]
{\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
となります。この関係をベクトル図に表すと,図1~図3となります。
2.合成インピーダンス
インピーダンス\( \ {\dot Z}_{1} \ \mathrm {[\Omega ]} \ \)と\( \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時,直列及び並列の合成インピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。
①直列
直列合成インピーダンス\( \ {\dot Z} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}&=&{\dot Z}_{1}+{\dot Z}_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成インピーダンス\( \ {\dot Z} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\frac {1}{{\dot Z}}&=&\frac {1}{{\dot Z}_{1}}+\frac {1}{{\dot Z}_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
{\dot Z}&=&\frac {{\dot Z}_{1}{\dot Z}_{2}}{{\dot Z}_{1}+{\dot Z}_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.複素平面における複素数の表記方法
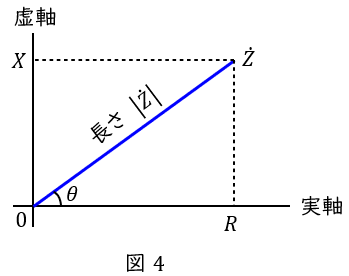
図4のような複素空間上の値\( \ \dot Z =R+\mathrm {j}X \ \)において,以下のような表記方法が定義されます。
ただし,\( \ \dot Z \ \)の絶対値\( \ \left| \dot Z\right| = \sqrt {R^{2}+X^{2}} \ \),\( \ \dot Z \ \)と実軸となす角を\( \ \theta \ \)とします。
①直交座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \left( \cos \theta +\mathrm {j}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
②指数表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \mathrm {e}^{\mathrm {j}\theta } \\[ 5pt ]
\end{eqnarray}
\]
ただし,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これをオイラーの公式といいます。
③極座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| ∠\theta \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ヲ
回路の右側の\( \ C \ \)と\( \ R \ \)の合成インピーダンス\( \ {\dot Z}_{1} \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」及び「2.合成インピーダンス」の通り,
\[
\begin{eqnarray}
{\dot Z}_{1}&=&\frac {\displaystyle R\cdot \frac {1}{\mathrm {j}\omega C}}{\displaystyle R+\frac {1}{\mathrm {j}\omega C}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {R}{\mathrm {j}\omega C}}{\displaystyle \frac {1+\mathrm {j}\omega CR}{\mathrm {j}\omega C}} \\[ 5pt ]
&=&\frac {R}{1+\mathrm {j}\omega CR} \\[ 5pt ]
\end{eqnarray}
\]
となるので,回路全体のインピーダンス\( \ {\dot Z} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\dot Z&=&R+\frac {1}{\mathrm {j}\omega C}+{\dot Z}_{1} \\[ 5pt ]
&=&\frac {1+\mathrm {j}\omega CR}{\mathrm {j}\omega C}+\frac {R}{1+\mathrm {j}\omega CR} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
(1)解答式に各値を代入すると,
\[
\begin{eqnarray}
\dot Z&=&\frac {1+\mathrm {j}10^{5}\times 1\times 10^{-6}\times 10}{\mathrm {j}10^{5}\times 1\times 10^{-6}}+\frac {10}{1+\mathrm {j}10^{5}\times 1\times 10^{-6}\times 10} \\[ 5pt ]
&=&\frac {1+\mathrm {j}}{\mathrm {j}0.1}+\frac {10}{1+\mathrm {j}} \\[ 5pt ]
&=&\frac {10+\mathrm {j}10}{\mathrm {j}}+\frac {10}{1+\mathrm {j}}\times \frac {1-\mathrm {j}}{1-\mathrm {j}} \\[ 5pt ]
&=&-\mathrm {j}\left( 10+\mathrm {j}10\right) +\frac {10-\mathrm {j}10}{1+1} \\[ 5pt ]
&=&10-\mathrm {j}10+5-\mathrm {j}5 \\[ 5pt ]
&=&15-\mathrm {j}15 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
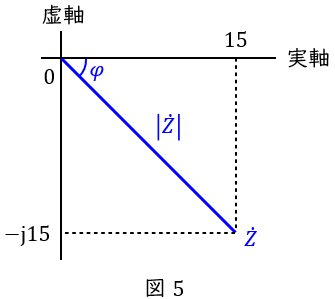
となるので,複素平面上で表すと図5のようになる。したがって,\( \ \dot Z \ \mathrm {[\Omega ]} \ \)の大きさ\( \ \left| \dot Z \right| \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\left| \dot Z \right|&=&\sqrt {15^{2}+15^{2}} \\[ 5pt ]
&≒&21.21 → 21.2 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
図5より,\( \ \displaystyle \varphi =-\frac {\pi }{4} \ \mathrm {[rad]} \ \)と求められる。
(4)解答:ヌ
交流電圧源の瞬時値\( \ e\left( t \right) \ \)は,
\[
\begin{eqnarray}
e\left( t \right) &=&E_{m} \cos \omega t \\[ 5pt ]
&=&100 \cos 10^{5} t \\[ 5pt ]
\end{eqnarray}
\]
であるため,電圧を基準として指数関数表記すると,ワンポイント解説「3.複素平面における複素数の表記方法」の通り,
\[
\begin{eqnarray}
\dot E&=&\frac {100}{\sqrt {2}}\mathrm {e}^{\mathrm {j}0} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,電流\( \ \dot I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
\dot I&=&\frac {\dot E}{\dot Z} \\[ 5pt ]
&=&\frac {\displaystyle \frac {100}{\sqrt {2}}\mathrm {e}^{\mathrm {j}0}}{21.21\mathrm {e}^{-\mathrm {j}\frac {\pi }{4}}} \\[ 5pt ]
&≒&3.334\mathrm {e}^{\mathrm {j}\frac {\pi }{4}} \\[ 5pt ]
\end{eqnarray}
\]
となり,電流波高値\( \ I_{m} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{m}&=&3.334\times \sqrt {2} \\[ 5pt ]
&≒&4.71 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヘ
(4)より,\( \ \dot I=3.334\mathrm {e}^{\mathrm {j}\frac {\pi }{4}} \ \mathrm {[A]} \ \)であるから,\( \ \displaystyle \theta =\frac {\pi }{4} \ \mathrm {[rad]} \ \)と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは