《理論》〈電気回路〉[R03:問3]重ね合わせの理を用いた直流回路の解法に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

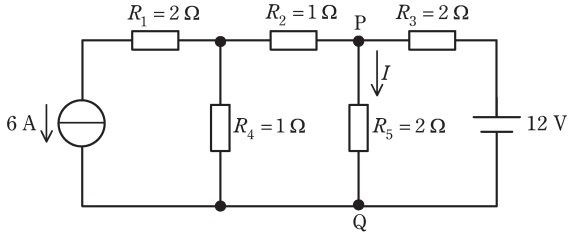
図の直流回路において，重ね合わせの理を用いて抵抗$ \ R_{\mathrm {5}} \ $を流れる電流$ \ I \ $について解析する。ただし，抵抗$ \ R_{\mathrm {5}} \ $に流れる電流の正方向を図中の節点$ \ \mathrm {P} \ $から$ \ \mathrm {Q} \ $の向きとする。

重ね合わせの理は，$ \ \fbox {　（１）　} \ $回路において成立する定理である。図の回路において，電圧源を残して電流源を取り除いた回路を考え，抵抗$ \ R_{\mathrm {5}} \ $に流れる電流$ \ I_{\mathrm {a}} \ $を求めれば，$ \ I_{\mathrm {a}}= \ \fbox {　（２）　} \ \mathrm {A} \ $となる。このとき，電流源は$ \ \fbox {　（３）　} \ $除去されている。

次に，図の回路において，電流源を残して電圧源を取り除いた回路を考え，抵抗$ \ R_{\mathrm {5}} \ $に流れる電流$ \ I_{\mathrm {b}} \ $を求めた上で，電流$ \ I_{\mathrm {a}} \ $と$ \ I_{\mathrm {b}} \ $を重ね合わせれば，抵抗$ \ R_{\mathrm {5}} \ $に流れる電流は$ \ I= \ \fbox {　（４）　} \ \mathrm {A} \ $と求められる。

また，図の回路において，電圧源の電圧を$ \ \fbox {　（５）　} \ \mathrm {V} \ $とすれば，抵抗$ \ R_{\mathrm {5}} \ $に流れる電流は$ \ I= 0 \ \mathrm {A} \ $となる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　短絡　　　　　　　&（ロ）&　-1　　　　　　　&（ハ）&　8 \\[ 5pt ] &（ニ）&　6　　　　　　　&（ホ）&　線形　　　　　　　&（ヘ）&　-2 \\[ 5pt ] &（ト）&　1　　　　　　　&（チ）&　2　　　　　　　&（リ）&　能動 \\[ 5pt ] &（ヌ）&　非線形　　　　　　　&（ル）&　接地　　　　　　　&（ヲ）&　-3 \\[ 5pt ] &（ワ）&　開放　　　　　　　&（カ）&　3　　　　　　　&（ヨ）&　4 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

直流回路に関する問題です。
(1)～(4)はかなり基礎的な内容，(5)のみ$ \ 2 \ $種らしい問題かと思います。
直流回路の問題は$ \ 3 \ $種とそれほど難易度は変わらないため，合格に向けては確実に得点できるようにしておきましょう。

1.重ね(重ね合わせ)の理
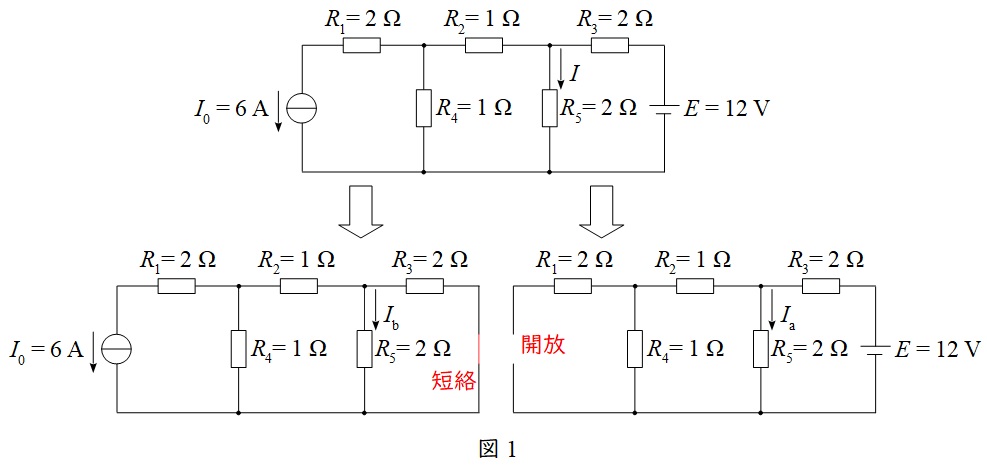
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。
したがって，本問の回路は図1のように分けて考えることができます。

【解答】

(1)解答：ホ
題意より解答候補は，（ホ）線形，（リ）能動，（ヌ）非線形，（ル）接地，になると思います。
重ね合わせの理は抵抗値が状態によって変化しない，すなわち電流と電圧が比例する線形回路において成立する定理となります。

(2)解答：チ
図1右の回路において，$ \ R_{1} \ $には電流が流れないため，無視して考える。
$ \ R_{2} \ $，$ \ R_{3} \ $，$ \ R_{4} \ $，$ \ R_{5} \ $の合成抵抗$ \ R \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
R &=&R_{3}+\frac {\left( R_{2}+R_{4}\right) R_{5}}{\left( R_{2}+R_{4}\right) +R_{5}} \\[ 5pt ] &=&2+\frac {\left( 1+1\right) \times 2}{\left( 1+1\right) +2} \\[ 5pt ] &=&3 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，電圧源$ \ E=12 \ \mathrm {[V]} \ $を流れる電流$ \ I_{1} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{1} &=&\frac {E}{R} \\[ 5pt ] &=&\frac {12}{3} \\[ 5pt ] &=&4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，$ \ R_{5} \ $を流れる電流$ \ I_{\mathrm {a}} \ \mathrm {[A]} \ $は，分流の法則より，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\frac {R_{2}+R_{4}}{\left( R_{2}+R_{4}\right) +R_{5}}I_{1} \\[ 5pt ] &=&\frac {1+1}{\left( 1+1\right) +2}\times 4 \\[ 5pt ] &=&2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
題意より解答候補は，（イ）短絡，（ワ）開放，になると思います。
ワンポイント解説「1.重ね(重ね合わせ)の理」の通り，電流源は開放します。

(4)解答：ト
図1左の回路において，$ \ R_{2} \ $，$ \ R_{3} \ $，$ \ R_{5} \ $の合成抵抗$ \ R^{\prime } \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
R^{\prime } &=&R_{2}+\frac {R_{3}R_{5}}{R_{3}+R_{5}} \\[ 5pt ] &=&1+\frac {2\times 2}{2+2} \\[ 5pt ] &=&2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，電流源$ \ I_{0}=6 \ \mathrm {[A]} \ $から$ \ \mathrm {Q} \ $側へ流れる電流$ \ I_{2} \ \mathrm {[A]} \ $は，分流の法則より，
\[
\begin{eqnarray}
I_{2} &=&\frac {R_{4}}{R_{4}+R^{\prime }}I_{0} \\[ 5pt ] &=&\frac {1}{1+2}\times 6 \\[ 5pt ] &=&2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，$ \ R_{5} \ $を流れる電流$ \ I_{\mathrm {b}} \ \mathrm {[A]} \ $は，電流の向きに注意すると，
\[
\begin{eqnarray}
I_{\mathrm {b}} &=&-\frac {R_{3}}{R_{3}+R_{5}}I_{2} \\[ 5pt ] &=&-\frac {2}{2+2}\times 2 \\[ 5pt ] &=&-1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ I_{\mathrm {a}} \ $と$ \ I_{\mathrm {b}} \ $を重ね合わせれば$ \ I \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I &=&I_{\mathrm {a}}+I_{\mathrm {b}} \\[ 5pt ] &=&2-1 \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
$ \ R_{5} \ $に電流が流れないためには，(2)の電流$ \ I_{\mathrm {a}} \ $が$ \ 1 \ \mathrm {A} \ $となればよい。
(2)と同様に，電圧源$ \ E \ \mathrm {[V]} \ $を流れる電流$ \ I_{1}^{\prime } \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{1}^{\prime } &=&\frac {E}{R} \\[ 5pt ] &=&\frac {E}{3} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，$ \ R_{5} \ $を流れる電流$ \ I_{\mathrm {a}} \ \mathrm {[A]} \ $は，分流の法則より，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\frac {R_{2}+R_{4}}{\left( R_{2}+R_{4}\right) +R_{5}}I_{1}^{\prime } \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
1&=&\frac {1+1}{\left( 1+1\right) +2}\cdot \frac {E}{3} \\[ 5pt ] 1&=&\frac {1}{2}\cdot \frac {E}{3} \\[ 5pt ] E&=&6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。