Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,相互インダクタンスに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。
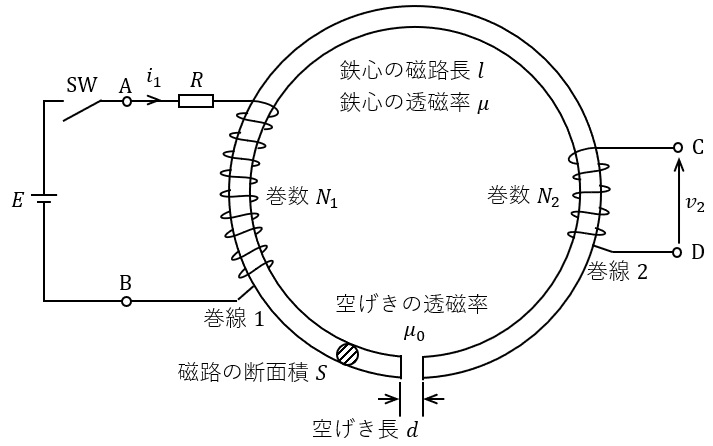
図のように,空げきをもつ環状鉄心に,巻数\( \ N_{1} \ \)の巻線\( \ 1 \ \)及び巻数\( \ N_{2} \ \)の巻線\( \ 2 \ \)が巻かれている。鉄心部は,磁路長\( \ l \ \),透磁率\( \ \mu \ \)の鉄心から成っている。また,空げき部の長さは\( \ d \ \)で,その透磁率は\( \ \mu _{0} \ \)である。磁路の断面積はいずれの部分も\( \ S \ \)である。磁路において磁束は一様に分布し,飽和,ヒステリシス,渦電流,漏れ磁束,空げき部の端効果はないものとする。巻線\( \ 1 \ \)は,電圧が\( \ E \ \)の直流電源にスイッチ\( \ \mathrm {SW} \ \)を経て図のように接続されている。抵抗\( \ R \ \)は巻線\( \ 1 \ \)の抵抗である。
鉄心部及び空げき部から成る磁路は巻線\( \ 1 \ \)及び巻線\( \ 2 \ \)に共通に鎖交する磁束(相互磁束)を通す磁路であるが,その磁気抵抗は\( \ \fbox { (1) } \ \)である。巻線\( \ 2 \ \)の自己インダクタンス及び両巻線間の相互インダクタンスは,巻線\( \ 1 \ \)のインダクタンスのそれぞれ\( \ \fbox { (2) } \ \)倍となる。
いま,時刻\( \ t=0 \ \)でスイッチ\( \ \mathrm {SW} \ \)を投入したとする。両巻線間の相互インダクタンスを巻線\( \ 2 \ \)に生じる電圧から求めてみよう。まず,巻線\( \ 1 \ \)に流れる電流\( \ i_{1} \ \)により巻線\( \ 2 \ \)に発生する電圧\( \ v_{2} \ \)(端子\( \ \mathrm {D} \ \)を基準とした端子\( \ \mathrm {C} \ \)の電位)は,両巻線間の相互インダクタンスを\( \ M \ \)とするとき,\( \ v_{2}= \ \fbox { (3) } \ \)となる。この電圧\( \ v_{2} \ \)を時間について\( \ t=0 \ \)から無限大まで積分すると,
\[
\begin{eqnarray}
\int _{0}^{\infty } v_{2}\mathrm {d}t&=&\int _{0}^{ \ \fbox { (4) } \ } M\mathrm {d}i_{1} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,右辺の積分の上限は電流\( \ i_{1} \ \)の最終値であり,\( \ \fbox { (4) } \ \)である。この式より,相互インダクタンス\( \ M \ \)は,
\[
\begin{eqnarray}
M&=& \ \fbox { (5) } \ \times \int _{0}^{\infty } v_{2}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& M\frac {\mathrm {d}i_{1}}{\mathrm {d}t} &(ロ)& \frac {S}{\mu l}+\frac {S}{\mu _{0}d} &(ハ)& N_{2} \ 及び \ {N_{2}}^{2} \\[ 5pt ]
&(ニ)& \frac {M}{R} &(ホ)& \left( \frac {N_{2}}{N_{1}}\right) ^{2} \ 及び \ \frac {N_{2}}{N_{1}} &(ヘ)& 1 \\[ 5pt ]
&(ト)& \frac {M}{R}\frac {\mathrm {d}i_{1}}{\mathrm {d}t} &(チ)& \frac {l}{\mu S}+\frac {d}{\mu _{0}S} &(リ)& \frac {E}{R} \\[ 5pt ]
&(ヌ)& RE &(ル)& \frac {\mu S}{l}+\frac {\mu _{0}S}{d} &(ヲ)& 0 \\[ 5pt ]
&(ワ)& \left( \frac {N_{1}}{N_{2}}\right) ^{2} \ 及び \ \frac {N_{1}}{N_{2}} &(カ)& \frac {R}{E} &(ヨ)& \frac {ME}{R}\frac {\mathrm {d}i_{1}}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
磁気回路と相互インダクタンスを検討する問題です。
公式丸暗記に留まらず,しっかりと内容を理解しているかを問う\( \ 2 \ \)種らしい問題です。本問でおそらく最も難易度が高いのは(2)で,(2)ができなくても(3)以降は解けますので,諦めずに解くようにして下さい。
1.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)
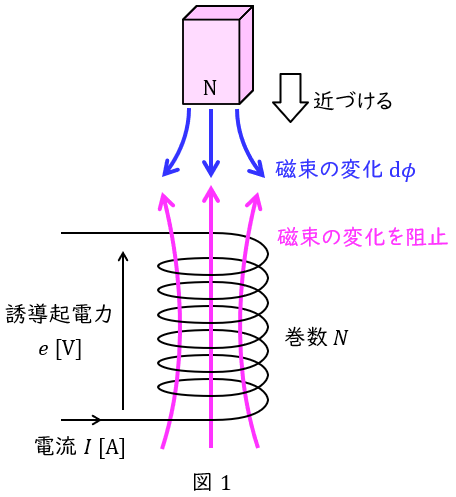
図1に示すように,巻数\( \ N \ \)のコイルを貫通する磁束\( \ \phi \ \mathrm {[Wb]} \ \)があるとき,コイルに発生する誘導起電力\( \ e \ \mathrm {[V]} \ \)は,磁束の時間変化\( \ \displaystyle \frac {\mathrm {d} \phi }{\mathrm {d} t} \ \)に比例し,
\[
\begin{eqnarray}
e&=&−N\frac {\mathrm {d} \phi }{\mathrm {d} t} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。これをファラデーの電磁誘導の法則といいます。一方,電流変化\( \ \displaystyle \frac {\mathrm {d} I }{\mathrm {d} t} \ \)を考える場合,
\[
\begin{eqnarray}
e&=&−L\frac {\mathrm {d} I }{\mathrm {d} t} \\[ 5pt ]
\end{eqnarray}
\]
という関係も成り立ち,\( \ L \ \mathrm {[H]}\ \)を自己インダクタンスと言います。これらの関係から,
\[
\begin{eqnarray}
−N\frac {\mathrm {d} \phi }{\mathrm {d} t}&=&−L\frac {\mathrm {d} I }{\mathrm {d} t} \\[ 5pt ]
N\phi &=&LI \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
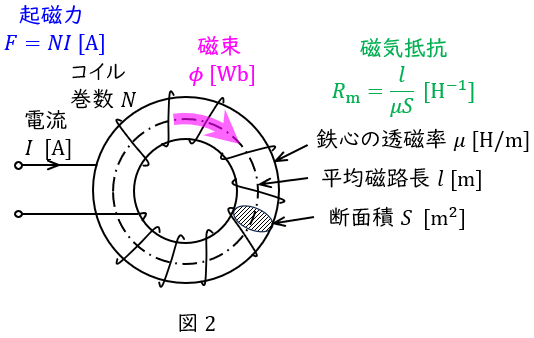
2.磁気回路のオームの法則
中心長さ\( \ l \ \mathrm {[ m ]} \ \)の環状鉄心に巻数\( \ N \ \)のコイルが巻かれ,そこに電流\( \ I \ \mathrm {[ A ]} \ \)が流れている時,鉄心内の磁界の強さ\( \ H \ \mathrm {[ A / m ]} \ \)は,アンペールの周回積分の法則より,
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ]
H&=&\frac {NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
であるから,鉄心内の磁束密度\( \ B \ \mathrm {[ T ]} \ \)は,鉄心内の透磁率\( \ \mu \ \mathrm {[ H / m ]} \ \)とすると,
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ]
&=&\frac {\mu NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
となります。鉄心内の磁束\( \ \phi \ \mathrm {[ Wb ]} \ \)は,鉄心の断面積\( \ S \ \mathrm {[ m^{2} ]} \ \)とすると,
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ]
&=&\frac {\mu NIS}{l} \\[ 5pt ]
&=&\frac {NI}{\displaystyle \frac {l}{\mu S}} \\[ 5pt ]
\end{eqnarray}
\]
となり,起磁力\( \ F=NI \ \mathrm {[ A ]} \ \),磁気抵抗\( \ R_{\mathrm {m}}=\displaystyle \frac {l}{\mu S} \ \mathrm {[ H^{-1} ]} \ \)とすると,
\[
\begin{eqnarray}
\phi &=&\frac {F}{R_{\mathrm {m}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,磁気回路のオームの法則が成立します。また,このときの自己インダクタンス\( \ L \ \mathrm {[H]} \ \)は,
\[
\begin{eqnarray}
L &=&\frac {N\phi }{I} \\[ 5pt ]
&=&\frac {\displaystyle N\cdot \frac {NI}{R_{\mathrm {m}}}}{I} \\[ 5pt ]
&=&\frac {N^{2}}{R_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {N^{2}}{\displaystyle \frac {l}{\mu S} } \\[ 5pt ]
&=&\frac {\mu SN^{2}}{l} \\[ 5pt ]
\end{eqnarray}
\]
となります。
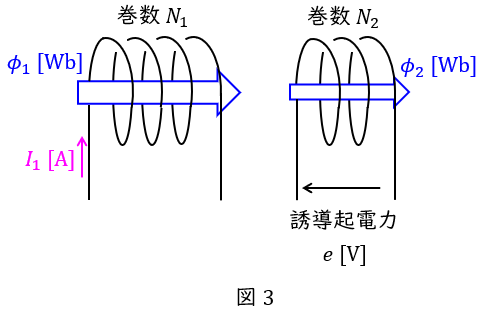
3.相互インダクタンス\( \ M \ \)
図3に示すように,巻数\( \ N_{1} \ \)のコイルと巻数\( \ N_{2} \ \)のコイルが近傍にあり,巻数\( \ N_{1} \ \)のコイルに流れる電流が\( \ \displaystyle \frac {\mathrm {d}I_{1}}{\mathrm {d}t} \ \mathrm {[A / s]} \ \)変化し,貫通する磁束が\( \ \displaystyle \frac {\mathrm {d}\phi _{1}}{\mathrm {d}t} \ \mathrm {[Wb / s]} \ \)変化すると,巻数\( \ N_{2} \ \)のコイルの磁束も変化します。このときの磁束の変化量を\( \ \displaystyle \frac {\mathrm {d}\phi _{2}}{\mathrm {d}t} \ \mathrm {[Wb / s]}\left( \phi _{1}≧\phi _{2}\right) \ \)とすると,巻数\( \ N_{2} \ \)のコイルに発生する誘導起電力\( \ e \ \mathrm {[V]} \ \)は,ファラデーの電磁誘導の法則から,
\[
\begin{eqnarray}
e&=&−N_{2}\frac {\mathrm {d} \phi _{2}}{\mathrm {d} t} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,電流変化\( \ \displaystyle \frac {\mathrm {d}I_{1}}{\mathrm {d}t} \ \mathrm {[A / s]} \ \)を考える場合,
\[
\begin{eqnarray}
e&=&-M\frac {\mathrm {d} I _{1}}{\mathrm {d} t} \\[ 5pt ]
\end{eqnarray}
\]
という関係も成り立ち,\( \ M \ \mathrm {[H]} \ \)を相互インダクタンスと言います。これらの関係から,
\[
\begin{eqnarray}
−N_{2}\frac {\mathrm {d} \phi _{2}}{\mathrm {d} t}&=&−M\frac {\mathrm {d} I_{1} }{\mathrm {d} t} \\[ 5pt ]
N_{2}\phi _{2}&=&MI_{1} \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
【解答】
(1)解答:チ
磁気抵抗\( \ R_{m} \ \)は,ワンポイント解説「2.磁気回路のオームの法則」の通り,
\[
\begin{eqnarray}
R_{m} &=&\frac {l}{\mu S}+\frac {d}{\mu _{0}S} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ホ
ワンポイント解説「1.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)」,「2.磁気回路のオームの法則」,「3.相互インダクタンス\( \ M \ \)」の通り,各自己インダクタンスと相互インダクタンスは,漏れ磁束がないことに注意すると,
\[
\begin{eqnarray}
L_{1}I_{1} &=&N_{1}\phi_{1} \\[ 5pt ]
&=&N_{1}\frac {N_{1}I_{1}}{R_{m}} \\[ 5pt ]
L_{1}&=&\frac {{N_{1}}^{2}}{R_{m}} \\[ 5pt ]
L_{2}I_{2} &=&N_{2}\phi_{2} \\[ 5pt ]
&=&N_{2}\frac {N_{2}I_{2}}{R_{m}} \\[ 5pt ]
L_{2}&=&\frac {{N_{2}}^{2}}{R_{m}} \\[ 5pt ]
MI_{1} &=&N_{2}\phi_{2} \\[ 5pt ]
&=&N_{2}\phi_{1} \\[ 5pt ]
&=&N_{2}\frac {N_{1}I_{1}}{R_{m}} \\[ 5pt ]
M&=&\frac {N_{1}N_{2}}{R_{m}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\frac {L_{2}}{L_{1}} &=&\frac {\displaystyle \frac {{N_{2}}^{2}}{R_{m}}}{\displaystyle \frac {{N_{1}}^{2}}{R_{m}}} \\[ 5pt ]
&=&\frac {{N_{2}}^{2}}{{N_{1}}^{2}} \\[ 5pt ]
\frac {M}{L_{1}} &=&\frac {\displaystyle \frac {N_{1}N_{2}}{R_{m}}}{\displaystyle \frac {{N_{1}}^{2}}{R_{m}}} \\[ 5pt ]
&=&\frac {N_{2}}{N_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:イ
ワンポイント解説「3.相互インダクタンス\( \ M \ \)」の通り,巻線\( \ 1 \ \)に流れる電流\( \ i_{1} \ \)により巻線\( \ 2 \ \)に発生する電圧\( \ v_{2} \ \)は,
\[
\begin{eqnarray}
v_{2} &=&M\frac {\mathrm {d}i_{1}}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:リ
電流\( \ i_{1} \ \)の最終値,すなわち定常状態において,コイルは短絡状態と考えて良いから,
\[
\begin{eqnarray}
i_{1} &=&\frac {E}{R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
(4)より,
\[
\begin{eqnarray}
\int _{0}^{\infty } v_{2}\mathrm {d}t&=&\int _{0}^{\frac {E}{R}} M\mathrm {d}i_{1} \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,右辺を積分して整理していくと,
\[
\begin{eqnarray}
\int _{0}^{\infty } v_{2}\mathrm {d}t&=&\int _{0}^{\frac {E}{R}} M\mathrm {d}i_{1} \\[ 5pt ]
&=&M\int _{0}^{\frac {E}{R}} \mathrm {d}i_{1} \\[ 5pt ]
&=&M \left[ i_{1}\right] _{0}^{\frac {E}{R}} \\[ 5pt ]
&=&M \times \frac {E}{R} \\[ 5pt ]
M&=&\frac {R}{E}\times \int _{0}^{\infty } v_{2}\mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは