《理論》〈電気回路〉[H19:問2]ノートンの定理を用いた直流回路の演算に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，直流回路の電圧計算の方法に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる数値を解答群の中から選び，その記号をマークシートに記入しなさい。

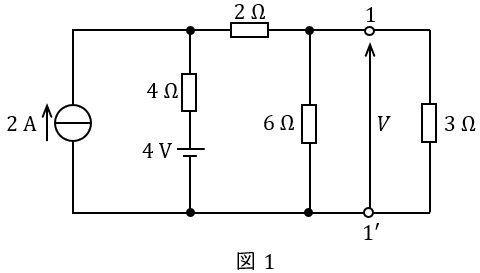
図1に示す回路において，電圧\( \ V \ \mathrm {[V]} \ \)をノートンの定理を用いて求めたい。

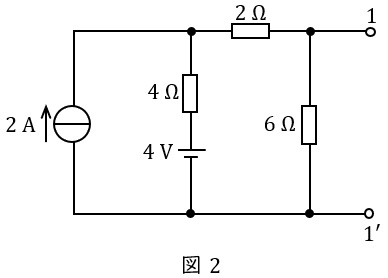
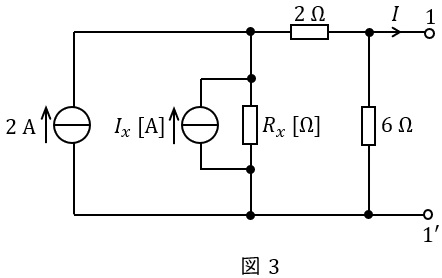
まず，\( \ 3 \ \mathrm {[\Omega ]} \ \)の抵抗を取り去った図2の回路について考える。この回路において\( \ 4 \ \mathrm {[\Omega ]} \ \)の抵抗と\( \ 4 \ \mathrm {[V]} \ \)の電圧源の直列接続は，\( \ R_{x}= \ \fbox {　 （１） 　} \ \mathrm {[\Omega ]} \ \)の抵抗と\( \ I_{x}= \ \fbox {　 （２） 　} \ \mathrm {[A]} \ \)の電流源の並列接続に等価的に変換されるから，図2の回路は図3の回路と等価になる。図3の回路において，端子\( \ 1-1^{\prime } \ \)を短絡したときに流れる電流\( \ I \ \)を求めると\( \ \fbox {　 （３） 　} \ \mathrm {[A]} \ \)となる。

次に，図3の回路内のすべての電流源を零とし，端子\( \ 1-1^{\prime } \ \)からみたコンダクタンスを求めると\( \ \fbox {　 （４） 　} \ \mathrm {[S]} \ \)となる。

以上をもとにノートンの定理を使い，端子\( \ 1-1^{\prime } \ \)に\( \ 3 \ \mathrm {[\Omega ]} \ \)の抵抗を接続したときに端子\( \ 1^{\prime } \ \)を基準とした端子\( \ 1 \ \)の電圧\( \ V \ \)は\( \ \fbox {　 （５） 　} \ \mathrm {[V]} \ \)となる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　6　　　　　&（ロ）&　1.5　　　　　&（ハ）&　3.5 \\[ 5pt ] &（ニ）&　\frac {1}{2}　　　　　&（ホ）&　2　　　　　&（ヘ）&　\frac {1}{4} \\[ 5pt ] &（ト）&　5　　　　　&（チ）&　7　　　　　&（リ）&　9 \\[ 5pt ] &（ヌ）&　3　　　　　&（ル）&　\frac {1}{3}　　　　　&（ヲ）&　4.5 \\[ 5pt ] &（ワ）&　4　　　　　&（カ）&　2.5　　　　　&（ヨ）&　1 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ノートンの定理を用いた回路の演算に関する問題です。
本問に関しては問題文にヒントが与えられているため，ノートンの定理を知らなくてもなんとかなります。諦めずに解くようにしましょう。ノートンの定理はテブナンの定理と合わせて理解すると良いかと思います。

1.テブナンの定理
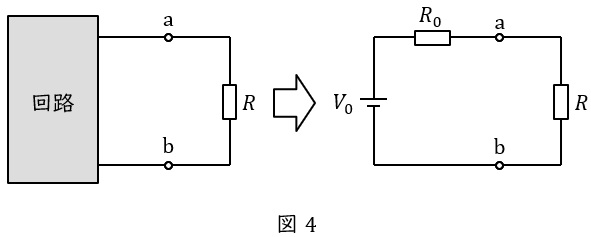
図4のように複雑な回路を電圧源\( \ V_{0} \ \mathrm {[V]} \ \)と抵抗\( \ R_{0} \ \mathrm {[\Omega ]} \ \)に置き換える方法です。
\( \ V_{0} \ \mathrm {[V]} \ \)は端子\( \ \mathrm {a} \ – \ \mathrm {b} \ \)の開放電圧，\( \ R_{0} \ \mathrm {[\Omega ]} \ \)は端子\( \ \mathrm {a} \ – \ \mathrm {b} \ \)から電源側回路を見た合成抵抗となります。
ただし，\( \ R_{0} \ \mathrm {[\Omega ]} \ \)を求める際，電圧源は短絡，電流源は開放します。

2.ノートンの定理
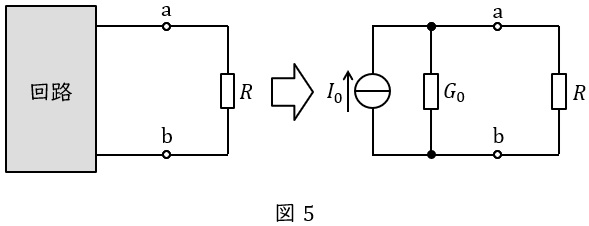
図5のように複雑な回路を電流源\( \ I_{0} \ \mathrm {[A]} \ \)とコンダクタンス\( \ G_{0} \ \mathrm {[S]} \ \)（抵抗の逆数）に置き換える方法です。
\( \ I_{0} \ \mathrm {[A]} \ \)は端子\( \ \mathrm {a} \ – \ \mathrm {b} \ \)を短絡したときの短絡電流，\( \ G_{0} \ \mathrm {[S]} \ \)は端子\( \ \mathrm {a} \ – \ \mathrm {b} \ \)から電源側回路を見た合成コンダクタンスとなります。
ただし，\( \ G_{0} \ \mathrm {[S]} \ \)を求める際，電圧源は短絡，電流源は開放します。

3.電圧源と電流源の等価変換
図6に示すように，電圧源と電流源は抵抗との直列接続と並列接続で等価変換をすることができます。
電圧源の電圧\( \ E \ \mathrm {[V]} \ \)と電流源の電流\( \ I \ \mathrm {[A]} \ \)には，
\[
\begin{eqnarray}
E &=&rI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ワ
ワンポイント解説「3.電圧源と電流源の等価変換」の通り，\( \ R_{x}= 4 \ \mathrm {[\Omega ]} \ \)と求められる。

(2)解答：ヨ
ワンポイント解説「3.電圧源と電流源の等価変換」の通り，
\[
\begin{eqnarray}
I_{x} &=&\frac {4}{4} \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ホ
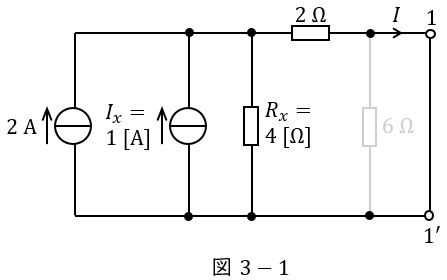
図3の回路において，端子\( \ 1-1^{\prime } \ \)を短絡したときの回路は図3-1の通りとなる。図3-1に分流の法則を適用すると，
\[
\begin{eqnarray}
I &=&\frac {R_{x}}{R_{x}+2}\left( 2+I_{x}\right) \\[ 5pt ] &=&\frac {4}{4+2}\times \left( 2+1\right) \\[ 5pt ] &=&2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
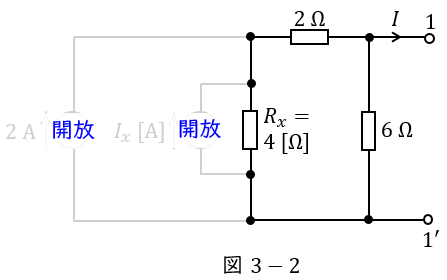
図3の回路において，回路内のすべての電流源を零（開放）としたときの回路は図3-2のようになる。図3-2より，端子\( \ 1-1^{\prime } \ \)からみたコンダクタンス\( \ G_{0} \ \mathrm {[S]} \ \)は，
\[
\begin{eqnarray}
G_{0} &=&\frac {1}{R_{x}+2}+\frac {1}{6} \\[ 5pt ] &=&\frac {1}{4+2}+\frac {1}{6} \\[ 5pt ] &=&\frac {1}{3} \ \mathrm {[S]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
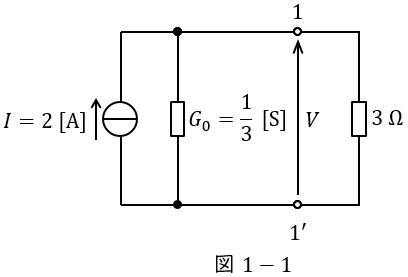
ワンポイント解説「2.ノートンの定理」の通り，図1の回路を等価変換すると図1-1の通りとなる。図1-1に分流の法則を適用すると，\( \ 3 \ \mathrm {\Omega } \ \)の抵抗に流れる電流の大きさ\( \ I^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I^{\prime } &=&\frac {\displaystyle \frac {1}{G_{0}}}{\displaystyle \frac {1}{G_{0}}+3}I \\[ 5pt ] &=&\frac {3}{3+3}\times 2 \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，電圧\( \ V \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V &=&3\times I^{\prime } \\[ 5pt ] &=&3\times 1 \\[ 5pt ] &=&3 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。