《理論》〈電磁気〉[H28:問1] 自己インダクタンスに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，同軸線路の自己インダクタンスに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。なお，同軸線路を構成する導体間の隙間は空気で満たされており，その透磁率は$ \ \mu _{0} \ $である。

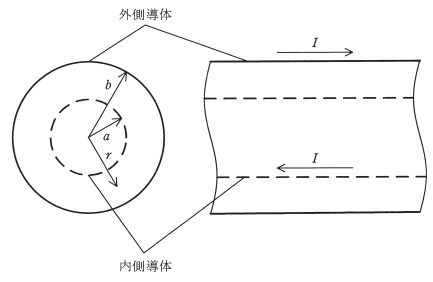
図のように，中心軸を同じくする半径$ \ a \ $の無限に長い円筒状導体(内部導体)と半径$ \ b \ $の無限に長い円筒状導体(外部導体)がある。なお，$ \ a ＜ b \ $であり，それぞれの円筒状導体の厚みは無限に小さいとしてよい。このような回路の単位長さ当たりの自己インダクタンスを，鎖交する磁束を用いる方法と，蓄積される磁気エネルギーを用いる方法の二通りの方法で求める。
同軸線路には，図に示す方向に同じ大きさの電流$ \ I \ $が流れている。この電流が作り出す磁束密度の大きさ$ \ B \ $は，内側導体の内部及び外側導体の外部では零，内側導体及び外側導体に挟まれた領域では$ \ B=\fbox {　（１）　} \ $となるため，単位長さ当たりの鎖交磁束$ \ \Phi \ $は，
\[
\begin{eqnarray}
\Phi &=&\int ^{b}_{a}B\mathrm {d}r=\fbox {　（２）　} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ \Phi \ $と単位長さ当たりの自己インダクタンス$ \ L \ $との関係式$ \ \Phi =\fbox {　（３）　} \ $を用いて，$ \ L \ $が求まる。
一方，単位長さ当たりに蓄積される磁気エネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W &=&2\pi \int ^{b}_{a} \frac {B^{2}}{2\mu _{0}} r\mathrm {d}r=\fbox {　（４）　} \\[ 5pt ] \end{eqnarray}
\] となり，蓄積エネルギーと自己インダクタンスの関係式$ \ W=\fbox {　（５）　} \ $を用いると同様に単位長さ当たりの自己インダクタンスが求まり，両者が一致することが分かる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {I}{L}　　　&（ロ）&　\frac {\mu _{0}I}{4\pi }\left( \frac {1}{a} – \frac {1}{b}\right)　　　&（ハ）&　L\frac {\mathrm {d}I}{\mathrm {d}t} \\[ 5pt ] &（ニ）&　\frac {\mu _{0}I^{2}}{8\pi }\left( \frac {1}{a} – \frac {1}{b}\right)　　　&（ホ）&　\frac {\mu _{0}I^{2}}{4\pi }\ln {\frac {b}{a}}　　　&（ヘ）&　\frac {\mu _{0}I}{2\pi r} \\[ 5pt ] &（ト）&　\frac {\mu _{0}I}{4\pi r^{3}}　　　&（チ）&　\frac {\mu _{0}I}{8\pi }\left( \frac {1}{a^{2}} – \frac {1}{b^{2}}\right) 　　　&（リ）&　\frac {L^{2}I}{2} \\[ 5pt ] &（ヌ）&　\frac {\mu _{0}I}{2\pi }\ln {\frac {b}{a}} 　　　&（ル）&　\frac {LI^{2}}{2}　　　&（ヲ）&　\frac {\mu _{0}I^{2}}{16\pi }\left( \frac {1}{a^{2}} – \frac {1}{b^{2}}\right) 　 \\[ 5pt ] &（ワ）&　\frac {\mu _{0}I}{4\pi r^{2}}　　　&（カ）&　\frac {I^{2}}{L}　　　&（ヨ）&　LI
\end{eqnarray}
\]

【ワンポイント解説】

アンペールの周回積分の法則，インダクタンスの電磁気学と自然対数の積分の数学を使用します。電磁気は覚える公式が多いため大変ですが，問題に触れ少しずつ覚えていきましょう。本問では以下の公式を使用します。

1.アンペールの周回積分の法則
直線導体に電流$ \ I \ $を流した時，導体の周りに発生する磁界の大きさ$ \ H \ $との関係は，
\[
\begin{eqnarray}
I=\int_{c} \boldsymbol H \mathrm {d}\boldsymbol l \\[ 5pt ] \end{eqnarray}
\] となり，本問において導体から$ \ r \ $離れた箇所の磁界の大きさ$ \ H \ $との関係は，
\[
\begin{eqnarray}
I&=&2\pi r H　⇔　H&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.磁束密度$ \ B \ $と磁界の強さ$ \ H \ $の関係式
透磁率を$ \ \mu \ $とすると，磁束密度$ \ B \ $と磁界の強さ$ \ H \ $の関係は，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] \end{eqnarray}
\] となります。

3.自己インダクタンス$ \ L \ $と鎖交磁束数$ \ \mathit {\Phi} \ $の関係式
自己インダクタンス$ \ L \ $と鎖交磁束数$ \ \mathit {\Phi} \ $には，
\[
\begin{eqnarray}
LI&=&N\mathit {\Phi} (本問では巻数N=1) \\[ 5pt ] \end{eqnarray}
\] の関係があります。

4.自己インダクタンス$ \ L \ $と蓄積される電磁エネルギー$ \ W \ $の関係式
自己インダクタンス$ \ L \ $のコイルに電流$ \ I \ $を流し，十分時間が経った時にコイルに蓄積されるエネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W&=&\frac {LI^{2}}{2} \\[ 5pt ] \end{eqnarray}
\] となります。

5.自然対数の微分・積分
分数の積分は以下の通りとなります。電磁気では良く出てくる積分となるので，覚えておいて下さい。
\[
\begin{eqnarray}
\int ^{b}_{a}\frac {1}{x}\mathrm {d}x&=&\ln {b} -\ln {a}=\ln {\frac {b}{a}} \\[ 5pt ] \end{eqnarray}
\]

【関連する「電気の神髄」記事】

　　円筒導体の鎖交磁束とインダクタンス

【解答】

(1)解答：ヘ
内側導体及び外側導体に挟まれた領域すなわち$ \ a ＜ r ＜ b \ $では，貫く電流が内側導体を流れる電流$I$のみである。したがって，磁界の強さ$H_{\mathrm {r}}$はアンペールの周回積分の法則から，
\[
\begin{eqnarray}
H_{\mathrm {r}}&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] であり，磁束密度の大きさ$ \ B=\mu _{0}H_{\mathrm {r}} \ $の関係があるから，
\[
\begin{eqnarray}
B &=& \mu _{0}H_{\mathrm {r}} \\[ 5pt ] &=& \frac {\mu _{0}I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ヌ
題意より，鎖交磁束$ \ \mathit {\Phi} \ $は(1)の解答を用いて，
\[
\begin{eqnarray}
\mathit {\Phi} &=& \int ^{b}_{a}B\mathrm {d}r \\[ 5pt ] &=& \int ^{b}_{a}\frac {\mu _{0}I}{2\pi r}\mathrm {d}r \\[ 5pt ] &=& \frac {\mu _{0}I}{2\pi }\int ^{b}_{a}\frac {1}{r}\mathrm {d}r \\[ 5pt ] &=& \frac {\mu _{0}I}{2\pi }\left[ \ln {r}\right] ^{b}_{a} \\[ 5pt ] &=& \frac {\mu _{0}I}{2\pi }\left( \ln {b}-\ln {a}\right) \\[ 5pt ] &=& \frac {\mu _{0}I}{2\pi }\ln \frac {b}{a}
\end{eqnarray}
\] と求められる。

(3)解答：ヨ
ワンポイント解説の「3.自己インダクタンス$ \ L \ $と鎖交磁束数$ \ \mathit {\Phi} \ $の関係式」で述べた通り、解答は$ \ \displaystyle LI \ $となります。

(4)解答：ホ
題意より，単位長さ当たりに蓄積される磁気エネルギー$ \ W \ $は，
\[
\begin{eqnarray}
W &=& 2\pi \int ^{b}_{a} \frac {B^{2}}{2\mu _{0}} r\mathrm {d}r \\[ 5pt ] &=& 2\pi \int ^{b}_{a} \frac {\left[ \frac {\mu _{0}I}{2\pi r}\right] ^{2}}{2\mu _{0}} r\mathrm {d}r \\[ 5pt ] &=& \frac {\mu _{0}I^{2}}{4\pi }\int ^{b}_{a} \frac {1}{r}\mathrm {d}r \\[ 5pt ] &=& \frac {\mu _{0}I^{2}}{4\pi }\ln \frac {b}{a}
\end{eqnarray}
\] と求められる。

(5)解答：ル
ワンポイント解説の「4.自己インダクタンス$ \ L \ $と蓄積される電磁エネルギー$ \ W \ $の関係式」で述べた通り、解答は$ \ \displaystyle \frac {LI^{2}}{2} \ $となります。