《理論》〈電気回路〉[R07:問5]複数の電源及び抵抗から構成された回路の最大消費電力に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

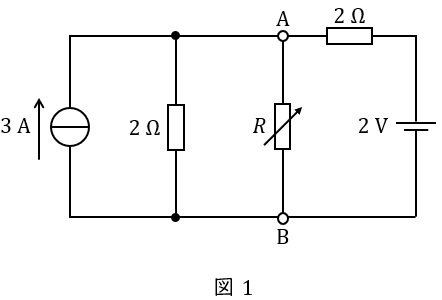
図1の直流回路は，直流電圧源，直流電流源及び抵抗から構成されており，端子$ \ \mathrm {A-B} \ $間の抵抗$ \ R \ $は可変抵抗である。以下の手順に従って，可変抵抗$ \ R \ $で消費される電力が最大となる条件及び最大消費電力を求める。

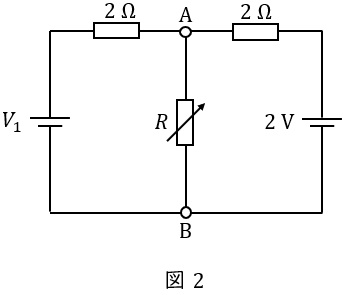
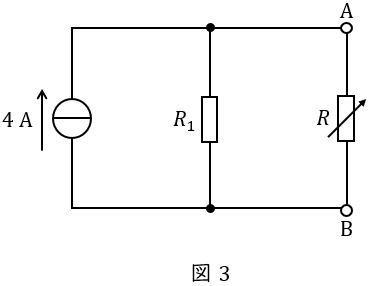
図1の回路を，二つの直流電圧源を用いた図2の等価回路に変換すると，図2の$ \ V_{1} \ $は$ \ \fbox {　（１）　} \ \mathrm {V} \ $となる。さらに，図2の回路を，一つの直流電流源を用いた図3の等価回路に変換すると，図3の$ \ R_{1} \ $は$ \ \fbox {　（２）　} \ \mathrm {\Omega } \ $となる。

図3の等価回路より，可変抵抗$ \ R \ $で消費される電力$ \ P \ $は，$ \ R \ $を用いて$ \ P= \ \fbox {　（３）　} \ \mathrm {[W]} \ $と表される。可変抵抗$ \ R \ $で消費される電力$ \ P \ $が最大となる条件は，$ \ R \ $を用いて$ \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}R}= \ \fbox {　（４）　} \ =0 \ $と表される。したがって，可変抵抗$ \ R \ $で消費される最大消費電力は$ \ \fbox {　（５）　} \ \mathrm {W} \ $となる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　1　　　　　&（ロ）&　2　　　　　&（ハ）&　3 \\[ 5pt ] &（ニ）&　4　　　　　&（ホ）&　5　　　　　&（ヘ）&　6 \\[ 5pt ] &（ト）&　8　　　　　&（チ）&　12　　　　　&（リ）&　16 \\[ 5pt ] &（ヌ）&　-\frac {16\left( R-1\right) }{\left( R+1\right) ^{3}}　　　　　&（ル）&　\frac {16\left( R-2\right) }{\left( R+2\right) ^{4}} 　　　　&（ヲ）&　\frac {16R }{\left( R+1\right) ^{2}} \\[ 5pt ] &（ワ）&　\frac {16\left( R-1\right) }{\left( R+1\right) ^{3}}　　　　　&（カ）&　\frac {4R }{\left( R+2\right) ^{2}}　　　　　&（ヨ）&　\frac {16R }{R+1} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

回路変形を用いた直流回路の最大消費電力を求める問題です。
ノートンの定理を使用したり商の微分を計算させたりする等，直流回路の難易度としては例年と比較しても高い問題であったかと思います。
焦るとミスが発生するので，まずは落ち着いて(1)だけは間違えないように注意しましょう。

1.テブナンの定理
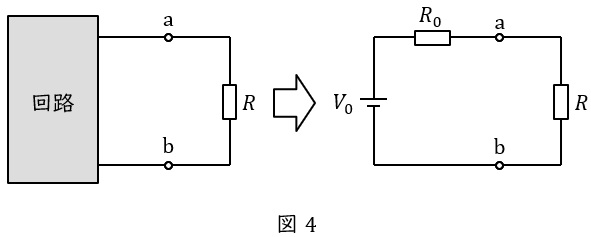
図4のように複雑な回路を電圧源$ \ V_{0} \ \mathrm {[V]} \ $と抵抗$ \ R_{0} \ \mathrm {[\Omega ]} \ $に置き換える方法です。
$ \ V_{0} \ \mathrm {[V]} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $の開放電圧，$ \ R_{0} \ \mathrm {[\Omega ]} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $から電源側回路を見た合成抵抗となります。
ただし，$ \ R_{0} \ \mathrm {[\Omega ]} \ $を求める際，電圧源は短絡，電流源は開放します。

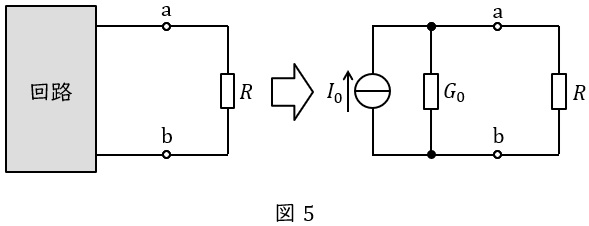
2.ノートンの定理
図5のように複雑な回路を電流源$ \ I_{0} \ \mathrm {[A]} \ $とコンダクタンス$ \ G_{0} \ \mathrm {[S]} \ $（抵抗の逆数）に置き換える方法です。
$ \ I_{0} \ \mathrm {[A]} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $を短絡したときの短絡電流，$ \ G_{0} \ \mathrm {[S]} \ $は端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $から電源側回路を見た合成コンダクタンスとなります。
ただし，$ \ G_{0} \ \mathrm {[S]} \ $を求める際，電圧源は短絡，電流源は開放します。

3.電圧源と電流源の等価変換
図6に示すように，電圧源と電流源は抵抗との直列接続と並列接続で等価変換をすることができます。
電圧源の電圧$ \ E \ \mathrm {[V]} \ $と電流源の電流$ \ I \ \mathrm {[A]} \ $には，
\[
\begin{eqnarray}
E &=&rI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

4.積と商の微分公式（数学）
$ \ x \ $の関数$ \ u\left( x \right) \ $及び$ \ v\left( x \right) \ $があり，それぞれの微分が$ \ u^{\prime }\left( x \right) \ $及び$ \ v^{\prime }\left( x \right) \ $であるとき，それぞれの積と商の微分は，
\[
\begin{eqnarray}
\left\{ u\left( x \right) v\left( x \right) \right\} ^{\prime }&=&u^{\prime }\left( x \right) v\left( x \right) +u\left( x \right) v^{\prime }\left( x \right) \\[ 5pt ] \left\{ \frac {u\left( x \right) }{v\left( x \right) }\right\} ^{\prime }&=&\frac {u^{\prime }\left( x \right) v\left( x \right) -u\left( x \right) v^{\prime }\left( x \right) }{v\left( x \right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヘ
図1の$ \ 3 \ \mathrm {A} \ $の電流源と$ \ 2 \ \mathrm {\Omega } \ $の抵抗を等価変換すると図2の$ \ V_{1} \ \mathrm {[V]} \ $は，ワンポイント解説「3.電圧源と電流源の等価変換」の通り，
\[
\begin{eqnarray}
V_{1} &=&3\times 2 \\[ 5pt ] &=&6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：イ
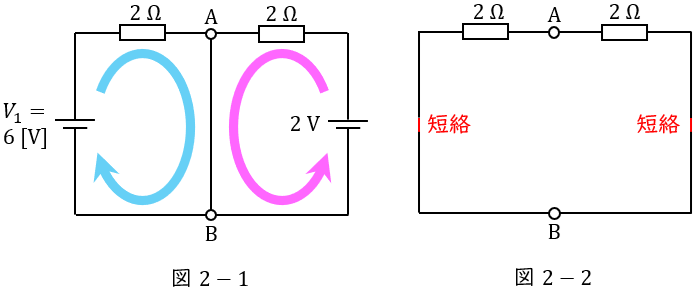
ワンポイント解説「2.ノートンの定理」の通り，図2の回路にノートンの定理を適用すると，$ \ R \ \mathrm {[\Omega ]} \ $を短絡したときの短絡電流$ \ I_{0} \ \mathrm {[A]} \ $は，図2-1の通り各電源から短絡点に電流が流れると考えれば良いので，
\[
\begin{eqnarray}
I_{0} &=&\frac {V_{1}}{2}+\frac {2}{2} \\[ 5pt ] &=&\frac {6}{2}+\frac {2}{2} \\[ 5pt ] &=&4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，端子$ \ \mathrm {a} \ – \ \mathrm {b} \ $から電源側回路を見た合成コンダクタンス$ \ \displaystyle \frac {1}{R_{1}} \ \mathrm {[S]} \ $を求める式より$ \ R_{1} \ \mathrm {[\Omega ]} \ $は，図2-2の通り，
\[
\begin{eqnarray}
\frac {1}{R_{1}} &=&\frac {1}{2}+\frac {1}{2} \\[ 5pt ] &=&1 \\[ 5pt ] R_{1}&=&1 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヲ
図3の回路において，可変抵抗$ \ R \ \mathrm {[\Omega ]} \ $に流れる電流$ \ I_{\mathrm {AB}} \ \mathrm {[A]} \ $は，分流の法則より，
\[
\begin{eqnarray}
I_{\mathrm {AB}} &=&\frac {R_{1}}{R+R_{1}}I_{0} \\[ 5pt ] &=&\frac {1}{R+1}\times 4 \\[ 5pt ] &=&\frac {4}{R+1} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，$ \ R \ \mathrm {[\Omega ]} \ $で消費される電力$ \ P \ \mathrm {[W]} \ $は，
\[
\begin{eqnarray}
P &=&R{I_{\mathrm {AB}}}^{2} \\[ 5pt ] &=&R\left( \frac {4}{R+1}\right) ^{2} \\[ 5pt ] &=&\frac {16R }{\left( R+1\right) ^{2}} \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヌ
$ \ u\left( R\right) =16R \ $，$ \ v\left( R\right) =\left( R+1\right) ^{2} \ $とおき，さらに$ \ t=R+1 \ $とおくと，$ \ v\left( t\right) =t ^{2} \ $となり，それぞれの微分$ \ u^{\prime }\left( R\right) \ $と$ \ v^{\prime }\left( R\right) \ $は，
\[
\begin{eqnarray}
u^{\prime }\left( R\right) &=&16 \\[ 5pt ] v^{\prime }\left( R\right) &=&\frac {\mathrm {d}v}{\mathrm {d}t}\cdot \frac {\mathrm {d}t}{\mathrm {d}R} \\[ 5pt ] &=&2t\cdot 1 \\[ 5pt ] &=&2\left( R+1\right) \\[ 5pt ] \end{eqnarray}
\] となるから，$ \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}R} \ $は，ワンポイント解説「4.積と商の微分公式」の通り，
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}R} &=&\frac {u^{\prime }\left( R \right) v\left( R \right) -u\left( R \right) v^{\prime }\left( R \right) }{v\left( R \right) ^{2}} \\[ 5pt ] &=&\frac {16\times \left( R+1\right) ^{2} -16R \times 2\left( R+1\right) }{\left( R+1\right) ^{4}} \\[ 5pt ] &=&\frac {16 \left( R+1\right) -16R \times 2 }{\left( R+1\right) ^{3}} \\[ 5pt ] &=&\frac {16R+16 -32R }{\left( R+1\right) ^{3}} \\[ 5pt ] &=&\frac {-16R+16 }{\left( R+1\right) ^{3}} \\[ 5pt ] &=&-\frac {16\left( R-1\right) }{\left( R+1\right) ^{3}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
(4)解答式より，$ \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}R}=0 \ $のとき，
\[
\begin{eqnarray}
-\frac {16\left( R-1\right) }{\left( R+1\right) ^{3}} &=&0 \\[ 5pt ] R-1&=&0 \\[ 5pt ] R&=&1 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，これを(3)解答式に代入すると，$ \ R \ $で消費される最大消費電力は$ \ P_{\mathrm {m}} \ \mathrm {[W]} \ $は，
\[
\begin{eqnarray}
P_{\mathrm {m}} &=&\frac {16R }{\left( R+1\right) ^{2}} \\[ 5pt ] &=&\frac {16\times 1 }{\left( 1+1\right) ^{2}} \\[ 5pt ] &=&4 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。