《理論》〈電気回路〉[H28:問3] 回路の過渡現象に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】
- 3.1 【本問に関する質疑応答】

【問題】

【難易度】★★★★★（難しい）

次の文章は，回路の過渡現象に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

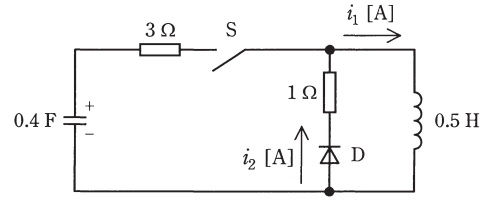
図のような$ \ RLC \ $回路を考える。なお，$ \ \mathrm {D} \ $は順方向にのみ電流を流し，そのときの電圧降下が零であるような特性をもつ理想的なダイオードとする。初期状態ではスイッチ$ \ \mathrm {S} \ $は開いており，コイルには電流が流れておらず，コンデンサは$ \ 1 \ \mathrm {V} \ $に充電されている。時刻$ \ t=0 \ $でスイッチを閉じると，直後にはダイオード$ \ \mathrm {D} \ $には逆向きの電圧が印加されるため，電流$ \ i_{2}=0 \ $となる。$ \ i_{2}=0 \ $である場合の電流$ \ i_{1} ( t ) \ $は，
初期条件
\[
\begin{eqnarray}
i_{1} ( 0 ) &=&0 \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
{\mathrm {d}i_{1} ( t ) \abovewithdelims . | 0.5pt \mathrm {d}t}_{t=0} &=&\fbox {　（１）　} \\[ 5pt ] \end{eqnarray}
\] を用いて，
\[
\begin{eqnarray}
i_{1} ( t ) &=&\fbox {　（２）　} \ \mathrm {e}^{-t}+\fbox {　（３）　} \ \mathrm {e}^{- \ \fbox {　（４）　} \ t} \\[ 5pt ] \end{eqnarray}
\] と表される。
ダイオード$ \ \mathrm {D} \ $には，印加される電圧が反転する時刻以降電流が流れる。ダイオード$ \ \mathrm {D} \ $に印加される電圧が反転する時刻は，コイルの両端電圧$ \ \displaystyle L\frac {\mathrm {d}i_{1} ( t ) }{\mathrm {d}t} \ $が反転する時刻に一致することを利用すると，スイッチ$ \ \mathrm {S} \ $を投入してからダイオード$ \ \mathrm {D} \ $に電流が流れ始めるまでの時間は$ \ \fbox {　（５）　} \ \mathrm {s} \ $と求められる。
なお，$ \ \ln 5≒1.6 \ $としてよい。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　-2　　　&（ロ）&　-1　　　&（ハ）&　-0.5 \\[ 5pt ] &（ニ）&　0.2　　　&（ホ）&　0.25　　　&（ヘ）&　0.4 \\[ 5pt ] &（ト）&　0.5　　　&（チ）&　0.8 　　　&（リ）&　1 \\[ 5pt ] &（ヌ）&　1.5 　　　&（ル）&　2　　　&（ヲ）&　2.5　 \\[ 5pt ] &（ワ）&　4　　　&（カ）&　5　　　&（ヨ）&　10
\end{eqnarray}
\]

【ワンポイント解説】

本問はあまり出題されない二階微分の方程式を解く必要があります。二種としては非常に高度な計算が要求され，選択肢も絞ることができないので，本問が解けるかどうかで合否を大きくわけることとなりそうです。

1.過渡現象における$ \ RLC \ $それぞれの電圧
線路に流れる電流を$ \ i \ $とし，抵抗$ \ R \ $の電圧$ \ V_{\mathrm{R}} \ $，リアクトル$ \ L \ $の電圧$ \ V_{\mathrm{L}} \ $，コンデンサ$ \ C \ $の電圧$ \ V_{\mathrm{C}} \ $とすると，
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] となり，電荷$ \ q \ $との間に$ \ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ $の関係があるので，
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& R\frac {\mathrm {d}q}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {q}{C}
\end{eqnarray}
\] となります。

【解答】

(1)解答：ル
時刻$ \ t=0 \ $でスイッチを閉じた直後回路に電流は流れず，抵抗での電圧降下はないので，コンデンサに充電されている$ \ 1 \ \mathrm {V} \ $はすべてリアクトルにかかる。よって，
\[
\begin{eqnarray}
L {\mathrm {d}i_{1} ( t ) \abovewithdelims . | 0.5pt \mathrm {d}t}_{t=0} &=&1 \\[ 5pt ] \end{eqnarray}
\] で$ \ L=0.5 \ \mathrm {H} \ $であるから，
\[
\begin{eqnarray}
{\mathrm {d}i_{1} ( t ) \abovewithdelims . | 0.5pt \mathrm {d}t}_{t=0} &=&2 \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ト
(3)解答：ハ
(4)解答：カ
スイッチ投入後の回路方程式は，ダイオードに電流が流れないので，
\[
\begin{eqnarray}
L\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}}+R\frac {\mathrm {d}q}{\mathrm {d}t}+\frac {q}{C}&=&0 \\[ 5pt ] 0.5\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}}+3\frac {\mathrm {d}q}{\mathrm {d}t}+\frac {q}{0.4}&=&0 \\[ 5pt ] \frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}}+6\frac {\mathrm {d}q}{\mathrm {d}t}+5q&=&0 \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$ \ \displaystyle q=C\mathrm {e}^{Pt} \ $ ( $ \ C \ $，$ \ P \ $は定数 )とおくと，
\[
\begin{eqnarray}
\frac {\mathrm {d}q}{\mathrm {d}t} &=& PC\mathrm {e}^{Pt}\\[ 5pt ] \frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}} &=& P^{2}C\mathrm {e}^{Pt} \\[ 5pt ] \end{eqnarray}
\] となるので，これを回路方程式に代入し解くと，
\[
\begin{eqnarray}
P^{2}C\mathrm {e}^{Pt}+6PC\mathrm {e}^{Pt}+5C\mathrm {e}^{Pt}&=&0 \\[ 5pt ] P^{2}+6P+5&=&0 \\[ 5pt ] \left( P +1 \right) \left( P +5\right) &=&0 \\[ 5pt ] P&=&-1，-5 \\[ 5pt ] \end{eqnarray}
\] となり，$ \ q \ $の一般解は，$ \ q=C_{1}\mathrm {e}^{-t}+C_{2}\mathrm {e}^{-5t} \ $( $ \ C_{1} \ $，$ \ C_{2} \ $は定数 )となる。よって，$ \ i \ $の一般解は，
\[
\begin{eqnarray}
i_{1}&=&\frac {\mathrm {d}q}{\mathrm {d}t}&=&C_{1}^{\prime}\mathrm {e}^{-t}+C_{2}^{\prime}\mathrm {e}^{-5t} \\[ 5pt ] \end{eqnarray}
\] となる。初期条件より，
\[
\begin{eqnarray}
i_{1} ( 0 ) &=&　C_{1}^{\prime}&+&C_{2}^{\prime}&=&0 \\[ 5pt ] {\mathrm {d}i_{1} ( t ) \abovewithdelims . | 0.5pt \mathrm {d}t}_{t=0} &=&-C_{1}^{\prime}&-&5C_{2}^{\prime}&=&2 \\[ 5pt ] \end{eqnarray}
\] であるから，この連立方程式を解くと，
\[
\begin{eqnarray}
C_{1}^{\prime}&=&0.5，C_{2}^{\prime}&=&-0.5 \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，求める電流は，
\[
\begin{eqnarray}
i_{1} ( t ) &=&0.5\mathrm {e}^{-t}-0.5\mathrm {e}^{-5t} \\[ 5pt ] \end{eqnarray}
\] となる。

(5)解答：ヘ
ダイオードに電流が流れ始めるのは，リアクトルにかかる電圧が負となった瞬間であるから，リアクトルにかかる電圧$ \ \displaystyle L\frac {\mathrm {d}i_{1}}{\mathrm {d}t} \ $が零となる時間を求めればよい。よって，
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{1}}{\mathrm {d}t}&=&0 \\[ 5pt ] 0.5\times \left( -0.5\mathrm {e}^{-t}+2.5\mathrm {e}^{-5t}\right) &=&0 \\[ 5pt ] \mathrm {e}^{-t}&=& 5\mathrm {e}^{-5t}\\[ 5pt ] \mathrm {e}^{4t}&=&5 \\[ 5pt ] 4t&=&\ln 5 \\[ 5pt ] 4t&=&1.6 \\[ 5pt ] t&=&0.4 \\[ 5pt ] \end{eqnarray}
\] と求められる。