【問題】
【難易度】★★★☆☆(普通)
次の文章は,平行平板コンデンサに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
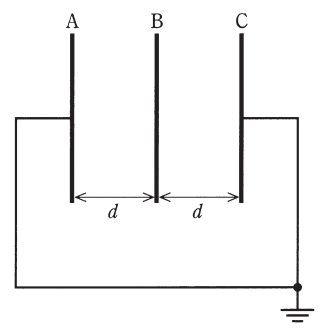
図のように,誘電率\( \ \varepsilon _{\mathrm {0}} \ \)の空間に\( \ 3 \ \)枚の極板\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)が,互いに平行に置かれており,極板\( \ \mathrm {A} \ \)と\( \ \mathrm {C} \ \)は導線で接続され,接地されている。極板の面積はすべて\( \ S \ \)であり,\( \ \mathrm {A}-\mathrm {B} \ \)間,\( \ \mathrm {B}-\mathrm {C} \ \)間の距離は\( \ d \ \)である。極板端部の影響は無視するものとする。
極板\( \ \mathrm {B} \ \)に電荷\( \ 2Q \ \)を与える。このとき,極板\( \ \mathrm {A}-\mathrm {B} \ \)間と\( \ \mathrm {B}-\mathrm {C} \ \)間の電界は等しく\( \ \fbox { (1) } \ \)であり,それぞれの静電容量も等しく\( \ \fbox { (2) } \ \)である。次に,極板\( \ \mathrm {B} \ \)を\( \ \mathrm {C} \ \)側に\( \ x \left( x<d\right) \ \)だけ平行移動させた状態を考える。このとき,極板\( \ \mathrm {B} \ \)の\( \ \mathrm {A} \ \)側の電荷を\( \ Q_{1} \ \),\( \ \mathrm {C} \ \)側の電荷を\( \ Q_{2} \ \)とすると,電荷保存則より\( \ \fbox { (3) } \ \)が成り立つから,極板\( \ \mathrm {B} \ \)の電位は\( \ \fbox { (4) } \ \)となる。極板\( \ \mathrm {B} \ \)を移動する前の極板間のエネルギーの和を\( \ W \ \),移動後のエネルギーの和を\( \ W^{\prime } \ \)とすると,両者の関係は\( \ \fbox { (5) } \ \)である。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& W>W^{\prime } &(ロ)& Q_{1}+Q_{2}=2Q &(ハ)& \frac {Qd}{\varepsilon _{0}S}\left( d-x\right) \\[ 5pt ]
&(ニ)& Q_{1}+Q_{2}=Q &(ホ)& \frac {Q}{\varepsilon _{0}S} &(ヘ)& \frac {\varepsilon _{0}d}{S} \\[ 5pt ]
&(ト)& \frac {\varepsilon _{0}Q}{S} &(チ)& \frac {S}{\varepsilon _{0}d} &(リ)& \frac {\varepsilon _{0}Qd}{S}\left( 1-\frac {x^{2}}{d^{2}}\right) \\[ 5pt ]
&(ヌ)& \frac {Qd}{\varepsilon _{0}S}\left( 1-\frac {x^{2}}{d^{2}}\right) &(ル)& W=W^{\prime } &(ヲ)& \frac {\varepsilon _{0}S}{d} \\[ 5pt ]
&(ワ)& \frac {S}{\varepsilon _{0}Q} &(カ)& W<W^{\prime } &(ヨ)& Q_{1}=Q_{2} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
総じて難易度が高い平成24年度の理論ですが,本問に関しては比較的標準レベルの問題であると言えます。平行平板コンデンサはかなりの頻度で出題されているので,基本をよく理解して,確実に得点できるようにしておきましょう。
1.平行平板コンデンサの極板間に現れる電荷\( \ Q \ \)
静電容量\( \ C \ \)のコンデンサに電圧\( \ V \ \)をかけ十分に時間が経った時に各極板に現れる電荷\( \ Q \ \)は,
\[
\begin{eqnarray}
Q&=&CV \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.平行平板コンデンサの静電容量\( \ C \ \)
極板間の誘電率\( \ \varepsilon \ \),各極板の面積\( \ S \ \),極板間の距離\( \ d \ \)とすると,このコンデンサの静電容量\( \ C \ \)は,
\[
\begin{eqnarray}
C&=&\frac {\varepsilon S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.平行平板コンデンサ内の電界\( \ E \ \)
極板間の距離\( \ d \ \)の平行平板コンデンサに電圧\( \ V \ \)をかけた時,平行平板コンデンサ内の電界\( \ E \ \)は,
\[
\begin{eqnarray}
E &=&\frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.コンデンサの静電エネルギー\( \ W \ \)
静電容量\( \ C \ \)のコンデンサに電圧\( \ V \ \)をかけた時にコンデンサに蓄えられる静電エネルギー\( \ W \ \)は,
\[
\begin{eqnarray}
W&=&\frac {1}{2}CV^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,「1.平行平板コンデンサの極板間に現れる電荷\( \ Q \ \)」の関係式を用いると,
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ]
&=&\frac {Q^{2}}{2C} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ホ
(2)解答:ヲ
極板の面積はすべて\( \ S \ \)であり,\( \ \mathrm {A}-\mathrm {B} \ \)間,\( \ \mathrm {B}-\mathrm {C} \ \)間の距離は\( \ d \ \)なので,その静電容量\( \ C \ \)は,ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」より,
\[
\begin{eqnarray}
C&=&\frac {\varepsilon_{0} S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となる。極板\( \ \mathrm {B} \ \)に電荷\( \ 2Q \ \)を与えると,極板\( \ \mathrm {A}-\mathrm {B} \ \)間と\( \ \mathrm {B}-\mathrm {C} \ \)間にはそれぞれ電荷\( \ Q \ \)が分担されるので,極板\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \)は,ワンポイント解説「1.平行平板コンデンサの極板間に現れる電荷\( \ Q \ \)」より,
\[
\begin{eqnarray}
Q&=&CV_{\mathrm {B}} \\[ 5pt ]
V_{\mathrm {B}}&=&\frac {Q}{C} \\[ 5pt ]
&=&\frac {Q}{\displaystyle \frac {\varepsilon_{0} S}{d}} \\[ 5pt ]
&=&\frac {Qd}{\varepsilon_{0} S} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,極板\( \ \mathrm {A}-\mathrm {B} \ \)間と\( \ \mathrm {B}-\mathrm {C} \ \)間の電界\( \ E \ \)は,ワンポイント解説「3.平行平板コンデンサ内の電界\( \ E \ \)」より,
\[
\begin{eqnarray}
E &=&\frac {V_{\mathrm {B}}}{d} \\[ 5pt ]
&=&\frac {\displaystyle \frac {Qd}{\varepsilon_{0} S}}{d} \\[ 5pt ]
&=&\frac {Q}{\varepsilon _{0}S} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ロ
極板\( \ \mathrm {B} \ \)は絶縁されているので,電荷は保存され\( \ Q_{1}+Q_{2}=2Q \ \)が成立する。
(4)解答:ヌ
極板\( \ \mathrm {B} \ \)が\( \ x \ \)移動したときの\( \ \mathrm {A}-\mathrm {B} \ \)間,\( \ \mathrm {B}-\mathrm {C} \ \)間の静電容量\( \ C_{\mathrm {AB}} \ \)及び\( \ C_{\mathrm {BC}} \ \)は,ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」より,
\[
\begin{eqnarray}
C_{\mathrm {AB}}&=&\frac {\varepsilon_{0} S}{d+x} \\[ 5pt ]
C_{\mathrm {BC}}&=&\frac {\varepsilon_{0} S}{d-x} \\[ 5pt ]
\end{eqnarray}
\]
となるので,それぞれ蓄えられる電荷\( \ Q_{1} \ \)及び\( \ Q_{2} \ \)は,
\[
\begin{eqnarray}
Q_{1}&=&C_{\mathrm {AB}}V_{\mathrm {B}} \\[ 5pt ]
&=&\frac {\varepsilon_{0} SV_{\mathrm {B}}}{d+x} \\[ 5pt ]
Q_{2}&=&C_{\mathrm {BC}}V_{\mathrm {B}} \\[ 5pt ]
&=&\frac {\varepsilon_{0} SV_{\mathrm {B}}}{d-x} \\[ 5pt ]
\end{eqnarray}
\]
となり,(3)より\( \ Q_{1}+Q_{2}=2Q \ \)が成り立つから,
\[
\begin{eqnarray}
2Q&=&Q_{1}+Q_{2} \\[ 5pt ]
&=&\frac {\varepsilon_{0} SV_{\mathrm {B}}}{d+x}+\frac {\varepsilon_{0} SV_{\mathrm {B}}}{d-x} \\[ 5pt ]
&=&\varepsilon_{0} SV_{\mathrm {B}}\left( \frac {1}{d+x}+\frac {1}{d-x}\right) \\[ 5pt ]
&=&\varepsilon_{0} SV_{\mathrm {B}}\cdot \frac {\left( d-x\right) +\left( d+x\right) }{\left( d+x\right) \left( d-x\right)} \\[ 5pt ]
&=&\varepsilon_{0} SV_{\mathrm {B}}\cdot \frac {2d}{d^{2}-x^{2}} \\[ 5pt ]
&=&\frac {2\varepsilon_{0} SdV_{\mathrm {B}}}{d^{2}-x^{2}} \\[ 5pt ]
V_{\mathrm {B}}&=&2Q\cdot \frac {d^{2}-x^{2}}{2\varepsilon_{0} Sd} \\[ 5pt ]
&=&\frac {Q}{\varepsilon_{0} S}\cdot \frac {d^{2}-x^{2}}{d} \\[ 5pt ]
&=&\frac {Qd}{\varepsilon_{0} S}\cdot \frac {d^{2}-x^{2}}{d^{2}} \\[ 5pt ]
&=&\frac {Qd}{\varepsilon _{0}S}\left( 1-\frac {x^{2}}{d^{2}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:イ
極板\( \ \mathrm {B} \ \)を移動する前の極板間のエネルギーの和\( \ W \ \)は,ワンポイント解説「4.コンデンサの静電エネルギー\( \ W \ \)」より,
\[
\begin{eqnarray}
W&=&\frac {Q^{2}}{2C}+\frac {Q^{2}}{2C} \\[ 5pt ]
&=&\frac {Q^{2}}{C} \\[ 5pt ]
&=&\frac {Q^{2}}{\displaystyle \frac {\varepsilon_{0} S}{d}} \\[ 5pt ]
&=&\frac {Q^{2}d}{\varepsilon_{0} S} \\[ 5pt ]
\end{eqnarray}
\]
であり,移動後のエネルギーの和\( \ W^{\prime } \ \)は,ワンポイント解説「4.コンデンサの静電エネルギー\( \ W \ \)」より,
\[
\begin{eqnarray}
W^{\prime }&=&\frac {1}{2}C_{\mathrm {AB}}V_{\mathrm {B}}^{2}+\frac {1}{2}C_{\mathrm {BC}}V_{\mathrm {B}}^{2} \\[ 5pt ]
&=&\frac {1}{2}\cdot \frac {\varepsilon_{0} S}{d+x}\left( \frac {Q}{\varepsilon_{0} S}\cdot \frac {d^{2}-x^{2}}{d}\right)^{2}+\frac {1}{2}\cdot \frac {\varepsilon_{0} S}{d-x}\left( \frac {Q}{\varepsilon_{0} S}\cdot \frac {d^{2}-x^{2}}{d}\right)^{2} \\[ 5pt ]
&=&\frac {\varepsilon_{0} S}{2}\left( \frac {Q}{\varepsilon_{0} S}\cdot \frac {d^{2}-x^{2}}{d}\right)^{2}\left( \frac {1}{d+x} + \frac {1}{d-x}\right) \\[ 5pt ]
&=&\frac {\varepsilon_{0} S}{2}\left( \frac {Q}{\varepsilon_{0} S}\cdot \frac {d^{2}-x^{2}}{d}\right)^{2}\cdot \frac {2d}{d^{2}-x^{2}} \\[ 5pt ]
&=&\frac {Q^{2}}{\varepsilon_{0} S}\cdot \frac {d^{2}-x^{2}}{d} \\[ 5pt ]
&=&\frac {Q^{2}d}{\varepsilon_{0} S}\left( 1-\frac {x^{2}}{d^{2}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ x>0 \ \)及び\( \ d>0 \ \)であることから\( \ W>W^{\prime } \ \)が求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは