【問題】
【難易度】★★★☆☆(普通)
送電線の抵抗とリアクタンスの求め方に関して,次の問に答えよ。
送電線両端の電圧や位相角が測定できると,送電線の抵抗やリアクタンスが求められる。送電端電圧\({\dot V}_{1}\)の大きさを\(V_{1}\),その受電端電圧\({\dot V}_{2}\)に対する位相差を\(\delta \),送電端から受電端への潮流の送電端側の有効電力を\(P\),無効電力を\(Q\)とする。また,送電線の並列アドミタンスは無視できるものとし,送電端の抵抗を\(r\),リアクタンスを\(x\)とする。
ただし,電力や電流は送電端から受電端への向きを正,無効電力は遅れ側を正,及び\(P≠0\)あるいは\(Q≠0\)とする。また,\(\delta \)の単位は\(\mathrm {[rad]}\),その他の単位は\(\mathrm {[p.u.]}\)とする。
(1) 送電端と受電端の複素電圧をそれぞれ\({\dot V}_{1}=V_{1} \angle \delta\),\({\dot V}_{2}=V_{2} \angle 0\),送電線電流を\(\dot I\)としたとき,\({\dot V}_{1}\)を\({\dot V}_{2}\),\(\dot I\),\(r\),\(x\)を用いて表せ。
(2) \(\dot I\)を,\(P\),\(Q\),\({\dot V}_{1}\)を用いて表せ。
(3) 上記(1)及び(2)にて表した式から\(\dot I\)を消去して\(V_{1}\),\(V_{2}\),\(\delta \),\(P\),\(Q\),\(r\),\(x\)間の関係を表す式を示せ。
(4) 上記(3)の式で,実数部と虚数部に分けて考えると,\(x\)と\(r\)に関する下記の式が導かれる。\(\alpha \)と\(\beta \)は,\(V_{1}\),\(V_{2}\),\(\delta \)の関数である。\(\alpha \)と\(\beta \)を表す式を示せ。
\[
x=\frac {P\alpha +Q\beta }{P^{2}+Q^{2}}, r=\frac {P\beta -Q\alpha }{P^{2}+Q^{2}}
\]
(5) \(V_{1}=1.05 \ \mathrm {p.u.}\),\(V_{2}=1.01 \ \mathrm {p.u.}\),\(\displaystyle \delta =\frac {\pi}{12} \ \mathrm {rad}\),\(P=1.23 \ \mathrm {p.u.}\),\(Q=0.195 \ \mathrm {p.u.}\)のときの\(x \ \mathrm {[p.u.]}\)と\(r \ \mathrm {[p.u.]}\)を求めよ。
なお,\(\displaystyle \sin \frac {\pi}{12}=0.25882\),\(\displaystyle \cos \frac {\pi}{12}=0.96593\)を使用すること。
【ワンポイント解説】
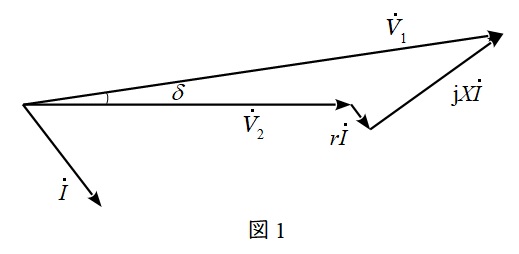
送電線の送電電力や無効電力の計算の導出方法に関する問題で,ベクトル図を描いてよく考えることが必要です。\(\delta ≒0(\sin \delta ≒0)\)の時の送電電力が一次試験で暗記したことがある式に一致することも合わせて確認しておくと理解が深まると思います。
【解答】
(1)\({\dot V}_{1}\)を\({\dot V}_{2}\),\(\dot I\),\(r\),\(x\)を用いて表す
図1のベクトル図より,
\[
\begin{eqnarray}
{\dot V}_{1}&=& {\dot V}_{2}+r\dot I+\mathrm {j}x\dot I \\[ 5pt ]
&=& {\dot V}_{2}+\left( r+\mathrm {j}x\right) \dot I \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\(\dot I\)を,\(P\),\(Q\),\({\dot V}_{1}\)を用いて表す
遅れ無効電力を正とすると,送電端側の電力は,
\[
P+\mathrm {j}Q={\dot V}_{1}\overline {\dot I}
\]
となるので,
\[
\begin{eqnarray}
\overline {\dot I}&=& \frac {P+\mathrm {j}Q}{{\dot V}_{1}} \\[ 5pt ]
\dot I&=& \frac {\overline {P+\mathrm {j}Q}}{\overline {{\dot V}_{1}}} \\[ 5pt ]
&=& \frac {P-\mathrm {j}Q}{\overline {{\dot V}_{1}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\(V_{1}\),\(V_{2}\),\(\delta \),\(P\),\(Q\),\(r\),\(x\)間の関係を表す式
(1),(2)より,\(\dot I\)を消去すると,
\[
\begin{eqnarray}
{\dot V}_{1}&=& {\dot V}_{2}+\left( r+\mathrm {j}x\right) \frac {P-\mathrm {j}Q}{\overline {{\dot V}_{1}}} \\[ 5pt ]
{\dot V}_{1}\overline {{\dot V}_{1}}&=& \overline {{\dot V}_{1}}{\dot V}_{2}+\left( r+\mathrm {j}x\right) \left( P-\mathrm {j}Q\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\({\dot V}_{1}=V_{1}\left( \cos \delta +\mathrm {j}\sin \delta \right) \),\({\dot V}_{2}=V_{2}\)となるので,
\[
\begin{eqnarray}
V_{1}\left( \cos \delta +\mathrm {j}\sin \delta \right) V_{1}\left( \cos \delta -\mathrm {j}\sin \delta \right) &=& V_{1}\left( \cos \delta -\mathrm {j}\sin \delta \right) V_{2}+\left( r+\mathrm {j}x\right) \left( P-\mathrm {j}Q\right) \\[ 5pt ]
V_{1}^{2}\left( \cos ^{2}\delta +\sin ^{2}\delta \right) &=& V_{1}V_{2}\left( \cos \delta -\mathrm {j}\sin \delta \right) +\left( r+\mathrm {j}x\right) \left( P-\mathrm {j}Q\right) \\[ 5pt ]
V_{1}^{2} &=& V_{1}V_{2}\left( \cos \delta -\mathrm {j}\sin \delta \right) +\left( r+\mathrm {j}x\right) \left( P-\mathrm {j}Q\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\(\alpha \)と\(\beta \)を表す式
(3)の解答式について,左辺右辺とも整理すると,
\[
\begin{eqnarray}
V_{1}^{2} &=& V_{1}V_{2}\left( \cos \delta -\mathrm {j}\sin \delta \right) +\left( r+\mathrm {j}x\right) \left( P-\mathrm {j}Q\right) \\[ 5pt ]
V_{1}^{2}-V_{1}V_{2}\left( \cos \delta -\mathrm {j}\sin \delta \right) &=& \left( r+\mathrm {j}x\right) \left( P-\mathrm {j}Q\right) \\[ 5pt ]
V_{1}^{2}-V_{1}V_{2}\cos \delta +\mathrm {j}V_{1}V_{2}\sin \delta &=& Pr+Qx +\mathrm {j} \left( -Qr+Px \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,実数部と虚数部を比較すると,
\[
\begin{eqnarray}
V_{1}^{2}-V_{1}V_{2}\cos \delta &=& Pr+Qx & ・・・・・ ①&\\[ 5pt ]
V_{1}V_{2}\sin \delta &=& -Qr+Px & ・・・・・ ②&\\[ 5pt ]
\end{eqnarray}
\]
となる。\(①\times Q +②\times P\)により\(r\)を消去すると,
\[
\begin{eqnarray}
PV_{1}V_{2}\sin \delta +Q\left( V_{1}^{2}-V_{1}V_{2}\cos \delta \right) &=& \left( P^{2}+Q^{2}\right) x \\[ 5pt ]
x &=& \frac {PV_{1}V_{2}\sin \delta +Q\left( V_{1}^{2}-V_{1}V_{2}\cos \delta \right) }{ P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。\(①\times P -②\times Q\)により\(x\)を消去すると,
\[
\begin{eqnarray}
P\left( V_{1}^{2}-V_{1}V_{2}\cos \delta \right) -QV_{1}V_{2}\sin \delta &=& \left( P^{2}+Q^{2}\right) r \\[ 5pt ]
r &=& \frac {P\left( V_{1}^{2}-V_{1}V_{2}\cos \delta \right) -QV_{1}V_{2}\sin \delta }{ P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって\(\alpha \)と\(\beta \)は,
\[
\begin{eqnarray}
\alpha &=& V_{1}V_{2}\sin \delta \\[ 5pt ]
\beta &=& V_{1}^{2}-V_{1}V_{2}\cos \delta \\[ 5pt ]
\end{eqnarray}
\]
となる。
(5)\(V_{1}=1.05 \ \mathrm {p.u.}\),\(V_{2}=1.01 \ \mathrm {p.u.}\),\(\displaystyle \delta =\frac {\pi}{12} \ \mathrm {rad}\),\(P=1.23 \ \mathrm {p.u.}\),\(Q=0.195 \ \mathrm {p.u.}\)のときの\(x \ \mathrm {[p.u.]}\)と\(r \ \mathrm {[p.u.]}\)
(4)の\(\alpha \)と\(\beta \)の式に各値を代入して求めると,
\[
\begin{eqnarray}
\alpha &=& V_{1}V_{2}\sin \delta \\[ 5pt ]
&=& 1.05\times 1.01\times \sin \frac {\pi}{12} \\[ 5pt ]
&=& 1.05\times 1.01\times 0.25882 \\[ 5pt ]
&≒& 0.27448 \ \mathrm {[p.u.]} \\[ 5pt ]
\beta &=& V_{1}^{2}-V_{1}V_{2}\cos \delta \\[ 5pt ]
&=& 1.05^{2}-1.05\times 1.01\times \cos \frac {\pi}{12} \\[ 5pt ]
&=& 1.05^{2}-1.05\times 1.01\times 0.96593 \\[ 5pt ]
&≒& 0.078131 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\(x\)と\(r\)は,
\[
\begin{eqnarray}
x &=& \frac {P\alpha +Q\beta }{P^{2}+Q^{2}} \\[ 5pt ]
&=& \frac {1.23\times 0.27448+0.195 \times 0.078131 }{1.23^{2}+0.195^{2}} \\[ 5pt ]
&≒& \frac {0.33761+0.015236 }{1.5129+0.038025} \\[ 5pt ]
&≒& \frac {0.35285 }{1.5509} \\[ 5pt ]
&≒& 0.22751 → 0.228 \ \mathrm {[p.u.]} \\[ 5pt ]
r &=& \frac {P\beta -Q\alpha }{P^{2}+Q^{2}} \\[ 5pt ]
&=& \frac {1.23 \times 0.078131 -0.195\times 0.27448 }{1.23^{2}+0.195^{2}} \\[ 5pt ]
&≒& \frac {0.096101-0.053524 }{1.5129+0.038025} \\[ 5pt ]
&≒& \frac {0.04258 }{1.5509} \\[ 5pt ]
&≒& 0.027455 → 0.0275 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは