【質問】

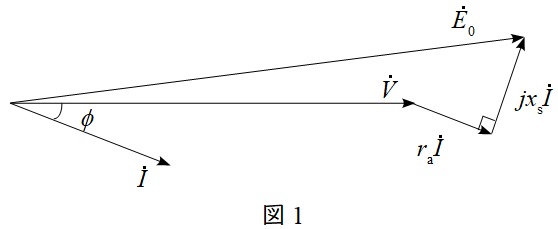
【回答】
ご質問ありがとうございます。
確かにこの解説では,かなりの計算内容が省略されていると思います。私の計算方法が100%正しいかどうか定かではありませんが,計算例として紹介します。
\[
\begin{eqnarray}
\varepsilon &=&\frac {\sqrt {\left( V+Ir_{\mathrm {a}}\cos \phi +Ix_{\mathrm {s}}\sin \phi \right) ^{2}+\left( Ix_{\mathrm {s}}\cos \phi -Ir_{\mathrm {a}}\sin \phi \right) ^{2}}-V}{V}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {V^{2}+\left( Ir_{\mathrm {a}}\cos \phi \right) ^{2} +\left( Ix_{\mathrm {s}}\sin \phi \right) ^{2}+2VIr_{\mathrm {a}}\cos \phi +2I^{2}r_{\mathrm {a}}x_{\mathrm {s}}\cos \phi \sin \phi +2VIx_{\mathrm {s}}\sin \phi +\left( Ix_{\mathrm {s}}\cos \phi \right) ^{2} -2I^{2}r_{\mathrm {a}}x_{\mathrm {s}}\cos \phi \sin \phi + \left( Ir_{\mathrm {a}}\sin \phi \right) ^{2}}-V}{V}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {V^{2}+\left( Ir_{\mathrm {a}}\right) ^{2} +\left( Ix_{\mathrm {s}}\right) ^{2}+2VIr_{\mathrm {a}}\cos \phi +2VIx_{\mathrm {s}}\sin \phi }-V}{V}\times 100 \left( ∵ \sin ^{2}\phi +\cos ^{2}\phi =1\right) \\[ 5pt ]
&=&\frac {V\sqrt {1+\left( \frac {Ir_{\mathrm {a}}}{V}\right) ^{2} +\left( \frac {Ix_{\mathrm {s}}}{V}\right) ^{2}+\frac {2Ir_{\mathrm {a}}\cos \phi }{V}+\frac {2Ix_{\mathrm {s}}\sin \phi }{V}}-V}{V}\times 100 \\[ 5pt ]
&≃&\frac {V\left[ 1+\frac {1}{2}\left( \frac {2Ir_{\mathrm {a}}\cos \phi }{V}+\frac {2Ix_{\mathrm {s}}\sin \phi}{V} \right) \right] -V}{V}\times 100 \\[ 5pt ]
&=&\frac {V+Ir_{\mathrm {a}}\cos \phi +Ix_{\mathrm {s}}\sin \phi -V }{V}\times 100 \\[ 5pt ]
&=&\frac {Ir_{\mathrm {a}}\cos \phi +Ix_{\mathrm {s}}\sin \phi }{V}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
となります。
一般的な近似計算の手法としては,\(\Delta ≪ 1\)の時,
\[
\begin{eqnarray}
\left( 1 + \Delta \right) ^{n}&≃&1 +n\Delta \\[ 5pt ]
\end{eqnarray}
\]
となります。例えば,\(n=2\)の時は,
\[
\begin{eqnarray}
\left( 1 + \Delta \right) ^{2}&=&1 +2\Delta +\Delta ^{2} \\[ 5pt ]
&≃&1 +2\Delta \\[ 5pt ]
\end{eqnarray}
\]
となります。本問においては\(\displaystyle \frac {Ir_{\mathrm {a}}}{V}, \frac {Ix_{\mathrm {s}}}{V} ≪ 1\)となり,計算中の\(\displaystyle \left( \frac {Ir_{\mathrm {a}}}{V}\right) ^{2}\)と\(\displaystyle \left( \frac {Ix_{\mathrm {s}}}{V}\right) ^{2}\)は上記\(\Delta ^{2}\)の考え方と同様に無視できることになります。





 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは