《機械・制御》〈自動制御〉[H26:問4]フィードバック制御系の伝達関数に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

図1はフィードバック制御系の基本構成を示し，\(G_{\mathrm {C}}(s)\)は補償器の伝達関数，\(G_{\mathrm {P}}(s)\)は制御対象の伝達関数を表している。また，\(R(s)\)，\(E(s)\)，\(D(s)\)及び\(Y(s)\)は，目標値\(r(t)\)，偏差\(e(t)\)，外乱\(d(t)\)及び制御量\(y(t)\)をそれぞれラプラス変換したものである。\(\displaystyle G_{\mathrm {C}}(s)=\frac {4(s+1)}{s+2}\)，\(\displaystyle G_{\mathrm {P}}(s)=\frac {1}{s(s^{2}+5s+5)}\)として，次の問に答えよ。

(1)　\(D(s)=0\)としたとき，\(R(s)\)から\(E(s)\)までの伝達関数を求めよ。

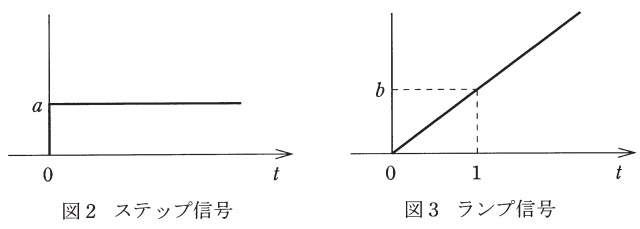
(2)　上記(1)において，目標値として図2に示す大きさ\(a \)のステップ信号を入力したときの定常偏差を求めよ。

(3)　上記(1)において，目標値として図3に示す傾き\(b\)のランプ信号を入力したときの定常偏差を求めよ。

(4)　\(R(s)=0\)としたとき，\(D(s)\)から\(Y(s)\)までの伝達関数を求めよ。

(5)　上記(4)において，外乱として図2に示す大きさ\(a\)のステップ信号を印加したとき，制御量の最終値を求めよ。

(6)　上記(4)において，外乱として図3に示す傾き\(b\)のランプ信号を印加したとき，制御量は発散することを示せ。

【ワンポイント解説】

本問は古典制御の比較的基本的な公式のみを使用した問題で，二種二次試験受験生であればかなりの数の受験生が完答できたのではないかと思われる問題です。計算間違いに注意して，確実に完答できるようにしましょう。

1.基本的なラプラス変換
\(f(t)\)のラプラス変換を\(F(s)\)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
a & \displaystyle \frac {a}{s} \\[ 5pt ] t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ] \mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ] \cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ] \sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ] \hline
\end{array}
\]

2.最終値の定理
\(f(t)\)の定常状態と\(F(s)\)には以下のような関係があります。
\[
\begin{eqnarray}
\displaystyle \lim_{ t \to \infty } f(t) = \displaystyle \lim_{ s \to 0 } sF(s) \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)\(D(s)=0\)としたとき，\(R(s)\)から\(E(s)\)までの伝達関数
図1のブロック図より，
\[
\begin{eqnarray}
R(s)-Y(s) &=& E(s)　&・・・・・①& \\[ 5pt ] E(s)G_{\mathrm {C}}(s)G_{\mathrm {P}}(s)&=& Y(s)　&・・・・・②& \\[ 5pt ] \end{eqnarray}
\] であるから，②を①に代入して\(Y(s)\)を消去すると，
\[
\begin{eqnarray}
R(s)-E(s)G_{\mathrm {C}}(s)G_{\mathrm {P}}(s) &=& E(s) \\[ 5pt ] R(s)&=& E(s) \left\{ 1+G_{\mathrm {C}}(s)G_{\mathrm {P}}(s) \right\} \\[ 5pt ] \frac {E(s)}{R(s)}&=& \frac {1}{1+G_{\mathrm {C}}(s)G_{\mathrm {P}}(s)} \\[ 5pt ] &=& \frac {1}{1+\frac {4(s+1)}{s+2}\cdot \frac {1}{s(s^{2}+5s+5)}} \\[ 5pt ] &=& \frac {s (s+2) (s^{2}+5s+5)}{s (s+2) (s^{2}+5s+5)+4(s+1)} \\[ 5pt ] &=& \frac {s^{4}+7s^{3}+15s^{2}+10s}{s^{4}+7s^{3}+15s^{2}+14s+4} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)大きさ\(a \)のステップ信号を入力したときの定常偏差
ワンポイント解説「1.基本的なラプラス変換」より，
\[
\begin{eqnarray}
\mathcal{L}[a] &=& \frac {a}{s} \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「2.最終値の定理」より\(e(t)\)の定常偏差は，
\[
\begin{eqnarray}
\displaystyle \lim_{ t \to \infty } e(t) &=& \displaystyle \lim_{ s \to 0 } sE(s) \\[ 5pt ] &=& \displaystyle \lim_{ s \to 0 } s\cdot \frac {s^{4}+7s^{3}+15s^{2}+10s}{s^{4}+7s^{3}+15s^{2}+14s+4}\cdot \frac {a}{s} \\[ 5pt ] &=& 0
\end{eqnarray}
\] と求められる。

(3)傾き\(b\)のランプ信号を入力したときの定常偏差
ワンポイント解説「1.基本的なラプラス変換」より，
\[
\begin{eqnarray}
\mathcal{L}[bt] &=& \frac {b}{s^{2}} \\[ 5pt ] \end{eqnarray}
\] であるから，(2)と同様に\(e(t)\)の定常偏差は，
\[
\begin{eqnarray}
\displaystyle \lim_{ t \to \infty } e(t) &=& \displaystyle \lim_{ s \to 0 } sE(s) \\[ 5pt ] &=& \displaystyle \lim_{ s \to 0 } s\cdot \frac {s^{4}+7s^{3}+15s^{2}+10s}{s^{4}+7s^{3}+15s^{2}+14s+4}\cdot \frac {b}{s^{2}} \\[ 5pt ] &=& \displaystyle \lim_{ s \to 0 } \frac {s^{3}+7s^{2}+15s^{1}+10}{s^{4}+7s^{3}+15s^{2}+14s+4}\cdot b \\[ 5pt ] &=& \frac {5}{2}b
\end{eqnarray}
\] と求められる。

(4)\(R(s)=0\)としたとき，\(D(s)\)から\(Y(s)\)までの伝達関数
各制御量の関係より，
\[
\begin{eqnarray}
\left\{ D(s)-Y(s)G_{\mathrm {C}}(s)\right\} G_{\mathrm {P}}(s) &=& Y(s) \\[ 5pt ] D(s)G_{\mathrm {P}}(s)-Y(s)G_{\mathrm {C}}(s)G_{\mathrm {P}}(s) &=& Y(s) \\[ 5pt ] D(s)G_{\mathrm {P}}(s) &=& Y(s)+Y(s)G_{\mathrm {C}}(s)G_{\mathrm {P}}(s) \\[ 5pt ] &=& Y(s)\left( 1+G_{\mathrm {C}}(s)G_{\mathrm {P}}(s)\right) \\[ 5pt ] \frac {Y(s)}{D(s)}&=& \frac {G_{\mathrm {P}}(s)}{ 1+G_{\mathrm {C}}(s)G_{\mathrm {P}}(s)} \\[ 5pt ] &=& \frac {\frac {1}{s(s^{2}+5s+5)}}{ 1+\frac {4(s+1)}{s+2}\cdot \frac {1}{s(s^{2}+5s+5)}} \\[ 5pt ] &=& \frac {s+2}{ s(s+2)(s^{2}+5s+5)+4(s+1)} \\[ 5pt ] &=& \frac {s+2}{s^{4}+7s^{3}+15s^{2}+14s+4} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)\(a\)のステップ信号を印加したとき，制御量の最終値
ワンポイント解説「1.基本的なラプラス変換」より，
\[
\begin{eqnarray}
\mathcal{L}[a] &=& \frac {a}{s} \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「2.最終値の定理」より制御量\(y(t)\)の最終値は，
\[
\begin{eqnarray}
\displaystyle \lim_{ t \to \infty } y(t) &=& \displaystyle \lim_{ s \to 0 } sY(s) \\[ 5pt ] &=& \displaystyle \lim_{ s \to 0 } s\cdot \frac {s+2}{s^{4}+7s^{3}+15s^{2}+14s+4}\cdot \frac {a}{s} \\[ 5pt ] &=& \frac {a}{2}
\end{eqnarray}
\] と求められる。

(6)傾き\(b\)のランプ信号を印加したとき，制御量は発散することを示す
ワンポイント解説「1.基本的なラプラス変換」より，
\[
\begin{eqnarray}
\mathcal{L}[bt] &=& \frac {b}{s^{2}} \\[ 5pt ] \end{eqnarray}
\] であるから，制御量\(y(t)\)の最終値は，
\[
\begin{eqnarray}
\displaystyle \lim_{ t \to \infty } y(t) &=& \displaystyle \lim_{ s \to 0 } sY(s) \\[ 5pt ] &=& \displaystyle \lim_{ s \to 0 } s\cdot \frac {s+2}{s^{4}+7s^{3}+15s^{2}+14s+4}\cdot \frac {b}{s^{2}} \\[ 5pt ] &=& \frac {2b}{0} \\[ 5pt ] &=& \infty \\[ 5pt ] \end{eqnarray}
\] と求められ，制御量\(y(t)\)は発散することが分かる。