【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,可動コイル形計器の測定範囲拡大に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
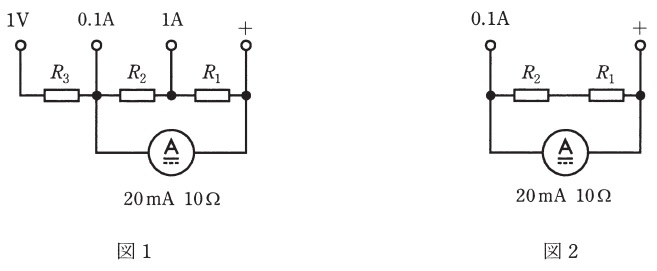
図1において,最大目盛値が\( \ 20 \ \mathrm {[mA]} \ \),内部抵抗が\( \ 10 \ \mathrm {[\Omega ]} \ \)の直流電流計に抵抗\( \ R_{\mathrm {1}} \ \),\( \ R_{\mathrm {2}} \ \),\( \ R_{\mathrm {3}} \ \)を接続し,電流測定範囲を拡大するとともに電圧を測定できるようにしたい。
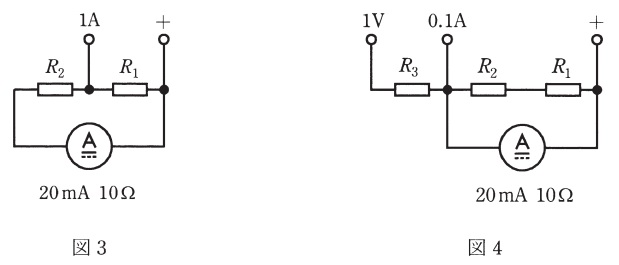
まず,電流の測定範囲を\( \ 0.1 \ \mathrm {[A]} \ \)及び\( \ 1 \ \mathrm {[A]} \ \)に拡大する場合には,図2及び図3のように\( \ R_{\mathrm {1}} \ \)及び\( \ R_{\mathrm {2}} \ \)を電流計に接続する。ここで,図2より\( \ R_{\mathrm {1}}+R_{\mathrm {2}}=\fbox { (1) } \ \mathrm {[\Omega ]} \ \)となり,図3より\( \ \fbox { (2) }\times R_{\mathrm {1}}=0.02\left( R_{2}+10\right) \ \)の関係が得られる。
以上より,\( \ R_{\mathrm {1}} \ \)及び\( \ R_{\mathrm {2}} \ \)を求めれば,\( \ R_{\mathrm {1}}=\fbox { (3) } \ \mathrm {[\Omega ]} \ \),\( \ R_{\mathrm {2}}=\fbox { (4) } \ \mathrm {[\Omega ]} \ \)となる。
さらに,電圧の測定範囲を\( \ 1 \ \mathrm {[V]} \ \)までにする場合には,図4より,\( \ R_{\mathrm {3}}=\fbox { (5) } \ \mathrm {[\Omega ]} \ \)を電流計に接続すればよいことがわかる。
〔問8の解答群〕
\[
\begin{eqnarray}
&(イ)& 0.23 &(ロ)& 0.25 &(ハ)& 0.30 \\[ 5pt ]
&(ニ)& 0.98 &(ホ)& 1.02 &(ヘ)& 1.37 \\[ 5pt ]
&(ト)& 1.67 &(チ)& 1.77 &(リ)& 1.96 \\[ 5pt ]
&(ヌ)& 2.00 &(ル)& 2.25 &(ヲ)& 2.50 \\[ 5pt ]
&(ワ)& 7.84 &(カ)& 8.00 &(ヨ)& 10.0 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
論理的な中身が理解できれば,キルヒホッフの法則のみで解けてしまう問題です。選択問題なので,選択しない受験生も多いかもしれませんが,受験生によって完答できるもしくは全く答えられないと言ったような点数差がはっきりと出てしまう問題とも言えます。
【解答】
(1)解答:ヲ
図2において電流の測定を最大にする場合,すなわち全体として\( \ 0.1 \ \mathrm {[A]} \ \)が流れる場合,電流計に流れる電流が\( \ 20 \ \mathrm {[mA]} \ \)であるから,\( \ R_{\mathrm {1}} \ \)及び\( \ R_{\mathrm {2}} \ \)に流れる電流\( \ I_{\mathrm {1}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {1}} &=&0.1-20\times 10^{-3} \\[ 5pt ]
&=&0.08 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,電流計の内部抵抗が\( \ 10 \ \mathrm {[\Omega ]} \ \)であるから,電流計にかかる電圧\( \ V_{\mathrm {1}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {1}} &=&10\times 20\times 10^{-3} \\[ 5pt ]
&=&0.2 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,これは\( \ R_{\mathrm {1}} \ \)及び\( \ R_{\mathrm {2}} \ \)にかかる電圧と等しくなる。よって,\( \ R_{\mathrm {1}}+R_{\mathrm {2}} \ \)の大きさは,
\[
\begin{eqnarray}
R_{\mathrm {1}}+R_{\mathrm {2}} &=&\frac {V_{\mathrm {1}}}{I_{\mathrm {1}}} \\[ 5pt ]
&=&\frac {0.2}{0.08} \\[ 5pt ]
&=&2.5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
図3において,全体として\( \ 1 \ \mathrm {[A]} \ \)が流れる場合,電流計に流れる電流が\( \ 20 \ \mathrm {[mA]} \ \)であるから,\( \ R_{\mathrm {1}} \ \)を流れる電流\( \ I_{\mathrm {2}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {2}} &=&1- 20\times 10^{-3} \\[ 5pt ]
&=&0.98 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,関係式は\( \ 0.98 R_{\mathrm {1}}=0.02\left( R_{2}+10\right) \ \)となる。
(3)解答:ロ
(2)の解答式を整理すると,
\[
\begin{eqnarray}
0.98 R_{\mathrm {1}} &=&0.02\left( R_{2}+10\right) \\[ 5pt ]
49 R_{\mathrm {1}} &=&R_{2}+10 \\[ 5pt ]
\end{eqnarray}
\]
となる。(1)より,
\[
\begin{eqnarray}
R_{\mathrm {1}}+R_{\mathrm {2}} &=&2.5 \\[ 5pt ]
R_{\mathrm {2}} &=&2.5-R_{\mathrm {1}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを代入すると,
\[
\begin{eqnarray}
49 R_{\mathrm {1}} &=&2.5-R_{\mathrm {1}}+10 \\[ 5pt ]
50 R_{\mathrm {1}} &=&12.5 \\[ 5pt ]
R_{\mathrm {1}} &=&0.25 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
\( \ R_{\mathrm {1}} =0.25 \ \mathrm {[\Omega ]} \ \)及び\( \ R_{\mathrm {1}}+R_{\mathrm {2}}= 2.5 \ \mathrm {[\Omega ]} \ \)より,
\[
\begin{eqnarray}
R_{\mathrm {2}} &=&2.5-R_{\mathrm {1}} \\[ 5pt ]
&=&2.5-0.25 \\[ 5pt ]
&=&2.25 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
図4において,電流計にかかる電圧の大きさが\( \ 20\times 10^{-3}\times 10 =0.2 \ \mathrm {[V]} \ \)であるから,\( \ R_{\mathrm {3}} \ \)にかかる電圧の大きさは,\( \ 0.8 \ \mathrm {[V]} \ \)となる。端子を繋ぎ変えた時,\( \ R_{\mathrm {3}} \ \)を流れる電流の大きさは\( \ 0.1 \ \mathrm {[A]} \ \)であるから,
\[
\begin{eqnarray}
R_{\mathrm {3}} &=&\frac {0.8}{0.1} \\[ 5pt ]
&=&8 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは