Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,同軸円筒導体中の電界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
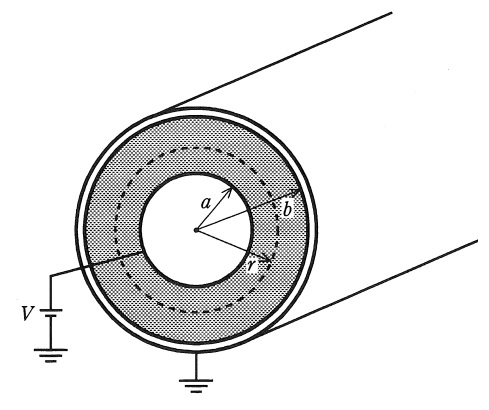
図のような同軸円筒導体を想定し,内部導体の外半径を\( \ a \ \),外部導体の内半径を\( \ b \ \),内外導体間の誘電体の誘電率を\( \ \varepsilon \ \)とする。外部導体を接地し,内部導体に電圧\( \ V \ \)を印加する場合を考える。このとき,誘電体内の最大電界を最小にする内部導体の外半径\( \ a \ \)の条件を求めたい。
まず,単位長さ当たりに内部導体に蓄えられている電荷\( \ q \ \)を求めることを考える。このとき,半径\( \ r \ \)の位置における電界の強さ\( \ E_{\mathrm {r}} \ \)と\( \ q \ \)との関係を求めると,次式のように表される。
\[
\begin{eqnarray}
E_{\mathrm {r}}&=& \ \fbox { (1) } ・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
これを\( \ r \ \)について\( \ a \ \)から\( \ b \ \)まで積分した値が,円筒間の電位差\( \ V \ \)に等しい。これにより\( \ V \ \)と\( \ q \ \)の関係が得られるため,内部導体に単位長さ当たりに蓄えられている電荷\( \ q \ \)は次式のように求められる。
\[
\begin{eqnarray}
q&=& \ \fbox { (2) } ・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
①及び②式から,内外導体間の電界の強さ\( \ E_{\mathrm {r}} \ \)の最大値\( \ E_{\mathrm {max}} \ \)は次式のように表される。
\[
\begin{eqnarray}
E_{\mathrm {max}}&=& \ \fbox { (3) } \\[ 5pt ]
\end{eqnarray}
\]
次に,\( \ b \ \)を一定としたときに,\( \ E_{\mathrm {max}} \ \)を最小にする内部導体の外半径\( \ a \ \)を求める。\( \ E_{\mathrm {max}} \ \)を最小にするには,この場合,\( \ \fbox { (3) } \ \)の分母を最大にする\( \ a \ \)を求めればよい。すなわち,\( \ \fbox { (3) } \ \)の分母を\( \ a \ \)で微分して,次式が成り立つ\( \ a \ \)を求めればよい。
\[
\begin{eqnarray}
\fbox { (4) } \ &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
よって,求める\( \ a \ \)の値は,次式で与えられる。ここで,自然対数の底を\( \ \mathrm {e}=2.718 \ \)とする。
\[
\begin{eqnarray}
a&=& \ \fbox { (5) } \\[ 5pt ]
\end{eqnarray}
\]
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {V}{\displaystyle b \ln \frac {b}{a}} &(ロ)& \frac {q}{2\pi \varepsilon r^{2}} &(ハ)& b \ln \frac {b}{a}+\frac {a^{2}}{b} \\[ 5pt ]
&(ニ)& 0.368b &(ホ)& \frac {2\pi \varepsilon Va^{2}b^{2}}{b^{2}-a^{2}} &(ヘ)& \ln \frac {b}{a}-1 \\[ 5pt ]
&(ト)& \frac {q}{2\pi \varepsilon r} &(チ)& \frac {4\pi \varepsilon Vab}{b-a} &(リ)& \frac {Vb}{a\left( b-a\right) } \\[ 5pt ]
&(ヌ)& 0.5b &(ル)& \frac {2\pi \varepsilon V}{\displaystyle \ln \frac {b}{a}} &(ヲ)& b^{0.368} \\[ 5pt ]
&(ワ)& \frac {V}{\displaystyle a \ln \frac {b}{a}} &(カ)& b-2a &(ヨ)& \frac {q}{4\pi \varepsilon r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
同軸円筒導体内の電界に関する問題です。
ケーブルで誘電体部の電界ができるだけ低くなるような導体の太さを模擬して検討している問題と言えるかと思います。
\( \ 2 \ \)種では本問のように電磁気で高い計算力が求められるので,計算力に自信のない方はまず数学の勉強をして,本問に臨んで下さい。
1.ガウスの定理
\( \ Q [ \mathrm {C} ] \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本であり,電界\( \ E \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの定理といいます。閉局面が同軸円筒導体で,単位長さ当たりに蓄えられている電荷\( \ q \ \)があれば,単位長さ当たりの電界\( \ E \ \)は,
\[
\begin{eqnarray}
2\pi r \times 1 \cdot E &=& \frac {q}{\varepsilon } \\[ 5pt ]
E &=& \frac {q}{2\pi \varepsilon r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.空間上の電位\( \ V \ \)
中心からの距離\( \ r \ \)に関する電界\( \ E_{\mathrm {r}} \ \)が与えられている時,その場所の電位\( \ V \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
3.積の微分の公式
\( \ y(x)=u(x)v(x) \ \)で与えられる関数があるとき,この関数の微分は,
\[
\begin{eqnarray}
\frac {\mathrm {d}y}{\mathrm {d}x}&=&\frac {\mathrm {d}u}{\mathrm {d}x}v+u\frac {\mathrm {d}v}{\mathrm {d}x} \\[ 5pt ]
&=&u^{\prime }v+uv^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:ト
ワンポイント解説「1.ガウスの定理」の通り,半径\( \ r \ \)の位置における電界の強さ\( \ E_{\mathrm {r}} \ \)は,
\[
\begin{eqnarray}
2\pi r \times 1 \cdot E_{\mathrm {r}} &=& \frac {q}{\varepsilon } \\[ 5pt ]
E_{\mathrm {r}} &=& \frac {q}{2\pi \varepsilon r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ル
円筒間の電位差\( \ V \ \)は,\( \ b \ \)を基準とした\( \ a \ \)の電位であるから,ワンポイント解説「2.空間上の電位\( \ V \ \)」より,
\[
\begin{eqnarray}
V&=&-\int _{b}^{a}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
&=&-\int _{b}^{a}\frac {q}{2\pi \varepsilon r}\mathrm {d}r \\[ 5pt ]
&=&-\frac {q}{2\pi \varepsilon }\int _{b}^{a}\frac {1}{r}\mathrm {d}r \\[ 5pt ]
&=&-\frac {q}{2\pi \varepsilon }\left[ \ln r \right] _{b}^{a} \\[ 5pt ]
&=&-\frac {q}{2\pi \varepsilon }\left( \ln a -\ln b\right) \\[ 5pt ]
&=&\frac {q}{2\pi \varepsilon }\left( \ln b -\ln a\right) \\[ 5pt ]
&=&\frac {q}{2\pi \varepsilon }\ln \frac {b}{a} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これより内部導体に単位長さ当たりに蓄えられている電荷\( \ q \ \)は,
\[
\begin{eqnarray}
V&=&\frac {q}{2\pi \varepsilon }\ln \frac {b}{a} \\[ 5pt ]
q&=&\frac {2\pi \varepsilon V}{\displaystyle \ln \frac {b}{a}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ワ
①,②式について\( \ q \ \)を消去すると,
\[
\begin{eqnarray}
E_{\mathrm {r}} &=& \frac {1}{2\pi \varepsilon r}\cdot \frac {2\pi \varepsilon V}{\displaystyle \ln \frac {b}{a}} \\[ 5pt ]
&=& \frac {1}{r}\cdot \frac {V}{\displaystyle \ln \frac {b}{a}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,内外導体間の電界の強さ\( \ E_{\mathrm {r}} \ \)の最大値\( \ E_{\mathrm {max}} \ \)は,\( \ r=a \ \)のときであり,
\[
\begin{eqnarray}
E_{\mathrm {max}} &=& \frac {1}{a}\cdot \frac {V}{\displaystyle \ln \frac {b}{a}} \\[ 5pt ]
&=& \frac {V}{\displaystyle a\ln \frac {b}{a}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヘ
(3)の解答式の分母\( \ f\left( a \right) =\displaystyle a\ln \frac {b}{a}=a\left( \ln b-\ln a \right) \ \)を微分すると,ワンポイント解説「3.積の微分の公式」の通り,
\[
\begin{eqnarray}
\frac {\mathrm {d}f\left( a \right) }{\mathrm {d}a} &=& \left( \ln b-\ln a \right) +a\cdot \left( -\frac {1}{a}\right) \\[ 5pt ]
&=& \ln \frac {b}{a} -1 \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ f\left( a \right) \ \)を最大にする\( \ \displaystyle \frac {\mathrm {d}f\left( a \right) }{\mathrm {d}a} \ \)は\( \ \displaystyle \frac {\mathrm {d}f\left( a \right) }{\mathrm {d}a}=0 \ \)の時なので,
\[
\begin{eqnarray}
\ln \frac {b}{a} -1 &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
の時,\( \ f\left( a \right) \ \)が最大となり,\( \ E_{\mathrm {max}} \ \)が最小となる。
(5)解答:ニ
(4)より,求める\( \ a \ \)の値は,
\[
\begin{eqnarray}
\ln \frac {b}{a} -1 &=& 0 \\[ 5pt ]
\ln \frac {b}{a} &=& 1 \\[ 5pt ]
\mathrm {e}^{1} &=& \frac {b}{a} \\[ 5pt ]
\mathrm {e} &=& \frac {b}{a} \\[ 5pt ]
a &=& \frac {b}{\mathrm {e}} \\[ 5pt ]
&=& \frac {b}{2.718} \\[ 5pt ]
&≒& 0.368b \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは