《機械》〈変圧器〉[H25:問2]三相変圧器の原理や特性に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，三相変圧器に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

定格容量$ \ 100 \ \mathrm {[kV\cdot A]} \ $，定格一次電圧$ \ 6 \ 600 \ \mathrm {[V]} \ $，定格二次電圧$ \ 200 \ \mathrm {[V]} \ $，定格周波数$ \ 50 \ \mathrm {[Hz]} \ $の$ \ \mathrm {Y – \Delta } \ $結線の三相変圧器がある。この変圧器を定格で使用したときの二次巻線の相電流は，$ \ \fbox {　（１）　} \ \mathrm {[A]} \ $である。一次電圧と二次電圧との位相差は$ \ \fbox {　（２）　} \ \mathrm {[rad]} \ $である。変圧器の励磁電流には，鉄心の非線形特性のために，高調波成分が含まれる。この内，電源周波数の$ \ \fbox {　（３）　} \ $倍の周波数成分は，三つの相で同相であり，二次巻線で還流する。

この変圧器の二次端子に$ \ 2 \ \mathrm {[\Omega ]} \ $の抵抗器$ \ 3 \ $台を星形結線で接続し，一次端子に定格電圧を印加した。変圧器の短絡インピーダンス及び励磁電流を無視したとき，一次電流は，$ \ \fbox {　（４）　} \ \mathrm {[A]} \ $となる。

この変圧器を同じ定格電圧の$ \ 60 \ \mathrm {[Hz]} \ $で使用することは$ \ \fbox {　（５）　} \ $。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　1.75　　　　　&（ロ）&　できる　　　　　&（ハ）&　\frac {\pi }{3} \\[ 5pt ] &（ニ）&　2　　　　　&（ホ）&　3　　　　　&（ヘ）&　\frac {\pi }{6} \\[ 5pt ] &（ト）&　3.03　　　　　&（チ）&　できない　　　　　&（リ）&　5 \\[ 5pt ] &（ヌ）&　5.25　　　　　&（ル）&　167　　　　&（ヲ）&　289 \\[ 5pt ] &（ワ）&　500　　　　　&（カ）&　\frac {\pi }{4}　　　　　&（ヨ）&　できるが容量が \ \frac {1}{1.2} \ 倍になる \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ 3 \ $種受験者だと正答率が悪くやや難しいレベルの問題となりますが，$ \ 2 \ $種受験者だと二次試験対策も行っているので，正答率が高くなる典型的な問題と言えると思います。変圧器は二次試験においても難解な計算が少ないので，本問の内容はよく理解しておくようにしましょう。

1.$ \ \mathrm {Y – \Delta } \ $結線方式の特徴
$ \ \mathrm {Y – \Delta } \ $結線方式は図1に示すような結線方式で，以下のような特徴があります。
①　$ \ \Delta \ $結線で第三調波成分を還流することができるので，二次側の電圧はひずみの少ない正弦波に近い波形となる。
②　一次，二次間の電圧で$ \ 30° \ $の位相差がある。

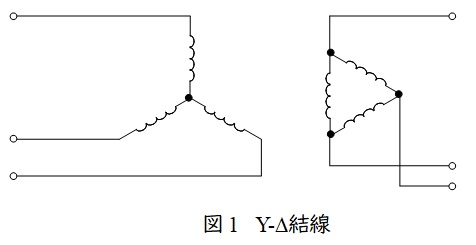
2.変圧器の誘導起電力
一次側の巻数を$ \ N_{1} \ $，二次側の巻数を$ \ N_{2} \ $，電源の周波数を$ \ f \ $，磁束の最大値を$ \ \phi \ $とすると，一次及び二次の誘導起電力$ \ E_{1} \ $及び$ \ E_{2} \ $は，
\[
\begin{eqnarray}
E_{1}&=&\frac {2\pi }{\sqrt {2}}fN_{1}\phi &=&4.44fN_{1}\phi \\[ 5pt ] E_{2}&=&\frac {2\pi }{\sqrt {2}}fN_{2}\phi &=&4.44fN_{2}\phi \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ル
定格容量$ \ P_{\mathrm {n}} = 100 \ \mathrm {[kV\cdot A]} \ $，定格二次電圧$ \ V_{\mathrm {2n}} = 200 \ \mathrm {[V]} \ $であるので，二次側の線電流$ \ I_{\mathrm {2n}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {2n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {2n}}} \\[ 5pt ] &=&\frac {100\times 10^{3}}{\sqrt {3}\times 200} \\[ 5pt ] &≒&288.68 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，相電流は，
\[
\begin{eqnarray}
\frac {I_{\mathrm {2n}}}{\sqrt {3}}&=&\frac {288.68}{\sqrt {3}} \\[ 5pt ] &≒&166.67　→　167 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヘ
ワンポイント解説「1.$ \ \mathrm {Y – \Delta } \ $結線方式の特徴」の通り，一次電圧と二次電圧の位相差は$ \ 30° \ $すなわち$ \ \displaystyle \frac {\pi }{6} \ $となります。

(3)解答：ホ
ワンポイント解説「1.$ \ \mathrm {Y – \Delta } \ $結線方式の特徴」の通り，電源周波数の$ \ 3 \ $倍の周波数成分は$ \ \Delta \ $結線で還流することができます。

(4)解答：イ
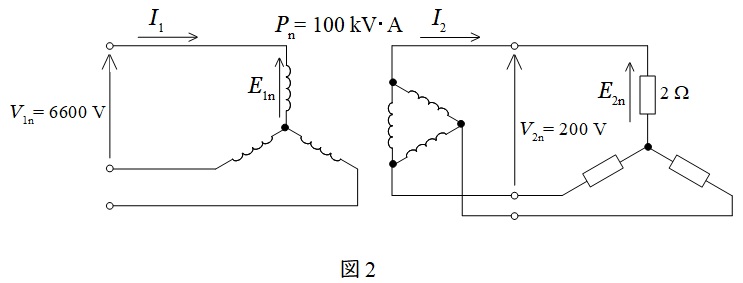
問題文に沿って図を描くと図2のようになる。
二次側の負荷にかかる電圧$ \ E_{\mathrm {2n}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {2n}}&=&\frac {V_{\mathrm {2n}}}{\sqrt {3}} \\[ 5pt ] &=&\frac {200}{\sqrt {3}} \\[ 5pt ] &≒&115.47 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であるから，二次側の線電流$ \ I_{\mathrm {2}} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {2}}&=&\frac {E_{\mathrm {2n}}}{2} \\[ 5pt ] &=&\frac {115.47}{2} \\[ 5pt ] &≒&57.735 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。変圧器の巻数比を$ \ a \ $とすると，
\[
\begin{eqnarray}
a&=&\frac {N_{1}}{N_{2}}=\frac {\displaystyle \frac {V_{\mathrm {1n}}}{\sqrt {3}}}{V_{\mathrm {2n}}}=\frac {\displaystyle \frac {I_{2}}{\sqrt {3}}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] の関係があるから，
\[
\begin{eqnarray}
I_{1}&=&\frac {V_{\mathrm {2n}}}{\displaystyle \frac {V_{\mathrm {1n}}}{\sqrt {3}}}\cdot \displaystyle \frac {I_{2}}{\sqrt {3}} \\[ 5pt ] &=&\frac {V_{\mathrm {2n}}}{V_{\mathrm {1n}}}I_{2} \\[ 5pt ] &=&\frac {200}{6600}\times 57.735 \\[ 5pt ] &≒&1.7495　→　1.75 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ロ
ワンポイント解説「2.変圧器の誘導起電力」より，
\[
\begin{eqnarray}
E_{1}&=&\frac {2\pi }{\sqrt {2}}fN_{1}\phi &=&4.44fN_{1}\phi \\[ 5pt ] E_{2}&=&\frac {2\pi }{\sqrt {2}}fN_{2}\phi &=&4.44fN_{2}\phi \\[ 5pt ] \end{eqnarray}
\] すなわち，
\[
\begin{eqnarray}
\phi &=&\frac {E_{1}}{4.44fN_{1}} \\[ 5pt ] \phi &=&\frac {E_{2}}{4.44fN_{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があり，変圧器の鎖交磁束は周波数に反比例する。したがって，周波数が大きくなる分には鉄心の磁気飽和は発生せず，使用上問題はない。