Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,同期発電機の特性曲線に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
1.無負荷飽和曲線
同期発電機を定格回転速度,無負荷で運転している場合の界磁電流に対する\( \ \fbox { (1) } \ \)の関係を示す曲線を無負荷飽和曲線という。界磁電流の増加に伴い鉄心が飽和するため,界磁電流と\( \ \fbox { (1) } \ \)の関係は比例関係にならず,いわゆる飽和特性を示す曲線になる。
2.短絡特性曲線
同期発電機の端子を短絡し,定格回転速度で運転した場合の,界磁電流に対する\( \ \fbox { (2) } \ \)の関係を示す曲線を短絡特性曲線という。端子短絡状態では,電機子反作用による\( \ \fbox { (3) } \ \)で界磁起磁力の大部分が打ち消されるため界磁電流を増加させても鉄心は磁気飽和せず,特性曲線はほぼ直線となる。
無負荷飽和曲線と短絡特性曲線が得られると,同期発電機の短絡比を求めることができ,この短絡比と単位法(\( \ \mathrm {p.u.} \ \))で表した\( \ \fbox { (4) } \ \)は互いに逆数の関係になる。
3.負荷飽和曲線
同期発電機を定格回転速度で運転し,電機子電流一定で力率一定の負荷をかけた場合の界磁電流に対する\( \ \fbox { (1) } \ \)の関係を示す曲線を負荷飽和曲線という。負荷飽和曲線のなかで特に電機子電流値が定格で\( \ \fbox { (5) } \ \)の負荷をかけた場合の曲線を\( \ \fbox { (5) } \ \)飽和曲線といい,無負荷飽和曲線をポーシェの三角形を用いて平行移動することでもこの飽和曲線を描くことができる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& 出力 &(ロ)& 交差磁化作用 &(ハ)& 定トルク \\[ 5pt ]
&(ニ)& 端子電圧 &(ホ)& 減磁作用 &(ヘ)& 零相電流 \\[ 5pt ]
&(ト)& 零力率 &(チ)& 電機子電流 &(リ)& 短絡インピーダンス \\[ 5pt ]
&(ヌ)& 過渡リアクタンス &(ル)& 差動電流 &(ヲ)& 容量性 \\[ 5pt ]
&(ワ)& 同期インピーダンス &(カ)& 反磁性効果 &(ヨ)& 励磁電圧 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
同期発電機の特性を問う問題で,(5)はほとんどの参考書に記載のない内容であるため,(1)~(4)が確実に解ければ問題ないと思います。
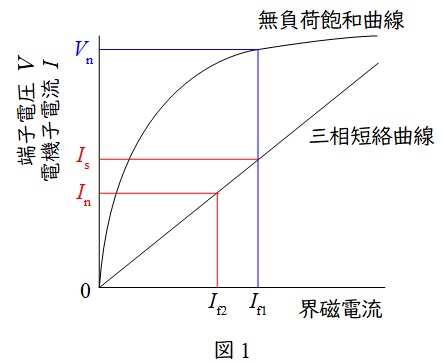
1.同期発電機の無負荷飽和曲線と三相短絡曲線
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。図中の\( \ V_{\mathrm {n}} \ \)は定格電圧,\( \ I_{\mathrm {n}} \ \)は定格電流,三相短絡曲線は曲線ですが,ほぼ比例の直線と近似できます。
この時,短絡比\( \ K \ \)は,
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.単位法によるインピーダンス\( \ Z \ \mathrm {[p.u.]} \ \)
図1において同期インピーダンス\( \ Z \ \)と単位法によるインピーダンス\( \ Z \ \mathrm {[p.u.]} \ \)は次式のように求められます。
\[
\begin{eqnarray}
Z&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{I_{\mathrm {s}}}&=&\frac {V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} &=& \frac {Z}{Z_{\mathrm {n}}}\\[ 5pt ]
&=& \frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} \\[ 5pt ]
&=& \frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {s}}}I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} \\[ 5pt ]
&=& \frac {I_{\mathrm {n}}}{I_{\mathrm {s}}} \\[ 5pt ]
&=& \frac {1}{K} \\[ 5pt ]
\end{eqnarray}
\]
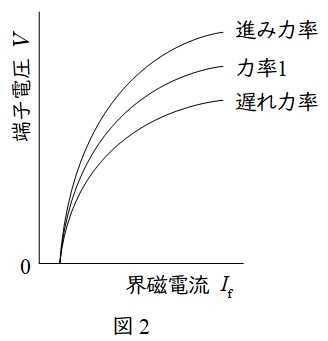
3.同期発電機の負荷飽和曲線
同期発電機の負荷飽和曲線は図2のようになります。
無負荷飽和曲線との違いは,同期インピーダンス分の電圧降下があるため,原点を通っていないことと,電機子反作用が進み力率では増磁作用,遅れ力率では減磁作用があるため,端子電圧がその分増加もしくは減少するという特徴があります。
【解答】
(1)解答:ニ
題意より解答候補は,(イ)出力,(ニ)端子電圧,(ヘ)零相電流,(チ)電機子電流,(ル)差動電流,(ヨ)励磁電圧,になると思います。ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り,無負荷飽和曲線は,界磁電流と端子電圧の関係となります。
(2)解答:チ
題意より解答候補は,(イ)出力,(ニ)端子電圧,(ヘ)零相電流,(チ)電機子電流,(ル)差動電流,(ヨ)励磁電圧,になると思います。ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り,短絡特性は,界磁電流と電機子電流の関係となります。
(3)解答:ホ
題意より解答候補は,(ロ)交差磁化作用,(ホ)減磁作用,(カ)反磁性効果,になると思います。端子短絡状態では,減磁作用で界磁起磁力の大部分が打ち消されるため界磁電流を増加させても鉄心は界磁磁束は磁気飽和しません。
(4)解答:ワ
題意より解答候補は,(リ)短絡インピーダンス,(ヌ)過渡リアクタンス,(ワ)同期インピーダンス,になると思います。ワンポイント解説「2.単位法によるインピーダンス\( \ Z \ \mathrm {[p.u.]} \ \)」の通り,短絡比と逆数の関係にあるのは単位法(\( \ \mathrm {p.u.} \ \))で表した同期インピーダンスとなります。
(5)解答:ト
題意より解答候補は,(ハ)定トルク,(ト)零力率,(ヲ)容量性,になると思います。負荷飽和曲線のなかで特に電機子電流値が定格で零力率の負荷をかけた場合の曲線を零力率飽和曲線と呼びます。ワンポイント解説「3.同期発電機の負荷飽和曲線」の内容を理解していれば,力率の内容であることの推測がつくと思います。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは