《機械》〈回転機〉[H29:問5] 三相誘導電動機の基本的な特性に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，三相誘導電動機の基本的な特性に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

巻線形三相誘導電動機の二次端子を開放した状態で，一次巻線に一定周波数$ \ f_{1} \ $の三相正弦波交流電圧を印加すると，$ \ \fbox {　（１）　} \ $は流れるが，二次電流が流れないので回転子は回転しない。二次端子を短絡すると二次電流が流れ，これと一次電流により発生する$ \ \fbox {　（２）　} \ $とによって，回転子にトルクが発生し，回転子は回転し始める。
回転子が滑り$ \ s \ $で回転している場合、同期速度を$ \ n_{0} \ $とすれば回転子の回転速度は$ \ \fbox {　（３）　} \ $で表され，このとき，二次巻線に発生する周波数は$ \ \fbox {　（４）　} \ $である。
回転子に負荷を接続し，その負荷を増大させると回転速度は低下する。すなわち，滑りは$ \ \fbox {　（５）　} \ $になり二次巻線に発生する起電力が大きくなる。その結果，二次電流が増加し，負荷トルクと平衡するだけの大きさのトルクを発生する。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　sn_{0}　　　　　&（ロ）&　\left( 1-s\right) n_{0}　　　　　&（ハ）&　短絡電流 \\[ 5pt ] &（ニ）&　減少すること　　　　　&（ホ）&　励磁電流　　　　　&（ヘ）&　\frac {f_{1}}{s} \\[ 5pt ] &（ト）&　ほぼ一定　　　　　&（チ）&　sf_{1}　　　　　&（リ）&　\left( 1-s\right) f_{1} \\[ 5pt ] &（ヌ）&　回転磁界　　　　　&（ル）&　負荷電流　　　　　&（ヲ）&　一次周波数 \\[ 5pt ] &（ワ）&　\frac {n_{0}}{s}　　　　　&（カ）&　増加すること　　　　　&（ヨ）&　回転速度
\end{eqnarray}
\]

【ワンポイント解説】

誘導電動機の二次側等価回路と一相分L型等価回路を描けるようにしておけば解けると思います。誘導電動機は二次試験でも頻出の分野なのでよく理解しておきましょう。

1.三相誘導電動機の一相分二次等価回路

\[
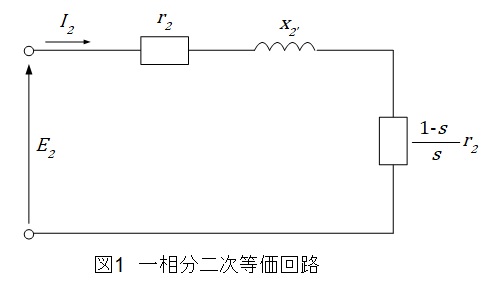
E_{2}:二次誘導起電力　r_{2}：二次抵抗　x_{2}：二次リアクタンス　s：滑り
\] この回路において，
\[
\begin{eqnarray}
&銅&損P_{\mathrm {c}}&：&r_{2}I_{2}^{2} \\[ 5pt ] &二&次出力P_{\mathrm {o}}　　&:& \frac {1-s}{s} r_{2} I_{2}^{2} \\[ 5pt ] &二&次入力P_{\mathrm {i}}　　&:&P_{\mathrm {i}}=P_{\mathrm {o}}+P_{\mathrm {c}}=\frac {r_{2}}{s} I_{2}^{2}
\end{eqnarray}
\] となります。

2.三相誘導電動機の一相分$ \ \mathrm {L} \ $形等価回路

\[
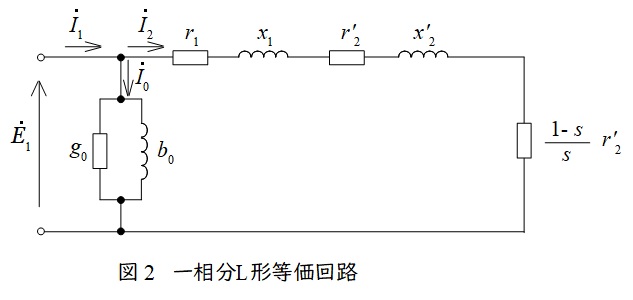
\begin{eqnarray}
&{\dot E}_{1}:&一次相電圧 \\[ 5pt ] &{\dot I}_{1}:&一次電流 \\[ 5pt ] &r_{1}:&一次抵抗 \\[ 5pt ] &x_{1}:&一次リアクタンス \\[ 5pt ]　
&{\dot I}_{2}:&負荷電流 \\[ 5pt ] &r_{2}:&一次側に換算した二次抵抗 \\[ 5pt ] &x_{2}:&一次側に換算した二次リアクタンス \\[ 5pt ] &{\dot I}_{0}:&励磁電流 \\[ 5pt ] &g_{0}:&励磁コンダクタンス \\[ 5pt ] &b_{0}:&励磁サセプタンス
\end{eqnarray}
\]

【解答】

(1)解答：ホ
題意より，解答候補は（ハ）短絡電流，（ホ）励磁電流，（ル）負荷電流，となります。図2の$ \ \mathrm {L} \ $形等価回路より二次端子を開放すると，$ \ {\dot I}_{2} \ $はゼロとなりますが，励磁電流$ \ {\dot I}_{0} \ $は流れます。よって解答は（ホ）励磁電流となります。

(2)解答：ヌ
電動機はフレミングの左手の法則に沿って，回転磁界と一次電流によってトルクが発生します。したがって，解答は（ヌ）回転磁界となります。

(3)解答：ロ
すべり$ \ s \ $の定義は，同期速度を$ \ n_{0} \ $，回転速度を$ \ n \ $として，
\[
s=\frac {n_{0}-n}{n_{0}}
\] なので，$ \ n \ $について整理すると，
\[
n=\left( 1-s\right)n_{0}
\] となります。

(4)解答：チ
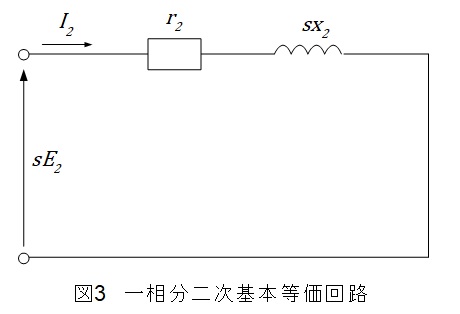
図1の元となる電動機の基本等価回路は図3の通りとなります。(図1と図3は全く同じ回路です。計算して整理してみて下さい。)
電動機の誘導起電力は$ \ sE_{2} \ \mathrm {[V]} \ $であり，誘導起電力に比例する周波数$ \ f_{2} \ $も$ \ f_{2}=sf_{1} \ $となります。