《電力・管理》〈水力〉[H24:問1]１台のポンプ水車と発電電動機による揚水発電所に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

$ \ 1 \ $台のポンプ水車と発電電動機による揚水発電所について，次の問に答えよ。ただし，諸元は次のとおりとし，貯水池水位の変動に伴う有効落差の変化はないものとする。

\[
\begin{array}{|l|c|r|c|}
\hline
　　項　目 & 記号 & 数　値 \ & 単　位 \\
\hline
有効貯水池容量 & V & 2\times 10^{6} & \left[ \mathrm {m^{3}}\right] \\
\hline
満水時静落差 & H & 150 & \left[ \mathrm {m}\right] \\
\hline
発電時水路損失 & H_{\mathrm {L}} & 10 & \left[ \mathrm {m}\right] \\
\hline
重力加速度 & \mathit {ｇ} & 9.8 & \left[ \mathrm {m/s^{2}}\right] \\
\hline
水の密度 & \rho & 1 \ 000 & \left[ \mathrm {kg/m^{3}}\right] \\
\hline
主変圧器容量 & T & 150 & \left[ \mathrm {MV\cdot A}\right] \\
\hline
\end{array}
\] \[
\begin{array}{|l|c|c|}
\hline
　　項　目 & 記　号 & 数　値 \\
\hline
電動機効率　　 & \eta _{\mathrm {M}} & 0.97 \\
\hline
発電機効率 & \eta _{\mathrm {G}} & 0.95 \\
\hline
ポンプ効率 & \eta _{\mathrm {P}} & 0.88 \\
\hline
水車効率 & \eta _{\mathrm {T}} & 0.90 \\
\hline
電動機力率 & \phi _{\mathrm {M}} & 1.00 \\
\hline
発電機力率 & \phi _{\mathrm {G}} & 0.80 \\
\hline
\end{array}
\]

(1)　電動機の最大皮相電力を$ \ S_{\mathrm {M}} \ \left[ \mathrm {MV\cdot A}\right] \ $，電動機出力（ポンプ入力）を機械最大出力$ \ P_{\mathrm {M}} \ \left[ \mathrm {MW}\right] \ $，電動機入力を$ \ P_{\mathrm {Mi}} \ \left[ \mathrm {MW}\right] \ $，発電機容量を$ \ S_{\mathrm {G}} \ \left[ \mathrm {MV\cdot A}\right] \ $，発電機の最大出力を$ \ P_{\mathrm {G}} \ \left[ \mathrm {MW}\right] \ $とした場合，次の関係式の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる記号を答えよ。
\[
\begin{eqnarray}
・P_{\mathrm {M}}&=&P_{\mathrm {Mi}}\times \boxed {　　\mathrm {A}　　} \\[ 5pt ] ・P_{\mathrm {Mi}}&=&\boxed {　　\mathrm {B}　　} \times \boxed {　　\mathrm {C}　　} \\[ 5pt ] ・P_{\mathrm {G}}&=&\boxed {　　\mathrm {D}　　} \times \boxed {　　\mathrm {E}　　} \\[ 5pt ] \end{eqnarray}
\]

(2)　さらに，発電機容量$ \ S_{\mathrm {G}} \ \left[ \mathrm {MV\cdot A}\right] \ $が電動機の最大皮相電力$ \ S_{\mathrm {M}} \ \left[ \mathrm {MV\cdot A}\right] \ $と同じとした場合，発電使用水量$ \ Q_{\mathrm {G}} \ \left[ \mathrm {m^{3} / s}\right] \ $を$ \ P_{\mathrm {M}} \ $など与えられた記号を用いて表せ。

(3)　(2)の条件において，$ \ P_{\mathrm {M}}=100 \ \left[ \mathrm {MW}\right] \ $の場合の発電使用水量$ \ Q_{\mathrm {G}} \ $を計算せよ。

(4)　(3)の条件において，有効貯水池容量をすべて使用するときの発電時間を計算せよ。

【ワンポイント解説】

揚水発電所の出力や使用水量に関する出題で，計算量もそれほど多くないため，多くの受験生が選択した問題であると思います。
水力発電所の発電出力の公式$ \ 9.8QH\eta \ \mathrm {[ kW ] } \ $の$ \ 9.8 \ $が重力加速度$ \ \mathit {ｇ} \ $に水の密度$ \ \rho \ $をかけて，$ \ \mathrm {[ W ] } \ $を$ \ \mathrm {[ kW ] } \ $にするために$ \ 1000 \ $で割ったものであることは理解しておきましょう。
また，単位が$ \ \mathrm {[ MW ] } \ $であること等も引っ掛けとなっているので，記号を扱う際に注意するようにしましょう。

1.揚水発電所の諸公式
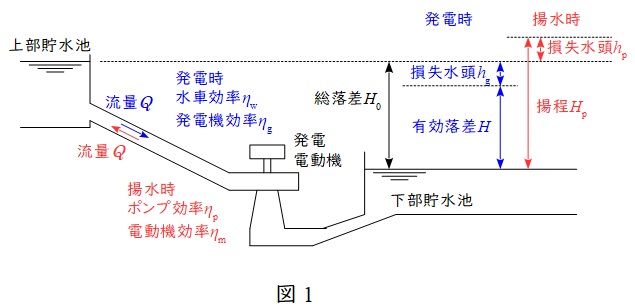
図1のように各諸元が与えられているとき，発電電力，揚水時必要動力及び総合効率は以下の通り求められます。

①発電電力$ \ P_{\mathrm {g}} \ \mathrm {[ kW ] } \ $
有効落差　：$H=H_{0}-h_{\mathrm {g}} \ \mathrm {[ m ] }$
発電機出力：$P_{\mathrm {g}}=9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[ kW ] }$

②揚水時必要動力$ \ P_{\mathrm {m}} \ \mathrm {[ kW ] } \ $
必要揚程　：$\displaystyle H_{\mathrm {p}}=H_{0}+h_{\mathrm {p}} \ \mathrm {[ m ] }$
所要動力　：$\displaystyle P_{\mathrm {m}}=\frac { 9.8QH_{\mathrm {p}}}{\eta _{\mathrm {p}} \eta _{\mathrm {m}}} \ \mathrm {[ kW ] }$

③揚水発電所総合効率$ \ \eta \ $
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {g}}}{P_{\mathrm {m}}} \\[ 5pt ] &=&\frac {9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}}}{\displaystyle \frac { 9.8QH_{\mathrm {p}}}{\eta _{\mathrm {p}} \eta _{\mathrm {m}}}} \\[ 5pt ] &=&\frac {H}{H_{\mathrm {p}}}\eta _{\mathrm {w}}\eta _{\mathrm {g}}\eta _{\mathrm {p}} \eta _{\mathrm {m}} \\[ 5pt ] &=&\frac {H_{0}-h_{\mathrm {g}}}{H_{0}+h_{\mathrm {p}}}\eta _{\mathrm {w}}\eta _{\mathrm {g}}\eta _{\mathrm {p}} \eta _{\mathrm {m}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)各関係式の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる記号
$ \ \boxed {　　\mathrm {A}　　} \ $
電動機出力$ \ P_{\mathrm {M}} \ \left[ \mathrm {MW}\right] \ $は電動機入力$ \ P_{\mathrm {Mi}} \ \left[ \mathrm {MW}\right] \ $と電動機効率$ \ \eta _{\mathrm {M}} \ $を用いると，
\[
\begin{eqnarray}
P_{\mathrm {M}} &=&P_{\mathrm {Mi}}\times \eta _{\mathrm {M}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

$ \ \boxed {　　\mathrm {B}　　} \ $，$ \ \boxed {　　\mathrm {C}　　} \ $
電動機の最大皮相電力が$ \ S_{\mathrm {M}} \ \left[ \mathrm {MV\cdot A}\right] \ $，電動機の力率が$ \ \phi _{\mathrm {M}} \ $であるから，電動機入力$ \ P_{\mathrm {Mi}} \ \left[ \mathrm {MW}\right] \ $は，
\[
\begin{eqnarray}
P_{\mathrm {Mi}} &=&S_{\mathrm {M}}\times \phi _{\mathrm {M}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

$ \ \boxed {　　\mathrm {D}　　} \ $，$ \ \boxed {　　\mathrm {E}　　} \ $
発電機容量が$ \ S_{\mathrm {G}} \ \left[ \mathrm {MV\cdot A}\right] \ $，発電機の力率が$ \ \phi _{\mathrm {G}} \ $であるから，発電機の最大出力$ \ P_{\mathrm {G}} \ \left[ \mathrm {MW}\right] \ $は，
\[
\begin{eqnarray}
P_{\mathrm {G}} &=&S_{\mathrm {G}}\times \phi _{\mathrm {G}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)$ \ S_{\mathrm {G}} \ \left[ \mathrm {MV\cdot A}\right] \ $が$ \ S_{\mathrm {M}} \ \left[ \mathrm {MV\cdot A}\right] \ $と同じとした場合，発電使用水量$ \ Q_{\mathrm {G}} \ \left[ \mathrm {m^{3} / s}\right] \ $
(1)の各式より，
\[
\begin{eqnarray}
S_{\mathrm {M}} &=&\frac {P_{\mathrm {Mi}}}{\phi _{\mathrm {M}}} \\[ 5pt ] S_{\mathrm {G}} &=&\frac {P_{\mathrm {G}}}{\phi _{\mathrm {G}}} \\[ 5pt ] \end{eqnarray}
\] であるから，$ \ S_{\mathrm {G}}=S_{\mathrm {M}} \ $より，
\[
\begin{eqnarray}
\frac {P_{\mathrm {G}}}{\phi _{\mathrm {G}}} &=&\frac {P_{\mathrm {Mi}}}{\phi _{\mathrm {M}}} \\[ 5pt ] P_{\mathrm {G}}&=&\frac {P_{\mathrm {Mi}}\phi _{\mathrm {G}}}{\phi _{\mathrm {M}}} \\[ 5pt ] &=&\frac {P_{\mathrm {M}}\phi _{\mathrm {G}}}{\eta _{\mathrm {M}}\phi _{\mathrm {M}}} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，ワンポイント解説「1.揚水発電所の諸公式」より，有効落差$ \ H_{\mathrm {e}} \ \mathrm {[ m ] } \ $とすると，
\[
\begin{eqnarray}
P_{\mathrm {G}}&=&\rho \mathit {ｇ} Q_{\mathrm {G}}H_{\mathrm {e}}\eta _{\mathrm {T}}\eta _{\mathrm {G}}\times 10^{-6} \\[ 5pt ] &=&\rho \mathit {ｇ} Q_{\mathrm {G}}\left( H-H_{\mathrm {L}}\right) \eta _{\mathrm {T}}\eta _{\mathrm {G}}\times 10^{-6} \\[ 5pt ] \end{eqnarray}
\] となるから，
\[
\begin{eqnarray}
\rho \mathit {ｇ} Q_{\mathrm {G}}\left( H-H_{\mathrm {L}}\right) \eta _{\mathrm {T}}\eta _{\mathrm {G}}\times 10^{-6} &=&\frac {P_{\mathrm {M}}\phi _{\mathrm {G}}}{\eta _{\mathrm {M}}\phi _{\mathrm {M}}} \\[ 5pt ] Q_{\mathrm {G}}&=&\frac {P_{\mathrm {M}}\phi _{\mathrm {G}}}{\rho \mathit {ｇ} \left( H-H_{\mathrm {L}}\right) \eta _{\mathrm {T}}\eta _{\mathrm {G}}\eta _{\mathrm {M}}\phi _{\mathrm {M}}}\times 10^{6} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)$ \ P_{\mathrm {M}}=100 \ \left[ \mathrm {MW}\right] \ $の場合の発電使用水量$ \ Q_{\mathrm {G}} \ $
(2)の解答式に各値を代入すると，
\[
\begin{eqnarray}
Q_{\mathrm {G}}&=&\frac {P_{\mathrm {M}}\phi _{\mathrm {G}}}{\rho \mathit {ｇ} \left( H-H_{\mathrm {L}}\right) \eta _{\mathrm {T}}\eta _{\mathrm {G}}\eta _{\mathrm {M}}\phi _{\mathrm {M}}}\times 10^{6} \\[ 5pt ] &=&\frac {100\times 0.80}{1000\times 9.8 \times \left( 150-10\right) \times 0.90 \times 0.95\times 0.97 \times 1.00 }\times 10^{6} \\[ 5pt ] &≒&70.307　→　70.3 \ \left[ \mathrm {m^{3} / s}\right] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)有効貯水池容量をすべて使用するときの発電時間
揚水貯水容量$ \ V=2\times 10^{6} \ \left[ \mathrm {m^{3} }\right] \ $であるから，発電時間$ \ T \ \left[ \mathrm {h }\right] \ $は，
\[
\begin{eqnarray}
T&=&\frac {V}{Q_{\mathrm {G}}\times 3600} \\[ 5pt ] &=&\frac {2\times 10^{6}}{70.307\times 3600} \\[ 5pt ] &≒&7.90 \ \left[ \mathrm {h}\right] \\[ 5pt ] \end{eqnarray}
\] と求められる。