《電力・管理》〈配電〉[H28:問4]1線地絡故障時の零相変流器に流れる電流に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

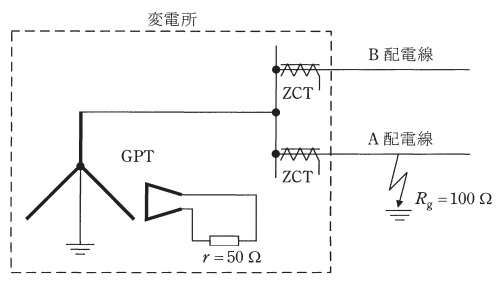
図のような\( \ \mathrm {6.6 \ kV} \ \)，\( \ \mathrm {50 \ Hz} \ \)の三相\( \ 3 \ \)線式配電線がある。\( \ \mathrm {A} \ \)配電線に\( \ 1 \ \)線地絡故障が発生した際，変電所に施設した\( \ \mathrm {A} \ \)配電線用零相変流器(\( \ \mathrm {ZCT} \ \))に流れる零相電流の合計値を，次の(1)～(4)に基づき答えよ。
ただし，配電線\( \ 1 \ \)線当たりの対地静電容量は\( \ \mathrm {0.01 \ \mu F/km} \ \)，配電線のこう長は\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)ともに\( \ \mathrm {5 \ km} \ \)，接地用変圧器(\( \ \mathrm {GPT} \ \))二次側の挿入抵抗\( \ r \ \)は\( \ \mathrm {50 \ \Omega } \ \)，\( \ \mathrm {GPT} \ \)の変成比は\( \ \mathrm {6600 \ V \ / \ 110 \ V} \ \)，配電線の電圧は\( \ \mathrm {6600 \ V} \ \)(平衡三相電圧)，地絡抵抗\( \ R_{\mathrm {g}} \ \)は\( \ \mathrm {100 \ \Omega } \ \)とし，その他定数は無視するものとする。

(1)　\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)配電線の\( \ 1 \ \)線当たりの対地アドミタンスを\( \ \dot Y \ \)，\( \ \mathrm {GPT} \ \)二次側挿入抵抗の一次側に換算した等価中性点抵抗を\( \ R_{\mathrm {n}} \ \)，地絡抵抗を\( \ R_{\mathrm {g}} \ \)，地絡故障が発生した線の故障発生前の対地電圧を\( \ {\dot E}_{\mathrm {a}} \ \)とするとき，\( \ 1 \ \)線地絡故障時の等価回路を示せ。

(3)　\( \ R_{\mathrm {n}} \ \)を\( \ \mathrm {GPT} \ \)の二次側挿入抵抗値から，一次側に換算した値で求めよ。

(4)　各値を用いて\( \ {\dot I}_{\mathrm {AG}} \ \)の大きさを計算せよ。

【ワンポイント解説】

\( \ 1 \ \)線地絡故障であると，対称座標法によって解く方法もありますが，本問の場合は重ね合わせの理による等価回路で解いた方がスムースに解けると思います。

1.テブナンの定理
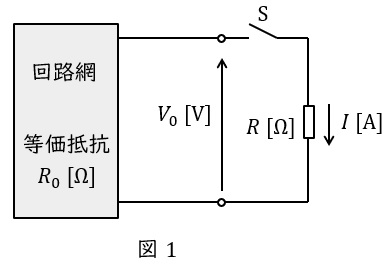
図1のような回路において，端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \)，端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする（ただし，電圧源は短絡，電流源は開放する）と，図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ] \end{eqnarray}
\] で求められます。この関係は抵抗のみでなく，リアクタンスにも適用可能です。

2.配電線\( \ 1 \ \)線地絡時の等価回路
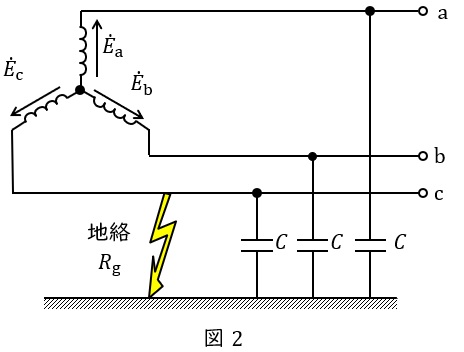
図2のような変圧器に接続された三相線路があり，\( \ \mathrm {c} \ \)相に\( \ 1 \ \)線地絡事故が発生したとします。
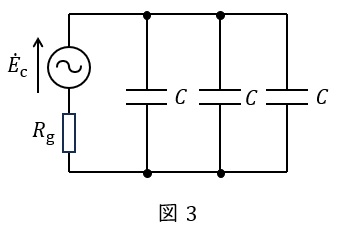
地絡点にテブナンの定理を適用すると，地絡点の開放電圧は\( \ {\dot E}_{\mathrm {c}} \ \)，地絡点から見たインピーダンスは電源を短絡して考えれば良いので，各相の静電容量が並列に接続された状態となります。したがって，等価回路は図3のように描くことができます。

【解答】

(1)\( \ 1 \ \)線地絡故障時の等価回路を示す
ワンポイント解説「2.配電線\( \ 1 \ \)線地絡時の等価回路」より，\( \ \mathrm {A} \ \)配電線と\( \ \mathrm {B} \ \)配電線，及び接地抵抗を考慮した等価回路は，図4のようになる。

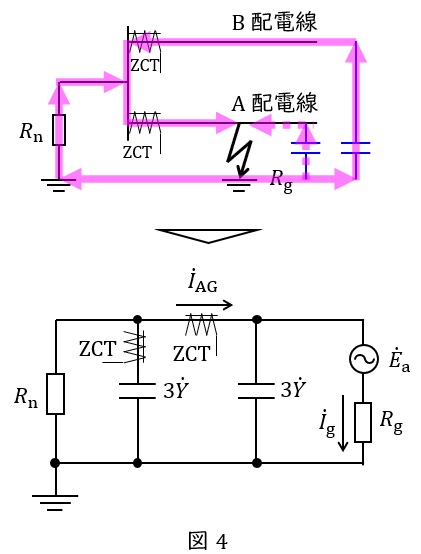
(2)地絡点からみたインピーダンス\( \ \dot Z \ \)及び\( \ \mathrm {A} \ \)配電線用\( \ \mathrm {ZCT} \ \)に流れる零相電流\( \ {\dot I}_{\mathrm {AG}} \ \)を等価回路から\( \ \dot Y \ \)，\( \ R_{\mathrm {n}} \ \)，\( \ R_{\mathrm {g}} \ \)及び\( \ {\dot E}_{\mathrm {a}} \ \)を用いて表す
図4の等価回路から，故障点から見た合成インピーダンス\( \ \dot Z \ \)は，
\[
\begin{eqnarray}
\dot Z&=&\frac {\displaystyle R_{\mathrm {n}}\cdot \frac {1}{3\dot Y+3\dot Y} }{\displaystyle R_{\mathrm {n}}+\frac {1}{3\dot Y+3\dot Y}} \\[ 5pt ] &=& \frac {R_{\mathrm {n}}}{1+6R_{\mathrm {n}}\dot Y}
\end{eqnarray}
\] と求められる。これより地絡電流\( \ {\dot I}_{\mathrm {G}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {G}}&=&\frac {{\dot E}_{\mathrm {a}}}{\dot Z+R_{\mathrm {g}}} \\[ 5pt ] &=&\cfrac {{\dot E}_{\mathrm {a}}}{\cfrac {R_{\mathrm {n}}}{1+6R_{\mathrm {n}}\dot Y}+R_{\mathrm {g}}} \\[ 5pt ] &=& \frac {1+6R_{\mathrm {n}}\dot Y}{R_{\mathrm {n}}+R_{\mathrm {g}}+6R_{\mathrm {n}}R_{\mathrm {g}}\dot Y}{\dot E}_{\mathrm {a}}
\end{eqnarray}
\] となる。\( \ \mathrm {A} \ \)配電線用\( \ \mathrm {ZCT} \ \)に流れる零相電流\( \ {\dot I}_{\mathrm {AG}} \ \)は，アドミタンスの分流比の計算から，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {AG}}&=&\cfrac {\cfrac {1}{R_{\mathrm {n}}}+3\dot Y}{\cfrac {1}{R_{\mathrm {n}}}+3\dot Y+3\dot Y}{\dot I}_{G} \\[ 5pt ] &=& \cfrac {1+3R_{\mathrm {n}}\dot Y}{1+6R_{\mathrm {n}}\dot Y}\cdot \cfrac {1+6R_{\mathrm {n}}\dot Y}{R_{\mathrm {n}}+R_{g}+6R_{\mathrm {n}}R_{\mathrm {g}}\dot Y}{\dot E}_{\mathrm {a}} \\[ 5pt ] &=& \frac {1+3R_{\mathrm {n}}\dot Y}{R_{\mathrm {n}}+R_{\mathrm {g}}+6R_{\mathrm {n}}R_{\mathrm {g}}\dot Y}{\dot E}_{\mathrm {a}}
\end{eqnarray}
\] と求められる。

(3)\( \ R_{\mathrm {n}} \ \)を\( \ \mathrm {GPT} \ \)の二次側挿入抵抗値から，一次側に換算した値で求める
二次側挿入抵抗\( \ r=50 \ \Omega \ \)であり，\( \ 1 \ \)相あたりの分担は，\( \ \displaystyle \frac {50}{3} \ \Omega \ \)であるから，一次側に換算した抵抗値\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&\left( \frac {6600}{110}\right) ^{2} \times \frac {50}{3} \\[ 5pt ] &=& 60000 \ [ \Omega ] \end{eqnarray}
\] となる。等価回路上の中性点抵抗\( \ R_{\mathrm {n}} \ \)は\( \ 3 \ \)相一括での抵抗値なので，
\[
\begin{eqnarray}
R_{\mathrm {n}}&=&\frac {R}{3} \\[ 5pt ] &=&\frac {60000}{3} \\[ 5pt ] &=& 20000 \ [ \Omega ] \end{eqnarray}
\] と求められる。

(4)\( \ {\dot I}_{\mathrm {AG}} \ \)の大きさを計算する
(2)の解答式に各値を代入すると，
\[
\begin{eqnarray}
\left| {\dot I}_{\mathrm {AG}}\right| &=&\left| \frac {1+3R_{\mathrm {n}}\dot Y}{R_{\mathrm {n}}+R_{\mathrm {g}}+6R_{\mathrm {n}}R_{\mathrm {g}}\dot Y}{\dot E}_{\mathrm {a}}\right| \\[ 5pt ] &=&\left| \frac {1+3\times 20000\times \mathrm {j}2\pi \times 50\times 0.01\times 10^{-6} \times 5}{20000+100+6\times 20000\times 100 \times \mathrm {j}2\pi \times 50\times 0.01\times 10^{-6} \times 5}\cdot \frac {6600}{\sqrt {3}}\right| \\[ 5pt ] &≒&\left| \frac {1+\mathrm {j}0.94248}{20100+ \mathrm {j} 188.50}\cdot \frac {6600}{\sqrt {3}}\right| \\[ 5pt ] &≒& \frac {\sqrt {1+0.94248^{2}}}{\sqrt{20100^{2}+ 188.50^{2}}}\cdot \frac {6600}{\sqrt {3}} \\[ 5pt ] &≒& \frac {1.3741}{20101}\cdot \frac {6600}{\sqrt {3}} \\[ 5pt ] &≒& 0.260 \ [ \mathrm{A} ] \\[ 5pt ] \end{eqnarray}
\] と求められる。