Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,\( \ RL \ \)回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
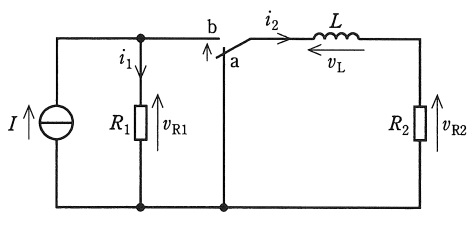
図のように,抵抗値が\( \ R_{1} \ \),\( \ R_{2} \ \),インダクタンスが\( \ L \ \)である素子,スイッチ及び直流電流源からなる回路がある。電流及び電圧を図のように定める。
時間\( \ t<0 \ \)ではスイッチは\( \ \mathrm {a} \ \)側にあり,回路は定常状態である。\( \ t=0 \ \)において,スイッチを\( \ \mathrm {a} \ \)から\( \ \mathrm {b} \ \)に切り替えた。\( \ t>0 \ \)における電圧\( \ v_{\mathrm {R1}} \ \)及び\( \ v_{\mathrm {L}} \ \)の時間的変化について考える。\( \ t>0 \ \)において,それぞれの電流,電圧の関係から次式が得られる。
\[
\begin{eqnarray}
&&i_{1}+i_{2}=I &・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
&&v_{\mathrm {R1}}=v_{\mathrm {L}}+v_{\mathrm {R2}} &・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
&&R_{1}i_{1}= \ \fbox { (1) } \ +R_{2}i_{2} &・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
\( \ t=0 \ \)における\( \ i_{2} \ \)は\( \ \fbox { (2) } \ \)であるので,これらの式より\( \ i_{2} \ \)について解くと,
\[
\begin{eqnarray}
i_{2}&=& \ \fbox { (3) } \\[ 5pt ]
\end{eqnarray}
\]
となる。また,
\[
\begin{eqnarray}
v_{\mathrm {L}}&=& \ \fbox { (4) } \\[ 5pt ]
\end{eqnarray}
\]
となる。
\( \ t=\infty \ \)における\( \ v_{\mathrm {R1}} \ \)は\( \ \fbox { (5) } \ \)となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{1}}{R_{1}+R_{2}}I &(ロ)& R_{1}I \\[ 5pt ]
&(ハ)& \frac {R_{1}}{R_{1}+R_{2}}I\left( 1-\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t}\right) &(ニ)& L\frac {\mathrm {d}i_{2}}{\mathrm {d}t} \\[ 5pt ]
&(ホ)& R_{2}I\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t} &(ヘ)& \frac {R_{1}R_{2}}{R_{1}+R_{2}}I \\[ 5pt ]
&(ト)& \frac {1}{L}\cdot \frac {\mathrm {d}i_{2}}{\mathrm {d}t} &(チ)& I \\[ 5pt ]
&(リ)& 0 &(ヌ)& \frac {R_{1}}{R_{1}+R_{2}}I\left( 1-\mathrm {e}^{-\frac {L}{R_{1}+R_{2}}t}\right) \\[ 5pt ]
&(ル)& R_{1}I\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t} &(ヲ)& \frac {R_{1}^{2}}{R_{1}+R_{2}}I \\[ 5pt ]
&(ワ)& R_{1}I\mathrm {e}^{-L\left( R_{1}+R_{2}\right) t} &(カ)& \frac {R_{1}}{R_{1}+R_{2}}I\left[ 1-\mathrm {e}^{-L\left( R_{1}+R_{2}\right) t}\right] \\[ 5pt ]
&(ヨ)& L\int i_{2}\mathrm {d}t && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ RL \ \)回路の過渡現象に関する問題です。
電源が電流源となっているので少し戸惑う方もいるかもしれませんが,解き方は通常の電圧源での解き方と変わりません。
パターンを覚えて確実に解けるようになりましょう。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
過渡現象における\( \ RLC \ \)それぞれの電圧は,線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \),リアクトル\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ]
v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,一般解\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解すなわち\( \ L \ \)開放(\( \ E=0 \ \)と同義)の時の解です。
これは,電流源に関しても同様に扱うことができます。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となった場合,両辺とも対数を外すと,
\[
\begin{eqnarray}
x&=&A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ニ
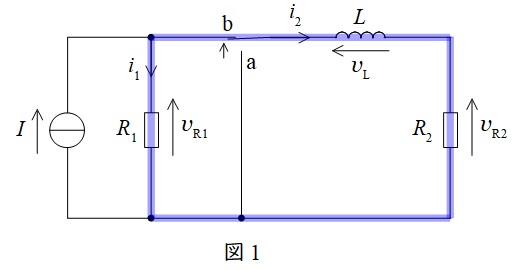
図1に示す閉回路について,回路方程式をたてると,ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」より,
\[
\begin{eqnarray}
R_{1}i_{1}&=&L\frac {\mathrm {d}i_{2}}{\mathrm {d}t}+R_{2}i_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:リ
\( \ t=0 \ \)における\( \ i_{2} \ \)は,\( \ \mathrm {a} \ \)側の回路に電源が接続されていないので,\( \ i_{2}=0 \ \)となる。
(3)解答:ハ
①を③に代入すると,
\[
\begin{eqnarray}
R_{1}i_{1}&=&L\frac {\mathrm {d}i_{2}}{\mathrm {d}t}+R_{2}i_{2} \\[ 5pt ]
R_{1}\left( I-i_{2}\right) &=&L\frac {\mathrm {d}i_{2}}{\mathrm {d}t}+R_{2}i_{2} \\[ 5pt ]
R_{1}I-R_{1}i_{2} &=&L\frac {\mathrm {d}i_{2}}{\mathrm {d}t}+R_{2}i_{2} \\[ 5pt ]
R_{1}I &=&L\frac {\mathrm {d}i_{2}}{\mathrm {d}t}+\left( R_{1}+R_{2}\right) i_{2} \\[ 5pt ]
L\frac {\mathrm {d}i_{2}}{\mathrm {d}t}+\left( R_{1}+R_{2}\right) i_{2} &=&R_{1}I \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.過渡現象における定常解と過渡解」の通り,微分方程式を解くと,定常解\( \ i_{\mathrm {2s}} \ \)は,
\[
\begin{eqnarray}
\left( R_{1}+R_{2}\right) i_{\mathrm {2s}} &=&R_{1}I \\[ 5pt ]
i_{\mathrm {2s}}&=&\frac {R_{1}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
となる。また,過渡解\( \ i_{\mathrm {2t}} \ \)は,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{\mathrm {2t}}}{\mathrm {d}t}+\left( R_{1}+R_{2}\right) i_{\mathrm {2t}} &=&0 \\[ 5pt ]
L\frac {\mathrm {d}i_{\mathrm {2t}}}{\mathrm {d}t} &=&-\left( R_{1}+R_{2}\right) i_{\mathrm {2t}} \\[ 5pt ]
\frac {1}{i_{\mathrm {2t}}}\mathrm {d}i_{\mathrm {2t}} &=&-\frac {R_{1}+R_{2}}{L} \mathrm {d}t \\[ 5pt ]
\ln i_{\mathrm {2t}}&=&-\frac {R_{1}+R_{2}}{L} t +C \\[ 5pt ]
i_{\mathrm {2t}}&=&A\mathrm {e}^{-\frac {R_{1}+R_{2}}{L} t } \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,一般解\( \ i_{\mathrm {2}} \ \)は,
\[
\begin{eqnarray}
i_{\mathrm {2}} &=&i_{\mathrm {2s}}+i_{\mathrm {2t}} \\[ 5pt ]
&=&\frac {R_{1}}{R_{1}+R_{2}}I+A\mathrm {e}^{-\frac {R_{1}+R_{2}}{L} t } \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ t=0 \ \)のとき\( \ i_{\mathrm {2}}\left( 0 \right) =0 \ \)であるから,
\[
\begin{eqnarray}
0&=&\frac {R_{1}}{R_{1}+R_{2}}I+A \\[ 5pt ]
A&=&-\frac {R_{1}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
i_{\mathrm {2}} &=&\frac {R_{1}}{R_{1}+R_{2}}I-\frac {R_{1}}{R_{1}+R_{2}}I\mathrm {e}^{-\frac {R_{1}+R_{2}}{L} t } \\[ 5pt ]
&=&\frac {R_{1}}{R_{1}+R_{2}}I\left( 1-\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
\( \ v_{\mathrm {L}}=\displaystyle L\frac {\mathrm {d}i_{2}}{\mathrm {d}t} \ \)であるから,
\[
\begin{eqnarray}
v_{\mathrm {L}} &=&L\frac {\mathrm {d}i_{2}}{\mathrm {d}t} \\[ 5pt ]
&=&L\frac {\mathrm {d}}{\mathrm {d}t}\left\{ \frac {R_{1}}{R_{1}+R_{2}}I\left( 1-\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t}\right) \right\} \\[ 5pt ]
&=&\frac {R_{1}LI}{R_{1}+R_{2}}\frac {\mathrm {d}}{\mathrm {d}t}\left( 1-\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t}\right) \\[ 5pt ]
&=&\frac {R_{1}LI}{R_{1}+R_{2}}\left( -\frac {R_{1}+R_{2}}{L}\right) \left( -\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t}\right) \\[ 5pt ]
&=&R_{1}I\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヘ
定常状態においては,リアクトル\( \ L \ \)は短絡と考えれば良いので,\( \ t=\infty \ \)における\( \ i_{1} \ \)は,分流の法則より,
\[
\begin{eqnarray}
i_{1} &=&\frac {R_{2}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ v_{\mathrm {R1}} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {R1}} &=&R_{1}i_{1} \\[ 5pt ]
&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは