《理論》〈電子理論〉[H23:問4]npnバイポーラトランジスタに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，$ \ \mathrm {npn} \ $バイポーラトランジスタに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も近いものを解答群の中から選びなさい。

平衡状態にある半導体の正孔濃度$ \ p \ $と電子濃度$ \ n \ $には$ \ pn \ $積一定という関係が成立する。この問題では$ \ p=n \ $の平衡状態では電子も正孔も真性キャリヤ濃度$ \ 1.4\times 10^{10} \ \mathrm {[cm^{-3}]} \ $の場合を考える。

そこで，不純物をドーピングすると多数キャリヤ濃度がドーピング濃度と等しいと近似できるので，$ \ p≠n \ $となる。しかし，$ \ pn \ $積一定の関係は維持されるので，多数キャリヤ濃度が決まると平衡時の少数キャリヤ濃度も決まる。

いま，ベースのドーピング濃度が$ \ 1.0\times 10^{18} \ \mathrm {[cm^{-3}]} \ $としよう。するとベースの少数キャリヤ濃度は$ \ \fbox {　（１）　} \ \mathrm {[cm^{-3}]} \ $となる。エミッタ・ベース間に電圧を印加しないときはベースの少数キャリヤ濃度はエミッタの多数キャリヤ濃度と拡散電位によって釣り合っている。ここで，ベース電位を零とし，エミッタ電位を負にすると，エミッタに隣接した場所でのベース内の少数キャリヤ濃度である電子濃度は，エミッタからの電子の注入により大きくなる。エミッタ電位が$ \ 60 \ \mathrm {[mV]} \ $負の方向に変化するごとにこの電子濃度が$ \ 10 \ $倍になる（$ \ 120 \ \mathrm {[mV]} \ $の変化では$ \ 100 \ $倍）とし，エミッタ電位を$ \ -780 \ \mathrm {[mV]} \ $とした場合，エミッタに隣接した場所でのベース内少数キャリヤ濃度は$ \ \fbox {　（２）　} \ \mathrm {[cm^{-3}]} \ $となる。

このとき，エミッタに隣接した場所では少数キャリヤ濃度は非平衡であり，ベース内での他の場所よりも少数キャリヤ濃度が高いことから電子は拡散してコレクタ側へ向かう。ベース中の再結合を無視できるとすると，電子の流れる量は濃度勾配の大きさ（単位長さ当たりの電子濃度の減少率）に拡散定数を掛けたものとなる。コレクタに隣接した場所ではベース内少数キャリヤ濃度が平衡時と等しいと考えると，これはエミッタに隣接した場所でのベース内少数キャリヤ濃度に比べて十分小さいので零と近似できる。ベース層の厚さを$ \ 1.0\times 10^{-5} \ \mathrm {[cm]} \ $とすると濃度勾配の大きさは$ \ \fbox {　（３）　} \ \mathrm {[cm^{-4}]} \ $となる。拡散係数が$ \ 25 \ \mathrm {[cm^{2}\cdot s^{-1}]} \ $であるとすると，電子の流れる量は$ \ \fbox {　（４）　} \ \mathrm {[cm^{-2}\cdot s^{-1}]} \ $となる。ベースから流れ出た電子の流れはコレクタ電流に相当するので，単位電荷$ \ 1.6\times 10^{-19} \ \mathrm {[C]} \ $を掛けるとコレクタ電流密度は$ \ \fbox {　（５）　} \ \mathrm {[A\cdot {cm}^{-2}]} \ $となる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　1.0\times 10^{2}　　　　&（ロ）&　2.0\times 10^{2}　　　　&（ハ）&　3.0\times 10^{2} \\[ 5pt ] &（ニ）&　5.0\times 10^{2}　　　　&（ホ）&　8.0\times 10^{2}　　　　&（ヘ）&　1.0\times 10^{10} \\[ 5pt ] &（ト）&　1.0\times 10^{15}　　　　&（チ）&　2.0\times 10^{15}　　　　&（リ）&　1.0\times 10^{16} \\[ 5pt ] &（ヌ）&　1.0\times 10^{20}　　　　&（ル）&　2.0\times 10^{20}　　　　&（ヲ）&　1.0\times 10^{21} \\[ 5pt ] &（ワ）&　3.0\times 10^{21}　　　　&（カ）&　5.0\times 10^{21}　　　　&（ヨ）&　1.0\times 10^{23} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {npn} \ $バイポーラトランジスタに関する問題です。
本問の内容を深堀りしていくと，エネルギーバンド構造等の専門性の強い分野となり，電験の範囲を超えることになります。
問題文にヒントが与えられるパターンの問題がほとんどなので，勉強効率を考え概要を理解する程度に留めるようにしましょう。

1.$ \ \mathrm {npn} \ $バイポーラトランジスタの構造と電圧印加時の概要
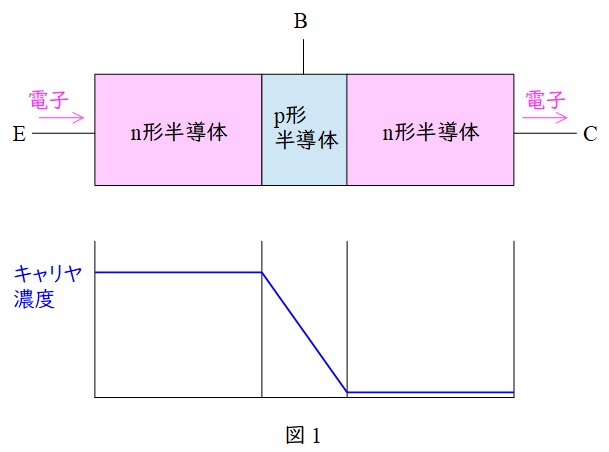
$ \ \mathrm {npn} \ $バイポーラトランジスタは，$ \ 2 \ $つの$ \ \mathrm {n} \ $形半導体の間に$ \ \mathrm {p} \ $形半導体を挟んだサンドイッチ構造となっています。
$ \ \mathrm {npn} \ $バイポーラトランジスタに$ \ V_{\mathrm {E}}＜V_{\mathrm {B}}＜V_{\mathrm {C}} \ $となる電圧をかけると，エミッタからは電子が供給され，コレクタからは電子が流れ出るので，ベース内の少数キャリヤ濃度（電子）はエミッタ側では高く，コレクタ側では低くなります。
このときのベース－エミッタ間電圧$ \ V_{\mathrm {BE}} \ $が大きくなると，ベースのエミッタ近傍のキャリヤ濃度$ \ n \ $は指数関数的に増加し，
\[
\begin{eqnarray}
n &∝&\mathrm {e}^{V_{\mathrm {BE}}}　\\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ロ
題意より，不純物ドーピング前後の$ \ pn \ $積は変わらないので，不純物のドーピング濃度が$ \ 1.0\times 10^{18} \ \mathrm {[cm^{-3}]} \ $のときのベースの少数キャリヤ濃度$ \ n_{\mathrm {B}} \ \mathrm {[cm^{-3}]} \ $は，
\[
\begin{eqnarray}
1.0\times 10^{18}\times n_{\mathrm {B}} &=&\left( 1.4\times 10^{10}\right) ^{2} \\[ 5pt ] n_{\mathrm {B}} &=&\frac {\left( 1.4\times 10^{10}\right) ^{2}}{1.0\times 10^{18}} \\[ 5pt ] &=&1.96\times 10^{2}　→　2.0\times 10^{2} \ \mathrm {[cm^{-3}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
ワンポイント解説「1.$ \ \mathrm {npn} \ $バイポーラトランジスタの構造と電圧印加時の概要」の通り，ベース内の少数キャリヤ濃度は指数関数的に増えていき，題意より$ \ 60 \ \mathrm {[mV]} \ $負の方向に変化するごとにこの電子濃度が$ \ 10 \ $倍（$ \ 120 \ \mathrm {[mV]} \ $の変化では$ \ 100 \ $倍）になるので，エミッタに隣接した場所での少数キャリヤ濃度$ \ n_{\mathrm {0}} \ \mathrm {[cm^{-3}]} \ $は，
\[
\begin{eqnarray}
n_{\mathrm {0}} &=&n_{\mathrm {B}}\times 10^{\frac {780}{60}} \\[ 5pt ] &=&2.0\times 10^{2}\times 10^{13} \\[ 5pt ] &=&2.0\times 10^{15} \ \mathrm {[cm^{-3}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
ワンポイント解説「1.$ \ \mathrm {npn} \ $バイポーラトランジスタの構造と電圧印加時の概要」及び題意の通り，コレクタ側のキャリヤ濃度は非常に低くほぼ零と近似でき，ベース層の厚さは$ \ W = 1.0\times 10^{-5} \ \mathrm {[cm]} \ $としているので，濃度勾配の大きさ$ \ \displaystyle \frac {\mathrm {d}n}{\mathrm {d}x} \ $は，
\[
\begin{eqnarray}
\frac {\mathrm {d}n}{\mathrm {d}x} &=&\frac {n_{\mathrm {0}}}{W} \\[ 5pt ] &=&\frac {2.0\times 10^{15}}{1.0\times 10^{-5}} \\[ 5pt ] &=&2.0\times 10^{20} \ \mathrm {[cm^{-4}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：カ
題意より，電子の流れる量$ \ N_{\mathrm {n}} \ \mathrm {[cm^{-2}\cdot s^{-1}]} \ $は，濃度勾配の大きさ$ \ \displaystyle \frac {\mathrm {d}n}{\mathrm {d}x} \ $に拡散定数$ \ D_{\mathrm {nB}}=25 \ \mathrm {[cm^{2}\cdot s^{-1}]} \ $を掛けたのであるから，
\[
\begin{eqnarray}
N_{\mathrm {n}} &=&\frac {\mathrm {d}n}{\mathrm {d}x}\cdot D_{\mathrm {nB}} \\[ 5pt ] &=&2.0\times 10^{20}\times 25 \\[ 5pt ] &=&5.0\times 10^{21} \ \mathrm {[cm^{-2}\cdot s^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
題意より，コレクタ電流密度$ \ J_{\mathrm {C}} \ \mathrm {[A\cdot {cm}^{-2}]} \ $は，電子の流れる量$ \ N_{\mathrm {n}} \ \mathrm {[cm^{-2}\cdot s^{-1}]} \ $に単位電荷$ \ e=1.6\times 10^{-19} \ \mathrm {[C]} \ $を掛けたものであるので，
\[
\begin{eqnarray}
J_{\mathrm {C}} &=&N_{\mathrm {n}}\cdot e \\[ 5pt ] &=&5.0\times 10^{21}\times 1.6\times 10^{-19} \\[ 5pt ] &=&8.0\times 10^{2} \ \mathrm {[A\cdot {cm}^{-2}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。