【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,抵抗の測定に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
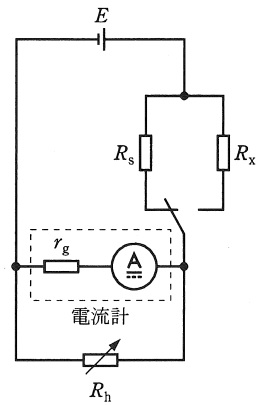
図の回路は既知の抵抗\( \ R_{\mathrm {s}} \ \)を標準として,未知の抵抗\( \ R_{\mathrm {x}} \ \)を測定するものである。図において,スイッチを\( \ R_{\mathrm {s}} \ \)側に倒し,可変抵抗\( \ R_{\mathrm {h}} \ \)を\( \ R_{\mathrm {h}}=R_{\mathrm {1}} \ \)に設定したところ電流計の読みが\( \ M_{\mathrm {1}} \ \)となった。次にスイッチを\( \ R_{\mathrm {x}} \ \)側に倒し,電流計の読みが\( \ M_{\mathrm {1}} \ \)になるように可変抵抗\( \ R_{\mathrm {h}} \ \)を調整したところ,\( \ R_{\mathrm {h}}=R_{\mathrm {2}} \ \)となった。ただし,電流計の内部抵抗を\( \ r_{\mathrm {g}} \ \)とし,直流電圧源\( \ E \ \)の内部抵抗は無視できるものとする。
いま,スイッチを\( \ R_{\mathrm {s}} \ \)及び\( \ R_{\mathrm {x}} \ \)側に倒したときの電流計に流れる電流を\( \ I_{\mathrm {s}} \ \)及び\( \ I_{\mathrm {x}} \ \)とすれば,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=& \ \fbox { (1) } \ &・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
I_{\mathrm {x}}&=& \ \fbox { (2) } \ &・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となる。電流計の読みが等しいので,①及び②式より\( \ R_{\mathrm {x}} \ \)は\( \ \fbox { (3) } \ \)となる。
次に,\( \ R_{\mathrm {x}} \ \)が既知,\( \ r_{\mathrm {g}} \ \)が未知の場合に対して,上記と同じ測定を行い\( \ r_{\mathrm {g}} \ \)を求めることを考える。電流計の読みが等しい場合には,①及び②式より\( \ r_{\mathrm {g}} \ \)は\( \ \fbox { (4) } \ \)となる。ここで,\( \ r_{\mathrm {g}}>0 \ \)であるので,電流計の読みが等しくなるように\( \ R_{\mathrm {h}} \ \)を調整すれば,測定に用いる\( \ R_{\mathrm {s}} \ \)と\( \ R_{\mathrm {x}} \ \)の抵抗値が\( \ R_{\mathrm {s}}>R_{\mathrm {x}} \ \)である場合には,\( \ R_{\mathrm {1}} \ \)と\( \ R_{\mathrm {2}} \ \)の大きさの関係は\( \ \fbox { (5) } \ \)となる。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{\mathrm {2}}R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) }{R_{\mathrm {1}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) } &(ロ)& \frac {R_{\mathrm {2}}r_{\mathrm {g}}}{R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) +R_{\mathrm {2}}r_{\mathrm {g}} }E \\[ 5pt ]
&(ハ)& R_{\mathrm {1}}<R_{\mathrm {2}} &(ニ)& \frac {r_{\mathrm {g}}}{R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}r_{\mathrm {g}} }E \\[ 5pt ]
&(ホ)& \frac {R_{\mathrm {2}}R_{\mathrm {s}}\left( R_{\mathrm {1}}-r_{\mathrm {g}}\right) }{R_{\mathrm {1}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) } &(ヘ)& \frac {R_{\mathrm {2}}}{R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) +R_{\mathrm {2}}r_{\mathrm {g}} }E \\[ 5pt ]
&(ト)& \frac {R_{\mathrm {1}}R_{\mathrm {2}}\left( R_{\mathrm {x}}-R_{\mathrm {s}}\right) }{R_{\mathrm {1}}R_{\mathrm {s}}-R_{\mathrm {2}}R_{\mathrm {x}}} &(チ)& \frac {R_{\mathrm {1}}}{R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}r_{\mathrm {g}} }E \\[ 5pt ]
&(リ)& \frac {R_{\mathrm {1}}r_{\mathrm {g}}}{R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}r_{\mathrm {g}} }E &(ヌ)& R_{\mathrm {1}}=R_{\mathrm {2}} \\[ 5pt ]
&(ル)& \frac {R_{\mathrm {1}}R_{\mathrm {2}}\left( R_{\mathrm {s}}-R_{\mathrm {x}}\right) }{R_{\mathrm {1}}R_{\mathrm {x}}-R_{\mathrm {2}}R_{\mathrm {s}}} &(ヲ)& \frac {R_{\mathrm {1}}R_{\mathrm {s}}r_{\mathrm {g}}}{R_{\mathrm {2}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) } \\[ 5pt ]
&(ワ)& \frac {R_{\mathrm {1}}R_{\mathrm {2}}\left( R_{\mathrm {s}}-R_{\mathrm {x}}\right) }{R_{\mathrm {2}}R_{\mathrm {x}}-R_{\mathrm {1}}R_{\mathrm {s}}} &(カ)& R_{\mathrm {1}}>R_{\mathrm {2}} \\[ 5pt ]
&(ヨ)& \frac {r_{\mathrm {g}}}{R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) +R_{\mathrm {2}}r_{\mathrm {g}} }E &&\\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
抵抗の測定に関する問題です。
式はやや長くなりますが,分流の法則や合成抵抗等の基本公式を理解していれば解ける問題なので,\( \ 2 \ \)種の受験生レベルを考えると正答率は高くなると思います。
1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時,それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。
①直列
直列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.分圧・分流の法則
①分圧の法則
図1に示した直列回路において,各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ]
V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ]
\end{eqnarray}
\]

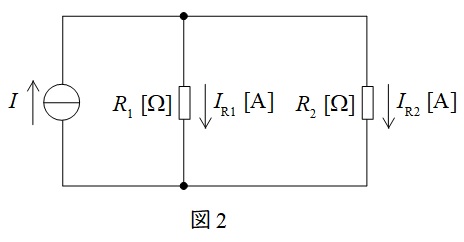
②分流の法則
図2に示した並列回路において,各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ]
I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:チ
スイッチを\( \ R_{\mathrm {s}} \ \)側に倒し,可変抵抗\( \ R_{\mathrm {h}} \ \)を\( \ R_{\mathrm {h}}=R_{\mathrm {1}} \ \)に設定したとき,回路の合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
R&=&R_{\mathrm {s}}+\frac {R_{\mathrm {1}}r_{\mathrm {g}}}{R_{\mathrm {1}}+r_{\mathrm {g}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,電源\( \ E \ \)を流れる電流\( \ I_{\mathrm {E}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {E}}&=&\frac {E}{R} \\[ 5pt ]
&=&\frac {E}{\displaystyle R_{\mathrm {s}}+\frac {R_{\mathrm {1}}r_{\mathrm {g}}}{R_{\mathrm {1}}+r_{\mathrm {g}}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。このとき,電流計に流れる電流\( \ I_{\mathrm {s}} \ \)は,分流の法則より,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {R_{\mathrm {1}}}{R_{\mathrm {1}}+r_{\mathrm {g}}}I_{\mathrm {E}} \\[ 5pt ]
&=&\frac {R_{\mathrm {1}}}{R_{\mathrm {1}}+r_{\mathrm {g}}}\cdot \frac {E}{\displaystyle R_{\mathrm {s}}+\frac {R_{\mathrm {1}}r_{\mathrm {g}}}{R_{\mathrm {1}}+r_{\mathrm {g}}}} \\[ 5pt ]
&=&\frac {R_{\mathrm {1}}}{R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}r_{\mathrm {g}}}E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヘ
(1)と同様に考えれば,\( \ R_{\mathrm {1}}→R_{\mathrm {2}} \ \),\( \ R_{\mathrm {s}}→R_{\mathrm {x}} \ \)とすれば良いので,
\[
\begin{eqnarray}
I_{\mathrm {x}}&=&\frac {R_{\mathrm {2}}}{R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) +R_{\mathrm {2}}r_{\mathrm {g}} }E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:イ
題意より,電流計の読みが等しい,すなわち\( \ I_{\mathrm {s}}=I_{\mathrm {x}} \ \)なので,
\[
\begin{eqnarray}
\frac {R_{\mathrm {1}}}{R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}r_{\mathrm {g}}}E&=&\frac {R_{\mathrm {2}}}{R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) +R_{\mathrm {2}}r_{\mathrm {g}} }E \\[ 5pt ]
\frac {R_{\mathrm {1}}}{R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}r_{\mathrm {g}}}&=&\frac {R_{\mathrm {2}}}{R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) +R_{\mathrm {2}}r_{\mathrm {g}} } \\[ 5pt ]
R_{\mathrm {1}}\left\{ R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) +R_{\mathrm {2}}r_{\mathrm {g}} \right\} &=&R_{\mathrm {2}}\left\{ R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}r_{\mathrm {g}}\right\} \\[ 5pt ]
R_{\mathrm {1}}R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}R_{\mathrm {2}}r_{\mathrm {g}} &=&R_{\mathrm {2}}R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) +R_{\mathrm {1}}R_{\mathrm {2}}r_{\mathrm {g}} \\[ 5pt ]
R_{\mathrm {1}}R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) &=&R_{\mathrm {2}}R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) \\[ 5pt ]
R_{\mathrm {x}}&=&\frac {R_{\mathrm {2}}R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) }{R_{\mathrm {1}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
\( \ R_{\mathrm {x}} \ \)が既知,\( \ r_{\mathrm {g}} \ \)が未知の場合,(3)と同様に求めれば,
\[
\begin{eqnarray}
R_{\mathrm {1}}R_{\mathrm {x}}\left( R_{\mathrm {2}}+r_{\mathrm {g}}\right) &=&R_{\mathrm {2}}R_{\mathrm {s}}\left( R_{\mathrm {1}}+r_{\mathrm {g}}\right) \\[ 5pt ]
R_{\mathrm {1}}R_{\mathrm {2}}R_{\mathrm {x}}+R_{\mathrm {1}}R_{\mathrm {x}}r_{\mathrm {g}} &=&R_{\mathrm {1}}R_{\mathrm {2}}R_{\mathrm {s}}+R_{\mathrm {2}}R_{\mathrm {s}}r_{\mathrm {g}} \\[ 5pt ]
R_{\mathrm {1}}R_{\mathrm {x}}r_{\mathrm {g}}-R_{\mathrm {2}}R_{\mathrm {s}}r_{\mathrm {g}} &=&R_{\mathrm {1}}R_{\mathrm {2}}R_{\mathrm {s}}-R_{\mathrm {1}}R_{\mathrm {2}}R_{\mathrm {x}} \\[ 5pt ]
\left( R_{\mathrm {1}}R_{\mathrm {x}}-R_{\mathrm {2}}R_{\mathrm {s}}\right) r_{\mathrm {g}} &=&R_{\mathrm {1}}R_{\mathrm {2}}\left( R_{\mathrm {s}}-R_{\mathrm {x}}\right) \\[ 5pt ]
r_{\mathrm {g}} &=&\frac {R_{\mathrm {1}}R_{\mathrm {2}}\left( R_{\mathrm {s}}-R_{\mathrm {x}}\right) }{R_{\mathrm {1}}R_{\mathrm {x}}-R_{\mathrm {2}}R_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
(4)解答式において,\( \ R_{\mathrm {s}}>R_{\mathrm {x}} \ \)ならば,分母も正である必要があるので,
\[
\begin{eqnarray}
R_{\mathrm {1}}R_{\mathrm {x}}-R_{\mathrm {2}}R_{\mathrm {s}} &>&0 \\[ 5pt ]
R_{\mathrm {1}}R_{\mathrm {x}}&>&R_{\mathrm {2}}R_{\mathrm {s}} \\[ 5pt ]
\frac {R_{\mathrm {1}}}{R_{\mathrm {2}}}&>&\frac {R_{\mathrm {s}}}{R_{\mathrm {x}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ R_{\mathrm {s}}>R_{\mathrm {x}} \ \)すなわち\( \ \displaystyle \frac {R_{\mathrm {s}}}{R_{\mathrm {x}}}>1 \ \)より,
\[
\begin{eqnarray}
\frac {R_{\mathrm {1}}}{R_{\mathrm {2}}}&>&\frac {R_{\mathrm {s}}}{R_{\mathrm {x}}}&>&1 \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ R_{\mathrm {1}}>R_{\mathrm {2}} \ \)と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは