《機械》〈回転機〉[H23:問1]三相誘導電動機の速度制御に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，三相誘導電動機の速度制御に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

三相誘導電動機の可変速制御方式として，三相電圧形$ \ \mathrm {PWM} \ $インバータを用いた$ \ V / f \ $制御が広く用いられている。誘導電動機の回転磁界の回転速度と回転子の回転速度はほぼ等しいので，回転磁界の回転速度を調節することによって，回転子のおおよその回転速度を制御することができる。

$ \ V / f \ $制御では，可変速制御を行う際に，目標とする回転子の回転速度が変化しても，一次電圧と$ \ \fbox {　（１）　} \ $との比率を一定に制御する。これによって，回転子の回転速度にかかわらず，回転磁界を発生するための$ \ \fbox {　（２）　} \ $の振幅をほぼ一定に保つことができる。このとき，二次巻線に誘導する起電力及び二次漏れリアクタンスは$ \ \fbox {　（３）　} \ $に比例する。その結果，回転磁界の回転速度が変化しても，トルクと$ \ \fbox {　（３）　} \ $との関係はほとんど変わらない。

実際の誘導電動機に$ \ V / f \ $制御を適用する場合，低速領域ではトルクの低下が生じる。これは，誘導電動機の$ \ \fbox {　（４）　} \ $による電圧降下に起因するものであり，この電圧降下の補償制御が必要になる場合もある。

また，高速領域では，インバータの出力電圧が飽和し，$ \ V / f \ $制御の比率を一定に制御できない場合がある。このような場合，一次電圧を一定にして回転子の回転速度を増加させる制御方法がある。一次電圧を一定としたとき，滑り周波数が一定であれば，誘導電動機のトルクは回転子の回転速度に対しておおよそ$ \ \fbox {　（５）　} \ $の関係となる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　回転子の回転速度　　　　　　　&（ロ）&　スイッチング周波数　　　　　　　&（ハ）&　一次電流 \\[ 5pt ] &（ニ）&　反比例　　　　　&（ホ）&　一次周波数　　　　　&（ヘ）&　二次巻線抵抗 \\[ 5pt ] &（ト）&　滑り周波数　　　　　&（チ）&　滑　り　　　　　&（リ）&　平方根に反比例 \\[ 5pt ] &（ヌ）&　励磁電流　　　　　&（ル）&　漏れインダクタンス　　　　　&（ヲ）&　二次電流 \\[ 5pt ] &（ワ）&　一次巻線抵抗　　　　　&（カ）&　キャリア周波数　　　　　&（ヨ）&　\ 2 \ 乗に反比例 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

三相誘導電動機のインバータ制御に関する問題です。
少し出題の仕方にひねりがある問題ですが，$ \ V / f \ $制御の概要は理解しておくようにしましょう。

1.三相誘導電動機の同期速度$ \ N_{\mathrm {s}} \ $
三相誘導電動機の極数が$ \ p \ $，電源の周波数が$ \ f \ $の時，同期速度$ \ N_{\mathrm {s}} \ $は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

2.誘導機の滑り$ \ s \ $
誘導機の同期速度が$ \ N_{\mathrm {s}} \ $，回転数が$ \ N \ $である時，誘導機の滑り$ \ s \ $は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.誘導電動機の$ \ \mathrm {L} \ $形等価回路
誘導電動機のL形等価回路は図1のようになります。図1において，$ \ {\dot V}_{1} \ $は一次側端子電圧，$ \ {\dot I}_{1} \ $は一次電流，$ \ {\dot I}_{2} \ $は二次電流，$ \ {\dot I}_{0} \ $は励磁電流，$ \ r_{1} \ $は一次巻線抵抗，$ \ r_{2}^{\prime } \ $は二次巻線抵抗の一次換算，$ \ x_{1} \ $は一次漏れリアクタンス，$ \ x_{2}^{\prime } \ $は二次漏れリアクタンスの一次換算，$ \ s \ $は滑りとなります。

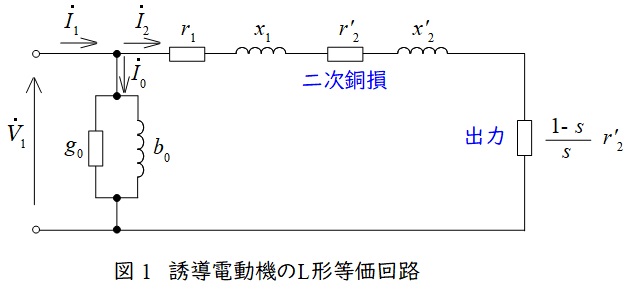
図1より，
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるから，二次入力$ \ P_{2} \ $は，
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ] &=&3\frac {r_{2}^{\prime}}{s}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right) ^{2} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\] となり，発生するトルク$ \ T \ $は，
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {(1-s)P_{2}}{(1-s)\omega _{s}} \\[ 5pt ] &=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

4.$ \ V / f \ $制御の概要
$ \ V / f \ $の値を一定に保つことで，磁気飽和が起こらないように磁束密度を一定として制御を行う方法です。
一次誘導起電力（相電圧）$ \ E_{1} \ $と一次周波数$ \ f \ $には，一次巻線係数$ \ K_{1} \ $，最大鎖交磁束$ \ \phi \ $，一次巻線の巻数$ \ N_{1} \ $とすると，
\[
\begin{eqnarray}
E_{1}&=&4.44K_{1}f\phi N_{1} \\[ 5pt ] \end{eqnarray}
\] の関係があり，$ \ \displaystyle \frac {E_{1}}{f} \ $を一定とすれば，$ \ \phi \ $は一定に保つことができるようになります。したがって$ \ V / f \ $制御では，電源の電圧と周波数の比を一定とさせます。

【解答】

(1)解答：ホ
題意より解答候補は，（ロ）スイッチング周波数，（ホ）一次周波数，（ト）滑り周波数，（カ）キャリア周波数，等になると思います。
ワンポイント解説「1.$ \ V / f \ $制御の概要」の通り，$ \ V / f \ $制御は一次電圧と一次周波数の比を一定にする制御となります。

(2)解答：ヌ
題意より解答候補は，（ハ）一次電流，（ヌ）励磁電流，（ヲ）二次電流，等になると思います。
ワンポイント解説「1.$ \ V / f \ $制御の概要」の通り，$ \ V / f \ $制御により磁束密度すなわち励磁電流（参考：電磁気の公式$ \ \mathit {\Phi }=BS=LI \ $）を一定にすることができます。

(3)解答：ト
題意より解答候補は，（イ）回転子の回転速度，（ト）滑り周波数，（チ）滑り，等になると思います。
誘導電動機の二次巻線に誘導する起電力$ \ E_{2}^{\prime } \ $は，二次巻線係数$ \ K_{1} \ $，二次周波数（滑り周波数）$ \ f_{2}=sf \ $，最大鎖交磁束$ \ \phi \ $，一次巻線の巻数$ \ N_{1} \ $とすると，
\[
\begin{eqnarray}
E_{2}^{\prime }&=&4.44K_{1}f_{2}\phi N_{1} \\[ 5pt ] &=&4.44K_{1}sf\phi N_{1} \\[ 5pt ] \end{eqnarray}
\] となり，二次漏れリアクタンス$ \ x_{2}^{\prime } \ $は，インダクタンスを$ \ L_{2} \ $とすると，
\[
\begin{eqnarray}
x_{2}^{\prime }&=&2\pi f_{2}L_{2} \\[ 5pt ] &=&2\pi sfL_{2} \\[ 5pt ] \end{eqnarray}
\] となります。また，トルクは，滑りにより変化するので，本問における選択肢は滑り周波数が適当となります。

(4)解答：ワ
題意より解答候補は，（ヘ）二次巻線抵抗，（ル）漏れインダクタンス，（ワ）一次巻線抵抗，になると思います。
ワンポイント解説「3.誘導電動機の$ \ \mathrm {L} \ $形等価回路」の通り，低速領域（滑り$ \ s \ $大）においては，一次巻線抵抗による電圧降下によるトルクの低下が大きくなります。

(5)解答：ヨ
題意より解答候補は，（ニ）反比例，（リ）平方根に反比例，（ヨ）$ \ 2 \ $乗に反比例，になると思います。
電源電圧が一定なので，鎖交磁束数は回転子の回転速度に反比例し，滑り周波数が一定であれば$ \ E_{2}^{\prime }=4.44K_{1}sf\phi N_{1} \ $より，二次電圧は鎖交磁束数に比例します。これにより，二次電流も二次電圧にほぼ比例しているので，二次電流は回転速度に反比例することになります。
トルクが出力に比例し二次電流の$ \ 2 \ $乗に比例することから，トルクは回転速度に対しておおよそ$ \ 2 \ $乗に反比例することになります。

※　導出はなかなか困難なので，覚えておいた方が良いかと思います。