《機械》〈変圧器〉[H27:問1]三脚鉄心を用いた三相リアクトルに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，三相リアクトルに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

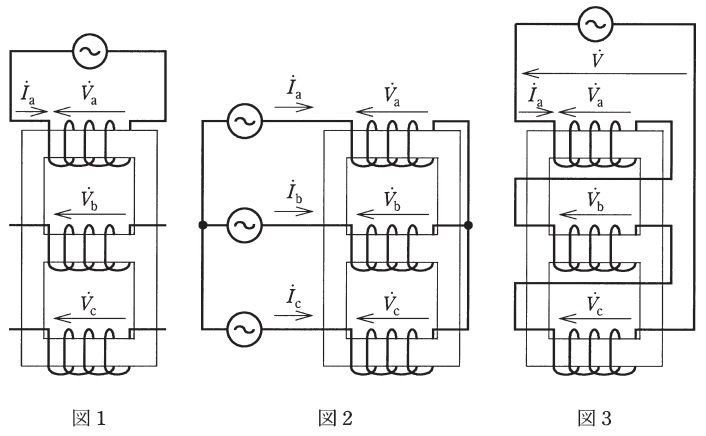
図1～図3は，三脚鉄心を用いた三相リアクトルである。鉄心の各脚(継鉄部を含む)の磁気抵抗は等しく線形とし，各相の巻線の巻数は等しく，巻線抵抗は無視できるものとする。図1のように$ \ \mathrm {a} \ $相の巻線にだけ角周波数$ \ \omega \ $の電流$ \ {\dot {I}}_{\mathrm {a}} \ $を流すと，$ \ \mathrm {a} \ $相の巻線には，
\[
{\dot {V}}_{\mathrm {a}}=\mathrm {j}\omega \left( L +L_{1}\right) {\dot {I}}_{\mathrm {a}}
\] の電圧が誘起する。ただし，$ \ L_{1} \ $は漏れインダクタンスであり，$ \ L+L_{1} \ $が自己インダクタンスとなる。$ \ \mathrm {b} \ $相及び$ \ \mathrm {c} \ $相の脚を通る磁束と$ \ \mathrm {a} \ $相の脚に生じる磁束との間の位相角は$ \ \fbox {　（１）　} \ $である。したがって，$ \ \mathrm {b} \ $相及び$ \ \mathrm {c} \ $相の巻線には，相互誘導によって，
\[
{\dot {V}}_{\mathrm {b}}={\dot {V}}_{\mathrm {c}}=-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {a}}
\] の電圧が誘起する。

図2のように，角周波数$ \ \omega \ $の三相電源を接続し，電流$ \ {\dot {I}}_{\mathrm {a}} \ $，$ \ {\dot {I}}_{\mathrm {b}} \ $及び$ \ {\dot {I}}_{\mathrm {c}} \ $を流した場合，$ \ \mathrm {a} \ $相の巻線には，
\[
{\dot {V}}_{\mathrm {a}}=\mathrm {j}\omega \left( L +L_{1}\right) {\dot {I}}_{\mathrm {a}}-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {b}}-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {c}}
\] の電圧が誘起する。$ \ {\dot {I}}_{\mathrm {a}} \ $，$ \ {\dot {I}}_{\mathrm {b}} \ $及び$ \ {\dot {I}}_{\mathrm {c}} \ $が対称三相交流電源であれば，
\[
\fbox {　（２）　}
\] であるので，$ \ \mathrm {a} \ $相の巻線の電圧は，
\[
{\dot {V}}_{\mathrm {a}}=\fbox {　（３）　}
\] となる。

図3のように，三相巻線を直列に接続して$ \ {\dot {I}}_{\mathrm {a}} \ $を流した場合，
\[
\dot {V}={\dot {V}}_{\mathrm {a}}+{\dot {V}}_{\mathrm {b}}+{\dot {V}}_{\mathrm {c}}=\fbox {　（４）　}
\] の電圧が誘起する。したがって，三脚鉄心を用いた三相リアクトルは，零相電流に対して$ \ \fbox {　（５）　} \ $となる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　{\dot {V}}_{\mathrm {a}}={\dot {V}}_{\mathrm {b}}={\dot {V}}_{\mathrm {c}}　　　&（ロ）&　高抵抗　　　&（ハ）&　\mathrm {j}\omega \left( \frac {1}{2}L+L_{1}\right) {\dot {I}}_{\mathrm {a}} \\[ 5pt ] &（ニ）&　高インピーダンス　　　&（ホ）&　90°　　　&（ヘ）&　{\dot {I}}_{\mathrm {a}}+{\dot {I}}_{\mathrm {b}}+{\dot {I}}_{\mathrm {c}}=0 \\[ 5pt ] &（ト）&　\mathrm {j}3\omega L_{1}{\dot {I}}_{\mathrm {a}}　　&（チ）&　120°　　　　&（リ）&　低インピーダンス \\[ 5pt ] &（ヌ）&　\mathrm {j}\omega \left( \frac {3}{2}L+L_{1}\right) {\dot {I}}_{\mathrm {a}}　　　&（ル）&　{\dot {I}}_{\mathrm {a}}={\dot {I}}_{\mathrm {b}}={\dot {I}}_{\mathrm {c}}　　　&（ヲ）&　\mathrm {j}\omega \left( -\frac {1}{2}L+L_{1}\right) {\dot {I}}_{\mathrm {a}} \\[ 5pt ] &（ワ）&　\mathrm {j}\omega L_{1}{\dot {I}}_{\mathrm {a}}　　　&（カ）&　180°　　　&（ヨ）&　\mathrm {j}3\omega \left( L+L_{1}\right) {\dot {I}}_{\mathrm {a}}
\end{eqnarray}
\]

【ワンポイント解説】

複雑な公式や定理を用いる問題ではなく，メカニズムを理解しているかどうかを問う非常に良い問題であると思います。

1.零相電圧，零相電流の定義
三相電圧$ \ {\dot {V}}_{\mathrm {a}} \ $，$ \ {\dot {V}}_{\mathrm {b}} \ $，$ \ {\dot {V}}_{\mathrm {c}} \ $及び三相電流$ \ {\dot {I}}_{\mathrm {a}} \ $，$ \ {\dot {I}}_{\mathrm {b}} \ $，$ \ {\dot {I}}_{\mathrm {c}} \ $が与えられている時，零相電圧$ \ {\dot {V}}_{0} \ $及び零相電流$ \ {\dot {I}}_{0} \ $は，
\[
\begin{eqnarray}
{\dot {V}}_{0}&=&\frac {1}{3}\left( {\dot {V}}_{\mathrm {a}}+{\dot {V}}_{\mathrm {b}}+{\dot {V}}_{\mathrm {c}}\right) \\[ 5pt ] {\dot {I}}_{0}&=&\frac {1}{3}\left( {\dot {I}}_{\mathrm {a}}+{\dot {I}}_{\mathrm {b}}+{\dot {I}}_{\mathrm {c}}\right) \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

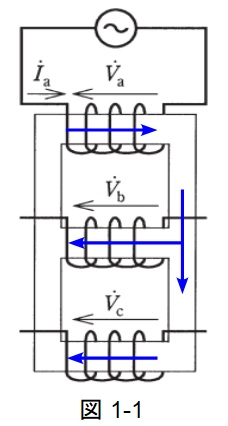
(1)解答：カ
図1-1の通り，$ \ \mathrm {a} \ $相の脚に生じた磁束は磁気回路を通り，$ \ \mathrm {b} \ $相，$ \ \mathrm {c} \ $相では磁束は反転します。よって，位相角は$ \ 180° \ $となります。

(2)解答：ヘ
対称三相交流である時，$ \ {\dot {I}}_{\mathrm {a}} \ $，$ \ {\dot {I}}_{\mathrm {b}} \ $及び$ \ {\dot {I}}_{\mathrm {c}} \ $の位相角はそれぞれ$ \ 120° \ $であり，大きさは等しいので，合計は零となります。よって，
\[
{\dot {I}}_{\mathrm {a}}+{\dot {I}}_{\mathrm {b}}+{\dot {I}}_{\mathrm {c}}=0
\] となります。

(3)解答：ヌ
\[
\begin{eqnarray}
{\dot {I}}_{\mathrm {a}}+{\dot {I}}_{\mathrm {b}}+{\dot {I}}_{\mathrm {c}}&=&0 \\[ 5pt ] {\dot {I}}_{\mathrm {a}}&=&-{\dot {I}}_{\mathrm {b}}-{\dot {I}}_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] を利用して$ \ {\dot {V}}_{\mathrm {a}} \ $の式を整理すると，
\[
\begin{eqnarray}
{\dot {V}}_{\mathrm {a}}&=&\mathrm {j}\omega \left( L +L_{1}\right) {\dot {I}}_{\mathrm {a}}-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {b}}-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {c}} \\[ 5pt ] &=&\mathrm {j}\omega \left( L +L_{1}\right) {\dot {I}}_{\mathrm {a}}+\mathrm {j}\omega \frac {L}{2}\left( -{\dot {I}}_{\mathrm {b}}-{\dot {I}}_{\mathrm {c}}\right) \\[ 5pt ] &=&\mathrm {j}\omega \left( L +L_{1}\right) {\dot {I}}_{\mathrm {a}}+\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {a}} \\[ 5pt ] &=&\mathrm {j}\omega \left( \frac {3}{2}L +L_{1}\right) {\dot {I}}_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ト
$ \ {\dot {I}}_{\mathrm {a}}={\dot {I}}_{\mathrm {b}}={\dot {I}}_{\mathrm {c}} \ $であるから，$ \ {\dot {V}}_{\mathrm {a}}={\dot {V}}_{\mathrm {b}}={\dot {V}}_{\mathrm {c}} \ $であり，
\[
\begin{eqnarray}
{\dot {V}}_{\mathrm {a}}&=&\mathrm {j}\omega \left( L +L_{1}\right) {\dot {I}}_{\mathrm {a}}-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {b}}-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {c}} \\[ 5pt ] &=&\mathrm {j}\omega \left( L +L_{1}\right) {\dot {I}}_{\mathrm {a}}-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {a}}-\mathrm {j}\omega \frac {L}{2}{\dot {I}}_{\mathrm {a}} \\[ 5pt ] &=&\mathrm {j}\omega L_{1}{\dot {I}}_{\mathrm {a}}
\end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
{\dot {V}}_{\mathrm {a}}+{\dot {V}}_{\mathrm {b}}+{\dot {V}}_{\mathrm {c}}&=&3{\dot {V}}_{\mathrm {a}} \\[ 5pt ] &=&\mathrm {j}3\omega L_{1}{\dot {I}}_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：リ
ワンポイント解説「1.零相電圧，零相電流の定義」より，零相電流$ \ {\dot {I}}_{0} \ $は，
\[
\begin{eqnarray}
{\dot {I}}_{0}&=&\frac {1}{3}\left( {\dot {I}}_{\mathrm {a}}+{\dot {I}}_{\mathrm {b}}+{\dot {I}}_{\mathrm {c}}\right) \\[ 5pt ] &=&\frac {1}{3}\left( {\dot {I}}_{\mathrm {a}}+{\dot {I}}_{\mathrm {a}}+{\dot {I}}_{\mathrm {a}}\right) \\[ 5pt ] &=&{\dot {I}}_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となる。一方零相電圧$ \ {\dot {V}}_{0} \ $は，
\[
\begin{eqnarray}
{\dot {V}}_{0}&=&\frac {1}{3}\left( {\dot {V}}_{\mathrm {a}}+{\dot {V}}_{\mathrm {b}}+{\dot {V}}_{\mathrm {c}}\right) \\[ 5pt ] &=&\frac {1}{3}\left( {\dot {V}}_{\mathrm {a}}+{\dot {V}}_{\mathrm {a}}+{\dot {V}}_{\mathrm {a}}\right) \\[ 5pt ] &=&{\dot {V}}_{\mathrm {a}} \\[ 5pt ] &=&\mathrm {j}\omega L_{1}{\dot {I}}_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となるので，零相インピーダンス$ \ Z_{0} \ $は，
\[
\begin{eqnarray}
Z_{0}&=&\left| \frac {{\dot {V}}_{0}}{{\dot {I}}_{0}}\right| \\[ 5pt ] &=&\left| \frac {\mathrm {j}\omega L_{1}{\dot {I}}_{\mathrm {a}}}{{\dot {I}}_{a}}\right| \\[ 5pt ] &=&\omega L_{1} \\[ 5pt ] \end{eqnarray}
\] となる。一般に$ \ L_{1} \ $は$ \ L \ $に比べて十分に小さいので，三脚鉄心を用いた三相リアクトルは，零相電流に対して低インピーダンスとなる。