《電力》〈水力〉[H24:問5]調整池式水力発電所の運用に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，調整池式水力発電所の運用に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。

調整池をもつ発電所では，河川流量が発電所の\( \ \fbox {　 （１） 　} \ \)より少ない場合，発電機は定格出力での連続運転ができず，一定の時間帯は発電機を\( \ \fbox {　 （２） 　} \ \)するか，出力を抑制して，定格出力で運転開始するまで調整池水位を\( \ \fbox {　 （３） 　} \ \)とするなど，必要な貯水量を確保する必要がある。

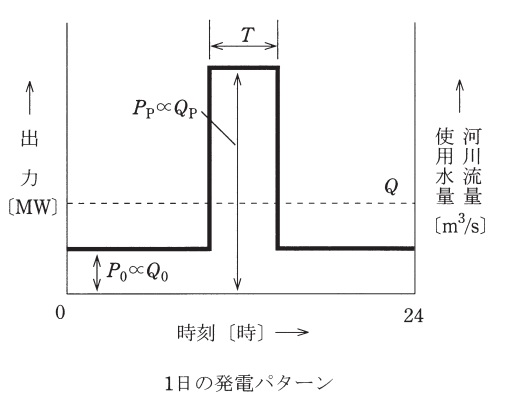
いま，河川の全流量を発電に利用し，毎日\( \ 0 \ \)時時点での貯水量を同じにする条件で，図のような１日の発電パターンで調整池式水力発電所を運転するものとする。また，発電機出力\( \ P_{0} \ \mathrm {[MW]} \ \)，\( \ P_{\mathrm {P}} \ \mathrm {[MW]} \ \)に対応する各使用水量を\( \ Q_{0} \ \mathrm {[m^{3}/s]} \ \)，\( \ Q_{\mathrm {P}} \ \mathrm {[m^{3}/s]} \ \)，\( \ P_{\mathrm {P}} \ \mathrm {[MW]} \ \)での運転継続時間を\( \ T \ \mathrm {[h]} \ \)とし，河川流量が\( \ Q \ \mathrm {[m^{3}/s]} \ \)で一定（ただし，\( \ Q_{0} \ ＜ \ Q \ ＜ \ Q_{\mathrm {P}} \ \))とすると，最低限必要な調整池の貯水容量\( \ V \ \mathrm {[m^{3}]} \ \)は，\( \ V= \ \fbox {　 （４） 　} \ \)で表される。このとき\( \ Q_{0} \ \mathrm {[m^{3}/s]} \ \)は\( \ Q_{0}=\fbox {　 （５） 　} \ \)で表される。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　QT\times \frac {P_{\mathrm {P}}}{P_{0}}\times 3600　　　　　&（ロ）&　最　低　　　　　&（ハ）&　Q_{\mathrm {P}}T\times 3600 \\[ 5pt ] &（ニ）&　下　限　　　　　&（ホ）&　\frac {Q\times \left( P_{\mathrm {P}}-P_{0}\right) }{P_{0}}　　　　　&（ヘ）&　豊水時流量 \\[ 5pt ] &（ト）&　満水位　　　　　&（チ）&　\left( Q_{\mathrm {P}}-Q\right) T\times 3600　　　　　&（リ）&　遅相運転 \\[ 5pt ] &（ヌ）&　進相運転　　　　　&（ル）&　無効放流量　　　　　&（ヲ）&　停　止 \\[ 5pt ] &（ワ）&　最大使用水量　　　　　&（カ）&　Q-\frac {V}{\left( 24-T\right) \times 3600}　　　　　&（ヨ）&　Q-\frac {V}{T \times 3600} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

水力発電所の運用に関する問題で，二次試験では定番の問題となります。３種の頃には出題が少ない，文章を読解させその場で考えさせる問題となっています。

1.水力発電所の出力
水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)は流量\( \ Q \ \mathrm {[m^{3}/s]} \ \)，有効落差\( \ H \ \mathrm {[m]} \ \)，水車及び発電機の総合効率を\( \ \eta \ \)とすると，
\[
\begin{eqnarray}
P&=&9.8QH\eta \\[ 5pt ] \end{eqnarray}
\] となります。したがって，出力\( \ P \ \mathrm {[kW]} \ \)は流量\( \ Q \ \mathrm {[m^{3}/s]} \ \)に比例することになります。

【解答】

(1)解答：ワ
題意より解答候補は，（ヘ）豊水時流量，（ル）無効放流量，（ワ）最大使用水量，になると思います。水力発電所が最大出力を出すときの水量を最大使用水量といい，これより河川流量が少ないと定格出力での連続運転ができなくなるので，負荷需要に合わせて出力を調整する必要があります。

(2)解答：ヲ
題意より解答候補は，（リ）遅相運転，（ヌ）進相運転，（ヲ）停止，になると思います。遅相運転や進相運転は無効電力の大きさを調整するのみなので，使用水量を抑えることができません。したがって，調整池の水位を上げるためには，停止するか出力抑制をするかになります。

(3)解答：ト
題意より解答候補は，（ロ）最低，（ニ）下限，（ト）満水位，になると思います。定格出力で運転すると，調整池の水位が下がっていくので，満水位としておくことが重要となります。

(4)解答：チ
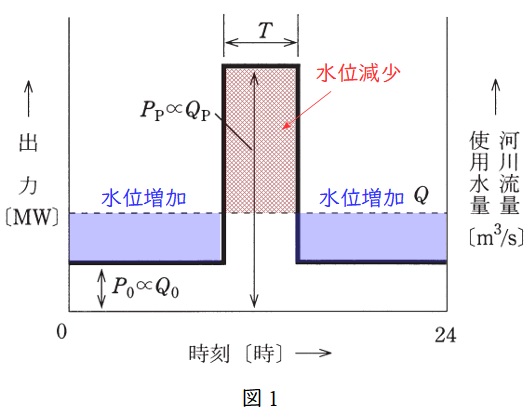
図1に示すように，発電機出力\( \ P_{\mathrm {P}} \ \mathrm {[MW]} \ \)の時は\( \ Q_{\mathrm {P}}-Q \ \mathrm {[m^{3}/s]} \ \)だけ調整池の水量が減少し，発電機出力\( \ P_{0} \ \mathrm {[MW]} \ \)の時は\( \ Q-Q_{0} \ \mathrm {[m^{3}/s]} \ \)だけ調整池の水量が増加することが分かる。
したがって，調整池は\( \ P_{\mathrm {P}} \ \mathrm {[MW]} \ \)で\( \ T \ \mathrm {[h]} \ \)運転した後に水位が下限になっても良いことがわかる。したがって，必要な貯水量\( \ V \ \mathrm {[m^{3}]} \ \)は，
\[
\begin{eqnarray}
V&=&\left( Q_{\mathrm {P}}-Q\right) \times 3600 \times T \\[ 5pt ] &=&\left( Q_{\mathrm {P}}-Q\right) T\times 3600 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：カ
\( \ P_{\mathrm {P}} \ \mathrm {[MW]} \ \)で\( \ T \ \mathrm {[h]} \ \)運転した後，\( \ P_{0} \ \mathrm {[MW]} \ \)で\( \ 24-T \ \mathrm {[h]} \ \)運転したときに満水になれば良いので，図１における水量増加量と水量減少量が等しくなればよい。したがって，
\[
\begin{eqnarray}
V&=&\left( Q-Q_{0}\right) \times 3600 \times \left( 24-T\right) \\[ 5pt ] \end{eqnarray}
\] となり，これを\( \ Q_{0} \ \)について整理すると，
\[
\begin{eqnarray}
V&=&\left( Q-Q_{0}\right) \times 3600\times \left( 24-T\right) \\[ 5pt ] Q-Q_{0} &=&\frac {V}{ \left( 24-T\right) \times 3600} \\[ 5pt ] Q_{0} &=&Q-\frac {V}{ \left( 24-T\right) \times 3600} \\[ 5pt ] \end{eqnarray}
\] と求められる。