《電力・管理》〈配電〉[H22:問4]誘導発電機を連系した高圧配電系統に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

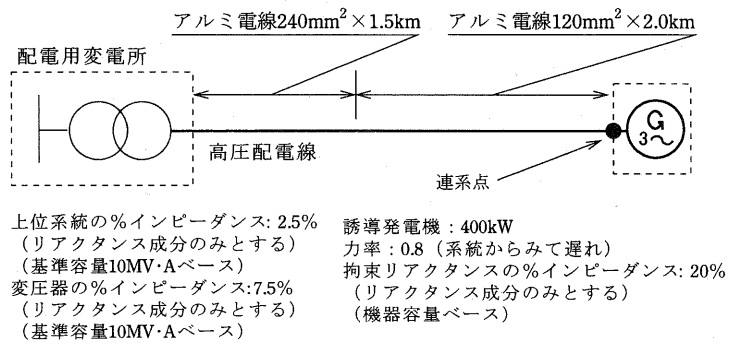
図のような高圧配電系統で，誘導発電機を連系した際，次の問に答えよ。ただし，基準容量\( \ 10 \ \mathrm {[MV\cdot A]} \ \)におけるアルミ電線\( \ 240 \ \mathrm {[{mm}^{2}]} \ \)の％インピーダンスは\( \ 1 \ \mathrm {[km]} \ \)当たり\( \ 2.9+\mathrm {j}7.1 \ \mathrm {[％／km]} \ \)，アルミ電線\( \ 120 \ \mathrm {[{mm}^{2}]} \ \)の％インピーダンスは\( \ 1 \ \mathrm {[km]} \ \)当たり\( \ 5.9+\mathrm {j}7.9 \ \mathrm {[％／km]} \ \)とする。

(1)　基準容量\( \ 10 \ \mathrm {[MV\cdot A]} \ \)において，配電系統との連系点からみた系統側の％インピーダンスを\( \ R_{0}+\mathrm {j}X_{0} \ \mathrm {[％]} \ \)とした場合，\( \ R_{0} \ \)，\( \ X_{0} \ \)の値をそれぞれ求めよ。

(2)　基準容量\( \ 10 \ \mathrm {[MV\cdot A]} \ \)において，誘導発電機の拘束インピーダンスはリアクタンス成分のみとし，これを\( \ X \ \mathrm {[％]} \ \)とした場合，\( \ X \ \)の値を求めよ。

(3)　誘導発電機の連系によって発生する，配電系統との連系点における瞬時電圧低下率を求めよ。なお，配電系統との連系点から誘導発電機端までのインピーダンス及び誘導発電機の抵抗成分は無視する。

【ワンポイント解説】

高圧配電系統に誘導発電機を接続した際の電圧降下率を求める問題です。
最後の(3)は少しだけ計算量が多いですが，(1)及び(2)に関しては比較的取り組みやすい内容なので，合格に向けては(1)と(2)をミスせずに確実に得点することが重要となります。

1.オーム法から百分率インピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンスの容量換算
「1.オーム法から百分率インピーダンス法への変換」の通り，百分率インピーダンスは基準容量に比例します。したがって，基準容量\( \ P_{\mathrm {A}} \ \mathrm {[V\cdot A]} \ \)から\( \ P_{\mathrm {B}} \ \mathrm {[V\cdot A]} \ \)へ変換する場合の百分率インピーダンスは，
\[
\begin{eqnarray}
％Z_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}％Z_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.負荷接続前後の電圧降下率
配電系統において，送電側の電圧を\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)一定，負荷接続前の負荷側の電圧を\( \ V_{\mathrm {r1}} \ \mathrm {[V]} \ \)，負荷接続後の負荷側の電圧を\( \ V_{\mathrm {r2}} \ \mathrm {[V]} \ \)としたとき，負荷接続後の電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&V_{\mathrm {s}}-V_{\mathrm {r2}} \\[ 5pt ] \end{eqnarray}
\] となり，電圧降下率\( \ ％\varepsilon \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％\varepsilon &=&\frac {\varepsilon }{V_{\mathrm {r1}}}\times 100 \\[ 5pt ] &=&\frac {V_{\mathrm {s}}-V_{\mathrm {r2}}}{V_{\mathrm {r1}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)基準容量\( \ 10 \ \mathrm {[MV\cdot A]} \ \)における配電系統との連系点からみた系統側の％インピーダンス
アルミ電線\( \ 240 \ \mathrm {[{mm}^{2}]} \ \)の％インピーダンス\( \ {\dot Z}_{1} \ \mathrm {[％]} \ \)及びアルミ電線\( \ 120 \ \mathrm {[{mm}^{2}]} \ \)の％インピーダンス\( \ {\dot Z}_{2} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
{\dot Z}_{1} &=&\left( 2.9+\mathrm {j}7.1 \right) \times 1.5 \\[ 5pt ] &=&4.35+\mathrm {j}10.65 \ \mathrm {[％]} \\[ 5pt ] {\dot Z}_{2} &=&\left( 5.9+\mathrm {j}7.9 \right) \times 2.0 \\[ 5pt ] &=&11.8+\mathrm {j}15.8 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] であり，上位系統の％インピーダンス\( \ {\dot Z}_{\mathrm {u}}=\mathrm {j}2.5 \ \mathrm {[％]} \ \)，変圧器の％インピーダンス\( \ {\dot Z}_{\mathrm {t}}=\mathrm {j}7.5 \ \mathrm {[％]} \ \)なので，配電系統との連系点からみた系統側の％インピーダンス\( \ R_{0}+\mathrm {j}X_{0} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
R_{0}+\mathrm {j}X_{0} &=&{\dot Z}_{\mathrm {u}}+{\dot Z}_{\mathrm {t}}+{\dot Z}_{1}+{\dot Z}_{2} \\[ 5pt ] &=&\mathrm {j}2.5+\mathrm {j}7.5+4.35+\mathrm {j}10.65+11.8+\mathrm {j}15.8 \\[ 5pt ] &=&16.15+\mathrm {j}36.45　→　16.2+\mathrm {j}36.5 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R_{0}=16.2 \ \mathrm {[％]} \ \)，\( \ X_{0}=36.5 \ \mathrm {[％]} \ \)と求められる。

(2)基準容量\( \ 10 \ \mathrm {[MV\cdot A]} \ \)における誘導発電機の拘束インピーダンス
誘導発電機の出力が\( \ 400 \ \mathrm {[kW]} \ \)，力率が\( \ 0.8 \ \)なので，機器容量\( \ P_{\mathrm {n}} \ \mathrm {[kV\cdot A]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {n}} &=&\frac {400}{0.8} \\[ 5pt ] &=&500 \ \mathrm {[kV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] である。これより，誘導発電機の拘束インピーダンスを\( \ 10 \ \mathrm {[MV\cdot A]} \ \)換算すると，ワンポイント解説「2.百分率インピーダンスの容量換算」の通り，
\[
\begin{eqnarray}
X &=&\frac {10\times 10^{3}}{P_{\mathrm {n}}}\times 20 \\[ 5pt ] &=&\frac {10\times 10^{3}}{500}\times 20 \\[ 5pt ] &=&400 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)誘導発電機の連系によって発生する，配電系統との連系点における瞬時電圧低下率
問題図において，上位系統の電圧を\( \ {\dot V}_{\mathrm {s}}=1.0 \ \mathrm {[p.u.]} \ \)，誘導発電機接続前の連系点の電圧を\( \ {\dot V}_{\mathrm {r1}} \ \mathrm {[p.u.]} \ \)，誘導発電機接続後の連系点の電圧を\( \ {\dot V}_{\mathrm {r2}} \ \mathrm {[p.u.]} \ \)とする。
(1)及び(2)より，単位法における配電系統との連系点からみた系統側のインピーダンス\( \ R_{0}+\mathrm {j}X_{0} \ \mathrm {[p.u.]} \ \)及び誘導発電機の拘束インピーダンス\( \ X \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
R_{0}+\mathrm {j}X_{0} &=&0.1615+\mathrm {j}0.3645 \ \mathrm {[p.u.]} \\[ 5pt ] X &=&4.0 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] である。
誘導発電機接続前は高圧配電線には電流が流れていないので，連系点の電圧\( \ {\dot V}_{\mathrm {r1}} \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {r1}} &=&{\dot V}_{\mathrm {s}} \\[ 5pt ] &=&1.0 \ \mathrm {[p.u.]}\\[ 5pt ] \end{eqnarray}
\] であり，誘導発電機接続後の連系点の電圧\( \ {\dot V}_{\mathrm {r2}} \ \mathrm {[p.u.]} \ \)は，分圧の法則より，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {r2}} &=&\frac {\mathrm {j}X}{R_{0}+\mathrm {j}X_{0}+\mathrm {j}X}{\dot V}_{\mathrm {s}} \\[ 5pt ] &=&\frac {\mathrm {j}4.0}{0.1615+\mathrm {j}0.3645+\mathrm {j}4.0}\times 1.0 \\[ 5pt ] &=&\frac {\mathrm {j}4.0}{0.1615+\mathrm {j}4.3645} \\[ 5pt ] \end{eqnarray}
\] となるので，その大きさ\( \ V_{\mathrm {r2}} \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {r2}} &=&\frac {4.0}{\sqrt {0.1615^{2}+4.3645^{2}}} \\[ 5pt ] &≒&0.91586 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，連系点における瞬時電圧低下率\( \ ％\varepsilon \ \mathrm {[％]} \ \)は，ワンポイント解説「3.負荷接続前後の電圧降下率」の通り，
\[
\begin{eqnarray}
％\varepsilon &=&\frac {V_{\mathrm {s}}-V_{\mathrm {r2}}}{V_{\mathrm {r1}}}\times 100 \\[ 5pt ] &=&\frac {1.0-0.91586}{1.0}\times 100 \\[ 5pt ] &≒&8.41 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。