《電力・管理》〈送電〉[R01:問2]単位法を使用した送電線の諸計算に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

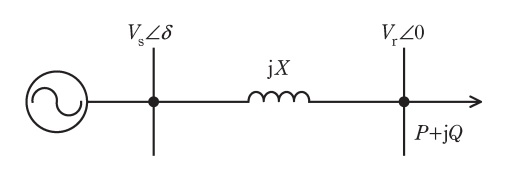
図に示すように，発電機より直列リアクタンス\( \ X \ \)をもつ送電線を介して負荷に有効電力\( \ P \ \)，無効電力\( \ Q \ \)を供給している場合を考える。ここに送電端電圧を\( \ V_{\mathrm {s}}∠\delta \ \)，受電端（負荷端）電圧を\( \ V_{\mathrm {r}}∠0 \ \)とする。また，無効電力の符号は遅れ無効電力を正とする。

(1)　負荷の有効電力\( \ P \ \)及び無効電力\( \ Q \ \)を，\( \ V_{\mathrm {s}} \ \)，\( \ V_{\mathrm {r}} \ \)，\( \ \delta \ \)及び\( \ X \ \)で表す式を導出せよ。

(2)　送電端電圧の大きさ\( \ V_{\mathrm {s}} \ \)を\( \ 1 \ \mathrm {p.u.} \ \)，送電線から負荷に供給する有効電力\( \ P \ \)を\( \ 0.5 \ \mathrm {p.u.} \ \)，無効電力\( \ Q \ \)を\( \ 0 \ \mathrm {p.u.} \ \)とするとき，受電端電圧の大きさ\( \ V_{\mathrm {r}} \ \)及び\( \ \delta \left( 0°≦\delta ≦45° \right) \ \)を求めたい。ここに送電線のリアクタンス\( \ X \ \)は\( \ 0.5 \ \mathrm {p.u.} \ \)とする。

a)　有効電力に関する式から\( \ V_{\mathrm {r}} \ \)を，\( \ \delta \ \)を用いて表せ。

b)　無効電力に関する式から\( \ V_{\mathrm {r}} \ \)を，\( \ \delta \ \)を用いて表せ。

c)　a)及びb)の結果から\( \ \delta \ \)及び\( \ V_{\mathrm {r}} \ \)の値を求めよ。

ただし，\( \sin 2x=2\sin x \cos x\)，\( \ \cos 2x=2\cos ^{2}x-1 \ \)を用いてもよい。

【ワンポイント解説】

送電線の送電端電圧及び受電端電圧から送電電力を計算する非常に出題されやすい問題です。（１）のように二次試験に関しては解答の式を暗記するのではなく，導出できるように普段から習熟しておくことが重要です。（２）に関しては半分は数学の問題です。

【解答】

(1)\( \ P \ \)及び\( \ Q \ \)を，\( \ V_{\mathrm {s}} \ \)，\( \ V_{\mathrm {r}} \ \)，\( \ \delta \ \)及び\( \ X \ \)で表す式
送電線の電流を\( \ \dot I \ \)とすると，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}&=&{\dot V}_{\mathrm {r}}+\mathrm {j}X\dot I \\[ 5pt ] \dot I&=&\frac {{\dot V}_{\mathrm {s}}-{\dot V}_{\mathrm {r}}}{\mathrm {j}X} \\[ 5pt ] \overline {\dot I}&=&\frac {\overline {{\dot V}_{\mathrm {s}}-{\dot V}_{\mathrm {r}}}}{-\mathrm {j}X} \\[ 5pt ] &=&\mathrm {j}\frac {V_{\mathrm {s}}∠\left( -\delta \right) -V_{\mathrm {r}}}{X} \\[ 5pt ] \end{eqnarray}
\] であり，遅れ無効電力を正とすると，負荷の送電電力から，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ] &=&V_{\mathrm {r}}\mathrm {j}\frac {V_{\mathrm {s}}∠\left( -\delta \right) -V_{\mathrm {r}}}{X} \\[ 5pt ] &=&V_{\mathrm {r}}\mathrm {j}\frac {V_{\mathrm {s}}\left( \cos \delta -\mathrm {j} \sin \delta \right) -V_{\mathrm {r}}}{X} \\[ 5pt ] &=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta +\mathrm {j}\frac {V_{\mathrm {s}}V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2}}{X} \\[ 5pt ] \end{eqnarray}
\] となり，両辺を比較すると，
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta \\[ 5pt ] Q&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2}}{X} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)a　有効電力に関する式から\( \ V_{\mathrm {r}} \ \)を，\( \ \delta \ \)を用いて表す
有効電力の式に各値を代入すると，
\[
\begin{eqnarray}
0.5&=&\frac {1\times V_{\mathrm {r}}}{0.5}\sin \delta \\[ 5pt ] V_{\mathrm {r}}&=&\frac {1}{4\sin \delta }\\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)b　無効電力に関する式から\( \ V_{\mathrm {r}} \ \)を，\( \ \delta \ \)を用いて表す
無効電力の式に各値を代入すると，
\[
\begin{eqnarray}
0&=&\frac {1\times V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2}}{0.5} \\[ 5pt ] 0&=&V_{\mathrm {r}}\cos \delta -V_{\mathrm {r}}^{2} \\[ 5pt ] V_{\mathrm {r}}^{2}&=&V_{\mathrm {r}}\cos \delta \\[ 5pt ] V_{\mathrm {r}}&=&\cos \delta \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)c　a)及びb)の結果から\( \ \delta \ \)及び\( \ V_{\mathrm {r}} \ \)を求める
a)及びb)の解答式から\( \ V_{\mathrm {r}} \ \)を消去すると，
\[
\begin{eqnarray}
\frac {1}{4\sin \delta }&=&\cos \delta \\[ 5pt ] 4\sin \delta \cos \delta &=&1\\[ 5pt ] 2\sin 2\delta &=&1\\[ 5pt ] \sin 2\delta &=&\frac {1}{2} \\[ 5pt ] 2\delta &=&\frac {\pi }{6} \\[ 5pt ] \delta &=&\frac {\pi }{12} \ \mathrm {[rad]} \\[ 5pt ] \end{eqnarray}
\] となり，これをb)の解答式に代入すると，
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&\cos \frac {\pi }{12} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ \displaystyle \cos 2x=2\cos ^{2}x-1 ⇔ \cos x= \sqrt {\frac {1+\cos 2x}{2}} \ \)の関係より，
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&\cos \frac {\pi }{12} \\[ 5pt ] &=&\sqrt {\frac {\displaystyle 1+\cos \frac {\pi }{6}}{2}} \\[ 5pt ] &≒&0.96593　→　0.966 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] と求められる。