《電力・管理》〈電気施設管理〉[H23:問6]送電線の送電電力の負荷率と損失係数に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

ある負荷に電力を供給している送電線の送電端電力のパターンが図のとおりであるとする（電力，時間は基準化してある）。この送電線の単位電力当たりの送電損失を\( \ R \ \)とするとき，次の問に答えなさい。

ただし，送電損失は抵抗分のみとし，送電端電圧，送電端力率は一定とする。

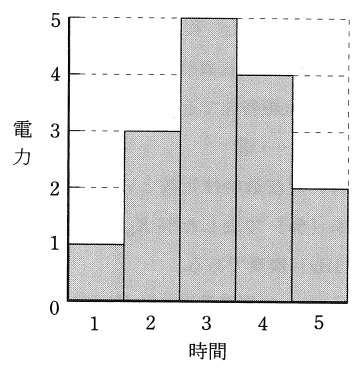
(1)　次の各値を求めよ。

　a.送電端負荷率

　b.損失係数

(2)　一般に，\( \ \mathrm {kWh} \ \)損失率（ある期間の送電損失率）と\( \ \mathrm {kW} \ \)損失率（その期間の最大電力時の送電損失率）の比は，損失係数と送電端負荷率の比に等しいことを示せ。

【ワンポイント解説】

電力の供給パターンから負荷率と損失係数を求める問題です。
負荷率は基本事項ですが，損失係数があまり電験では出題されない内容なので，損失係数を知っているかどうかがポイントとなります。
損失係数がわからない場合に(2)の証明問題をヒントとして，逆算から損失係数を導き出せるようになると，本番での対応力も高いレベルであると言えるでしょう。

1.需要率，不等率，負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②不等率（常に1以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {各最大需要電力の和}{合成した最大需要電力} \\[ 5pt ] \end{eqnarray}
\]

③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

2.損失係数，\( \ \mathrm {kW} \ \)損失率，\( \ \mathrm {kWh} \ \)損失率の定義
①損失係数
\[
\begin{eqnarray}
損失係数&=&\frac {平均損失電力}{最大損失電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②\( \ \mathrm {kW} \ \)損失率
\[
\begin{eqnarray}
\mathrm {kW} \ 損失率&=&\frac {最大損失電力}{最大電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

③\( \ \mathrm {kWh} \ \)損失率
\[
\begin{eqnarray}
\mathrm {kWh} \ 損失率&=&\frac {損失電力量}{送電電力量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)a.送電端負荷率
ワンポイント解説「1.需要率，不等率，負荷率の定義」より，送電端負荷率は，
\[
\begin{eqnarray}
送電端負荷率&=&\frac {平均送電電力}{最大送電電力}\times 100 \\[ 5pt ] &=&\frac {\displaystyle \frac {1\times 1 +3\times 1+5\times 1+4\times 1+2\times 1}{5}}{5}\times 100 \\[ 5pt ] &=&\frac {3}{5}\times 100 \\[ 5pt ] &=&60 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(1)b.損失係数
ワンポイント解説「2.損失係数，\( \ \mathrm {kW} \ \)損失率，\( \ \mathrm {kWh} \ \)損失率の定義」より，損失係数は，
\[
\begin{eqnarray}
損失係数&=&\frac {平均損失電力}{最大損失電力}\times 100 \\[ 5pt ] &=&\frac {\displaystyle \frac {\displaystyle R\times \left( \frac {1}{V}\right) ^{2}\times 1 +R\times \left( \frac {3}{V}\right) ^{2}\times 1+R\times \left( \frac {5}{V}\right) ^{2}\times 1+R\times \left( \frac {4}{V}\right) ^{2}\times 1+R\times \left( \frac {2}{V}\right) ^{2}\times 1}{5}}{\displaystyle R\times \left( \frac {5}{V}\right) ^{2}}\times 100 \\[ 5pt ] &=&\frac {\displaystyle \frac {11R}{V^{2}}}{\displaystyle \frac {25R}{V^{2}}}\times 100 \\[ 5pt ] &=&\frac {11}{25}\times 100 \\[ 5pt ] &=&44 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)\( \ \mathrm {kWh} \ \)損失率（ある期間の送電損失率）と\( \ \mathrm {kW} \ \)損失率（その期間の最大電力時の送電損失率）の比は，損失係数と送電端負荷率の比に等しいことを示す
ワンポイント解説「2.損失係数，\( \ \mathrm {kW} \ \)損失率，\( \ \mathrm {kWh} \ \)損失率の定義」より，
\[
\begin{eqnarray}
\frac { \ \mathrm {kWh} \ 損失率　　}{ \ \mathrm {kW} \ 損失率　　}&=&\frac {\displaystyle \frac {損失電力量}{送電電力量}\times 100}{\displaystyle \frac {最大損失電力}{最大送電電力}\times 100} \\[ 5pt ] &=&\frac {\displaystyle \frac {平均損失電力\times 時間}{平均送電電力\times 時間}\times 100}{\displaystyle \frac {最大損失電力}{最大送電電力}\times 100} \\[ 5pt ] &=&\frac {\displaystyle \frac {平均損失電力}{平均送電電力}\times 100}{\displaystyle \frac {最大損失電力}{最大送電電力}\times 100} \\[ 5pt ] &=&\frac {\displaystyle \frac {平均損失電力}{最大損失電力}\times 100}{\displaystyle \frac {平均送電電力}{最大送電電力}\times 100} \\[ 5pt ] &=&\frac {損失係数}{送電端負荷率} \\[ 5pt ] \end{eqnarray}
\] となるため，\( \ \mathrm {kWh} \ \)損失率（ある期間の送電損失率）と\( \ \mathrm {kW} \ \)損失率（その期間の最大電力時の送電損失率）の比は，損失係数と送電端負荷率の比に等しくなる。