《電力・管理》〈電気施設管理〉[H27:問5]変電所の設備容量に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

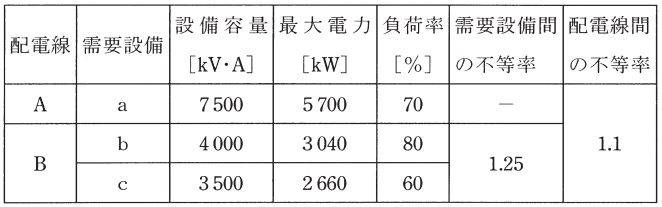
定格容量\( \ 9 \ 500 \ \mathrm {kV\cdot A} \ \)の変圧器\( \ 1 \ \)台を有する変電所から，配電線\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)により，下表に示す需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)に電力を供給しているとき，次の問に答えよ。

ただし，需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の需要率はそれぞれ\( \ 80 \ ％ \ \)，需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の負荷力率はそれぞれ遅れの一定値とし，結果は，小数第\( \ 1 \ \)位を四捨五入せよ。

(1)　需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の平均電力\( \ \mathrm {[kW]} \ \)をそれぞれ求めよ。

(2)　変電所の総合最大電力\( \ \mathrm {[kW]} \ \)を求めよ。

(3)　変電所の総合負荷率\( \ \mathrm {[％]} \ \)を求めよ。

(4)　需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の負荷力率\( \ \mathrm {[％]} \ \)をそれぞれ求めよ。

(5)　変圧器が過負荷とならないために必要なコンデンサの最小容量\( \ \mathrm {[kvar]} \ \)を求めよ。

【ワンポイント解説】

下記の公式を理解していれば比較的易しい問題となると思います。おそらくほとんどの受験者が選択されたのではないかと思います。ただし，前半で間違えてしまうとすべて間違いとなってしまうので，注意して計算をしましょう。

1.需要率
\[
需要率=\frac {最大需要電力}{設備容量}\times 100 \ [％] \]

2.負荷率
\[
負荷率=\frac {平均需要電力}{最大需要電力}\times 100 \ [％] \]

3.不等率
\[
不等率=\frac {各最大需要電力の和}{合成した最大需要電力}
\]

【解答】

(1)需要設備\(\mathrm {a}\)，\(\mathrm {b}\)，\(\mathrm {c}\)の平均電力\(\mathrm {[kW]}\)
需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の平均電力をそれぞれ\( \ \overline {P_{\mathrm {a}}} \ \)，\( \ \overline {P_{\mathrm {b}}} \ \)，\( \ \overline {P_{\mathrm {c}}} \ \)とすると，ワンポイント解説「2.負荷率」より，
\[
\begin{eqnarray}
\overline {P_{\mathrm {a}}} &=& 5 \ 700\times 0.7 \\[ 5pt ] &=& 3 \ 990 \ \mathrm {[kW]}\\[ 5pt ] \overline {P_{\mathrm {b}}} &=& 3 \ 040\times 0.8 \\[ 5pt ] &=& 2 \ 432 \ \mathrm {[kW]}\\[ 5pt ] \overline {P_{\mathrm {c}}} &=& 2 \ 660\times 0.6 \\[ 5pt ] &=& 1 \ 596 \ \mathrm {[kW]}\\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)変電所の総合最大電力\(\mathrm {[kW]}\)
需要設備\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の不等率が\( \ 1.25 \ \)であるから，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の合成した最大需要電力を\( \ P_{\mathrm {Bm}} \ \)とすると，ワンポイント解説「3.不等率」より，
\[
\begin{eqnarray}
P_{\mathrm {Bm}} &=& \frac{3 \ 040+2 \ 660}{1.25} \\[ 5pt ] &=& 4 \ 560 \ \mathrm {[kW]}\\[ 5pt ] \end{eqnarray}
\] となる。よって，変電所の総合最大電力\( \ P_{\mathrm {m}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {m}} &=& \frac{5 \ 700+4 \ 560}{1.1} \\[ 5pt ] &≒& 9 \ 327.3　→　9 \ 327 \ \mathrm {[kW]}\\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)変電所の総合負荷率\(\mathrm {[％]}\)
(1)，(2)より変電所の総合負荷率\( \ LF \ \)は，
\[
\begin{eqnarray}
LF &=& \frac{3 \ 990+2 \ 432+1 \ 596}{9 \ 327.3} \times 100 \\[ 5pt ] &≒& 85.963　→　86 \ \mathrm {[％]}\\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の負荷力率\(\mathrm {[％]}\)
需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の最大皮相電力\( \ S_{\mathrm {a}} \ \)，\( \ S_{\mathrm {b}} \ \)，\( \ S_{\mathrm {c}} \ \)とすると，ワンポイント解説「1.需要率」より，
\[
\begin{eqnarray}
S_{\mathrm {a}} &=& 7 \ 500\times 0.8 \\[ 5pt ] &=& 6 \ 000 \ \mathrm {[kV\cdot A]}\\[ 5pt ] S_{\mathrm {b}} &=& 4 \ 000\times 0.8 \\[ 5pt ] &=& 3 \ 200 \ \mathrm {[kV\cdot A]}\\[ 5pt ] S_{\mathrm {c}} &=& 3 \ 500\times 0.8 \\[ 5pt ] &=& 2 \ 800 \ \mathrm {[kV\cdot A]}\\[ 5pt ] \end{eqnarray}
\] となるので，それぞれの負荷力率\( \ \cos \theta _{\mathrm {a}} \ \)，\( \ \cos \theta _{\mathrm {b}} \ \)，\( \ \cos \theta _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\cos \theta _{\mathrm {a}} &=& \frac {5 \ 700}{6 \ 000} \\[ 5pt ] &=& 0.95　→　95 \ \mathrm {[％]}\\[ 5pt ] \cos \theta _{\mathrm {b}} &=& \frac {3 \ 040}{3 \ 200} \\[ 5pt ] &=& 0.95　→　95 \ \mathrm {[％]}\\[ 5pt ] \cos \theta _{\mathrm {c}} &=& \frac {2 \ 660}{2 \ 800} \\[ 5pt ] &=& 0.95　→　95 \ \mathrm {[％]}\\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)変圧器が過負荷とならないために必要なコンデンサの最小容量\(\mathrm {[kvar]}\)
需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の力率がすべて\( \ 0.95 \ \)であるから，その\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=& \sqrt{1-\cos ^{2}\theta} \\[ 5pt ] &=& \sqrt{1-0.95 ^{2}} \\[ 5pt ] &≒& 0.312 \ 25\\[ 5pt ] \end{eqnarray}
\] となる。これより，需要設備\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の最大無効電力を\( \ Q_{\mathrm {a}} \ \)，\( \ Q_{\mathrm {b}} \ \)，\( \ Q_{\mathrm {c}} \ \)とすると，
\[
\begin{eqnarray}
Q_{\mathrm {a}} &=& S_{\mathrm {a}}\sin \theta \\[ 5pt ] &=& 6 \ 000\times 0.312 \ 25 \\[ 5pt ] &=& 1 \ 873.5 \ \mathrm {[kvar]}\\[ 5pt ] Q_{\mathrm {b}} &=& S_{\mathrm {b}}\sin \theta \\[ 5pt ] &=& 3 \ 200\times 0.312 \ 25 \\[ 5pt ] &=& 999.2 \ \mathrm {[kvar]}\\[ 5pt ] Q_{\mathrm {c}} &=& S_{\mathrm {c}}\sin \theta \\[ 5pt ] &=& 2 \ 800\times 0.312 \ 25 \\[ 5pt ] &=& 874.3 \ \mathrm {[kvar]}\\[ 5pt ] \end{eqnarray}
\] となる。需要設備\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)の合成した最大無効電力を\( \ Q_{\mathrm {Bm}} \ \)とすると，
\[
\begin{eqnarray}
Q_{\mathrm {Bm}} &=& \frac{999.2+874.3}{1.25} \\[ 5pt ] &=& 1 \ 498.8 \ \mathrm {[kvar]}\\[ 5pt ] \end{eqnarray}
\] となるので，変電所の合成最大無効電力\( \ Q_{\mathrm {m}} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {m}} &=& \frac{1 \ 873.5+1 \ 498.8}{1.1} \\[ 5pt ] &≒& 3 \ 065.7 \ \mathrm {[kvar]}\\[ 5pt ] \end{eqnarray}
\] となる。よって，コンデンサ容量を\( \ Q_{\mathrm {C}} \ \)とすると，すべての合成容量が変電所の定格容量\( \ 9 \ 500 \ \mathrm {kV\cdot A} \ \)を下回れば良いので，
\[
\begin{eqnarray}
\sqrt {P_{\mathrm {m}}^{2}+\left( Q_{\mathrm {m}}-Q_{\mathrm {C}}\right)^{2}} &=& 9 \ 500 \\[ 5pt ] \sqrt {9 \ 327.3^{2}+\left( 3 \ 065.7-Q_{\mathrm {C}}\right)^{2}} &=& 9 \ 500 \\[ 5pt ] 9 \ 327.3^{2}+\left( 3 \ 065.7-Q_{\mathrm {C}}\right)^{2} &=& 9 \ 500^{2} \\[ 5pt ] \left( 3 \ 065.7-Q_{\mathrm {C}}\right)^{2} &≒& 3 \ 251 \ 500 \\[ 5pt ] 3 \ 065.7-Q_{\mathrm {C}} &≒& 1 \ 803.2 \\[ 5pt ] Q_{\mathrm {C}} &=& 1 \ 262.5　→　1 \ 263 \ \mathrm {[kvar]}\\[ 5pt ] \end{eqnarray}
\] と求められる。