《電力・管理》〈送電〉[R01:問3]電力系統の過渡安定性に関する論説問題

【問題】

【難易度】★★☆☆☆（やや易しい）

電力系統の過渡安定性に関して，次の問に答えよ。

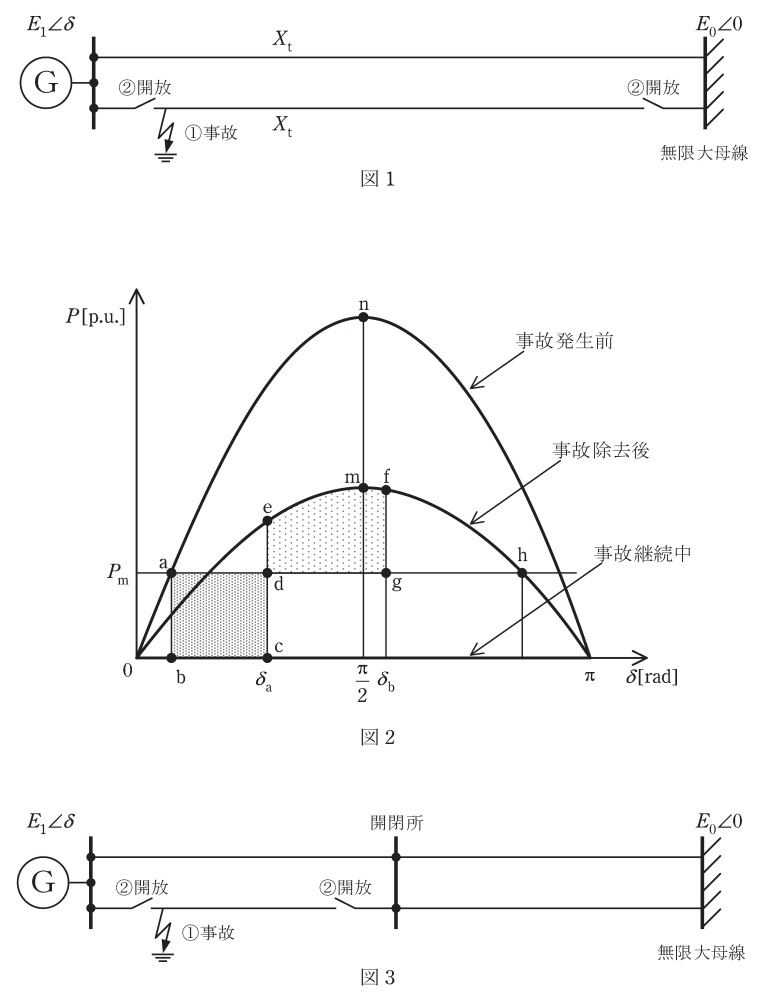
(1)　図1の\( \ 1 \ \)機無限大母線系統の過渡安定性について考える。発電機は，過渡リアクタンスを無視し，電圧\( \ E_{1}∠\delta \ \)で表され，送電線路は，\( \ 1 \ \)回線あたりのリアクタンスが\( \ X_{\mathrm {t}} \ \)の送電線が\( \ 2 \ \)回線併用されているものとする。また，発電機の機械的入力を\( \ P_{\mathrm {m}} \ \)，無限大母線の電圧を\( \ E_{0}∠0 \ \)とする。

送電端の至近で\( \ 1 \ \)回線三相地絡事故が発生し，同回線の両端の遮断器を開放することで事故を除去した場合を想定したとき，事故発生前，事故継続中，事故除去後の電力相差角曲線(\( \ P – \delta \ \)曲線)は図2のとおり表される。ここに，事故が除去されたときの\( \ \delta \ \)を\( \ \delta _{\mathrm {a}} \ \)とし，\( \ \delta \ \)はその後，\( \ \delta _{\mathrm {b}} \ \)まで至ったものとするとき，図2の面積\( \ \mathrm {abcd} \ \)と面積\( \ \mathrm {defg} \ \)のそれぞれについて，発電機の加速エネルギー又は減速エネルギーのどちらを表すか答えよ。

(2)　事故除去が遅れ，\( \ \delta _{\mathrm {a}} \ \)が大きくなった場合，過渡安定性を維持できる限界について，図2に記載されている記号を用いて簡潔に説明せよ。

(3)　図1の送電線路の中間点に開閉所を設置した図3の系統において，小問(1)と同じ事故が発生し，事故が発生した回線の両端の遮断器を開放することで事故を除去した場合を想定する。このとき，事故除去後の電力相差角曲線の電力の最大値は，開閉所の設置前の何倍になるか答えよ。

(4)　小問(3)の開閉所の設置により，過渡安定度が向上するか低下するかについて，加速エネルギーと減速エネルギーの変化に触れながら\( \ 200 \ \)字程度以内で説明せよ。

(5)　図3の系統において，送電線路の中間点にある開閉所に無効電力を高速に補償する装置を設置し，事故除去後，位相角\( \ \delta \ \)が最大値に至るまでの間，遅れ無効電力を系統側に注入した場合，小問(3)のときと比べ，位相角\( \ \delta \ \)の最大値はどう変化するか。加速エネルギーと減速エネルギーの変化に触れながら\( \ 200 \ \)字程度以内で説明せよ。

【ワンポイント解説】

過渡安定度のメカニズムに関する問題です。平成29年に等面積法について出題されていたので，その問題を理解されていたら解ける問題となります。令和元年度の２種合格者から最もお礼を言われた問題です。

1.等面積法
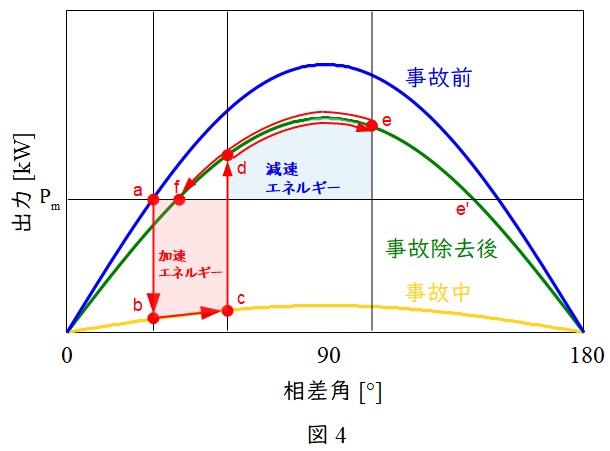
過渡安定度のメカニズムの説明には，送電電力\( \ P \ \)と相差角\( \ \delta \ \)の関係\( \ \left( \displaystyle P=\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{x}\sin \delta \right) \ \)を表す図4のような\( \ P-\delta \ \)曲線による等面積法が用いられます。
図4の\( \ \mathrm {a} \ \)で安定運転していた発電機が事故が発生すると，多量の無効電力が流れ，\( \ \mathrm {b} \ \)点に移動します。事故を除去する\( \ \mathrm {c} \ \)点まで発電機は加速し，事故除去後，線路は一相分なくなる分事故前よりリアクタンスが大きくなるため，\( \ P-\delta \ \)曲線は緑線になり，\( \ \mathrm {d} \ \)点に移動します。その後，発電機は減速エネルギーが働き始め，\( \ \mathrm {e} \ \)点まで進むと減速を開始し，元の出力と同じ\( \ \mathrm {f} \ \)点まで行くと発電機は安定します。減速エネルギーが足りず，\( \ \mathrm {e}^{\prime } \ \)点まで行ってしまうと脱調します。

【関連する「電気の神髄」記事】

　　一機無限大母線系統の過渡安定性と等面積法

【解答】

(1)図2の面積\( \ \mathrm {abcd} \ \)と面積\( \ \mathrm {defg} \ \)のそれぞれについて，発電機の加速エネルギー又は減速エネルギーのどちらを表すか
(ポイント)
・ワンポイント解説「1.等面積法」の通りです。

(試験センター解答)
面積\( \ \mathrm {abcd} \ \)：加速エネルギー
面積\( \ \mathrm {defg} \ \)：減速エネルギー

(2)事故除去が遅れ，\( \ \delta _{\mathrm {a}} \ \)が大きくなった場合，過渡安定性を維持できる限界について，図2に記載されている記号を用いて簡潔に説明
(ポイント)
・ワンポイント解説「1.等面積法」の通りです。

(試験センター解答例)
面積\( \ \mathrm {abcd} \ \)と面積\( \ \mathrm {deh} \ \)が等しくなる場合が過渡安定性を維持できる限界となる。

(3)図3の系統において，事故除去後の電力相差角曲線の電力の最大値は，開閉所の設置前の何倍になるか
(ポイント)
・\( \ P – \delta \ \)曲線において，電力\( \ P \ \)は，\( \ \displaystyle P=\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{x}\sin \delta \ \)で表されるので，リアクタンスに反比例する。
・開閉所設置前の\( \ 1 \ \)回線あたりのリアクタンスが\( \ X_{\mathrm {t}} \ \)であり，開閉所を設置することで事故除去後のリアクタンスが変化する。

(試験センター解答例)
電力相差角曲線の電力の最大値は，電源と無限大母線の間のリアクタンスに反比例する。開閉所設置前の事故除去後のリアクタンスは\( \ X_{\mathrm {t}} \ \)，開閉所設置後の事故除去後のリアクタンスは\( \ \displaystyle \frac {X_{\mathrm {t}}}{2}+\frac {X_{\mathrm {t}}}{2}÷2 =\frac {3X_{\mathrm {t}}}{4} \ \)であるから，電力相差角曲線の電力の最大値は\( \ \displaystyle \frac {4}{3} \ \)倍となる。

(4)小問(3)の開閉所の設置により，過渡安定度が向上するか低下するか
(ポイント)
・ワンポイント解説「1.等面積法」の事故除去後の線が上に上がるので，減速エネルギーが増加する。

(試験センター解答例)
加速エネルギーは開閉所設置前と変わらないが，事故除去後に位相角がある値に至るまでの減速エネルギーは開閉所設置前より増加することから，過渡安定性が向上する。

(5)開閉所に無効電力を高速に補償する装置を設置し，事故除去後，位相角\( \ \delta \ \)が最大値に至るまでの間，遅れ無効電力を系統側に注入した場合，小問(3)のときと比べ，位相角\( \ \delta \ \)の最大値はどう変化するか
(ポイント)
・遅れ無効電力を注入することで，系統の電圧が上昇する。
・系統の電圧が上昇すると，事故除去後の線が上に上がるので，減速エネルギーが増加する。

(試験センター解答例)
遅れの無効電力を系統側に注入することで，系統の電圧が上昇することから，事故除去後の電力相差角曲線が\( \ P \ \)軸の正方向に大きくなる。加速エネルギーは変わらないが，事故除去後に位相角がある値に至るまでの減速エネルギーは小問(3)のときより増加することから，位相角\( \ \delta \ \)の最大値は小さくなる。