Contents
【問題】
【難易度】★★★★☆(やや難しい)
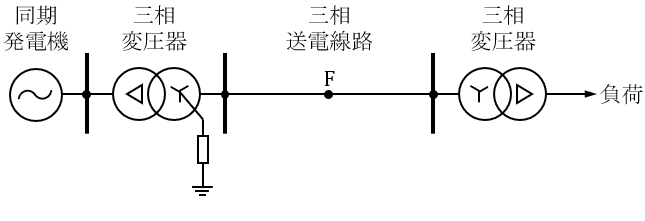
図の三相\( \ 3 \ \)線式\( \ 1 \ \)回線の送電線路において,中間地点である点\( \ \mathrm {F} \ \)で\( \ \mathrm {a} \ \)相の\( \ 1 \ \)線地絡故障が発生した場合を考える。三相変圧器はいずれも図のように\( \ \Delta -\mathrm {Y} \ \)結線であり,電源側では\( \ \mathrm {Y} \ \)結線の中性点が抵抗接地されており,負荷側では\( \ \mathrm {Y} \ \)結線の中性点は非接地である。三相変圧器,三相送電線路のインピーダンスはそれぞれ以下のとおりであり,点\( \ \mathrm {F} \ \)での地絡インピーダンスは零,負荷のインピーダンスは無限大とし,その他のインピーダンスは全て無視する。また,単位法の基準値は全て\( \ 154 \ \mathrm {kV} \ \)及び\( \ 1 \ 000 \ \mathrm {MV\cdot A} \ \)とする。
三相変圧器: 正相・逆相・零相漏れリアクタンス \( \ \mathrm {j} 0.2 \ \mathrm {p.u.} \ \)
電源側の変圧器の中性点接地抵抗 \( \ 15 \ \mathrm {p.u.} \ \)
三相送電線路:正相・逆相インピーダンス \( \ 0.01+\mathrm {j} 0.04 \ \mathrm {p.u.} \ \)
零相インピーダンス \( \ \mathrm {j} 0.2 \ \mathrm {p.u.} \ \)
点\( \ \mathrm {F} \ \)における故障発生前の線間電圧を\( \ 162 \ \mathrm {kV} \ \)として,次の問に答えよ。
(1) 点\( \ \mathrm {F} \ \)から系統を見た零相,正相,逆相インピーダンス\( \ \dot Z _{0} \ \mathrm {[p.u.]} \ \),\( \ \dot Z _{1} \ \mathrm {[p.u.]} \ \),\( \ \dot Z _{2} \ \mathrm {[p.u.]} \ \)を求めよ。
(2) 地絡電流\( \ \left| \dot I _{\mathrm {a}}\right| \ \mathrm {[p.u.]} \ \)を求めよ。ここで,点\( \ \mathrm {F} \ \)における故障発生前の\( \ \mathrm {a} \ \)相電圧を\( \ \dot E _{\mathrm {a}} \ \mathrm {[p.u.]} \ \)とすると,地絡電流の零相分\( \ \dot I _{0} \ \mathrm {[p.u.]} \ \)は次式で表される。
\[
\begin{eqnarray}
\dot I _{0}&=&\frac {\dot E _{\mathrm {a}}}{\dot Z _{0}+\dot Z _{1}+\dot Z _{2}} \\[ 5pt ]
\end{eqnarray}
\]
(3) 地絡電流の値\( \ \left| \dot I _{\mathrm {a}}\right| \ \mathrm {[A]} \ \)を求めよ。
【ワンポイント解説】
対称座標法を用いた\( \ 1 \ \)線地絡電流の導出に関する問題です。
計算量はそれほど多くありませんが,中性点接地抵抗の扱いを知らないと解けない問題です。
電験\( \ 1 \ \)種では比較的出題される内容ですが,\( \ 2 \ \)種での出題は少なく,受験生を惑わした問題かと思います。
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータとは,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
という関係があります。
2.対称座標法
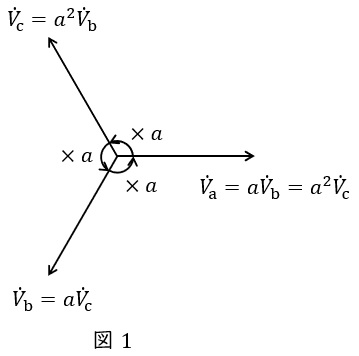
故障計算をする際に,非常に便利な方法で,零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)を用いて以下のように定義されます。ただし,\( \ a \ \)はベクトルオペレータとなります。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {0}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ {\dot V}_{\mathrm {b}} + {\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
{\dot V}_{\mathrm {1}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ a{\dot V}_{\mathrm {b}} + a^{2}{\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
{\dot V}_{\mathrm {2}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ a^{2}{\dot V}_{\mathrm {b}} + a{\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
\end{eqnarray}
\]
このとき,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
なお,図1に示すような三相平衡時においては,\( \ {\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}=0 \ \)であるため,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {0}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ {\dot V}_{\mathrm {b}} + {\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
&=&0 \\[ 5pt ]
{\dot V}_{\mathrm {1}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ a{\dot V}_{\mathrm {b}} + a^{2}{\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
&=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ {\dot V}_{\mathrm {a}} + {\dot V}_{\mathrm {a}}\right) \\[ 5pt ]
&=&{\dot V}_{\mathrm {a}} \\[ 5pt ]
{\dot V}_{\mathrm {2}} &=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ a^{2}{\dot V}_{\mathrm {b}} + a{\dot V}_{\mathrm {c}}\right) \\[ 5pt ]
&=&\frac {1}{3}\left( {\dot V}_{\mathrm {a}}+ {\dot V}_{\mathrm {c}} + {\dot V}_{\mathrm {b}}\right) \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となります。
同様に,零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)を用いて以下のように定義されます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {0}} &=&\frac {1}{3}\left( {\dot I}_{\mathrm {a}}+ {\dot I}_{\mathrm {b}} + {\dot I}_{\mathrm {c}}\right) \\[ 5pt ]
{\dot I}_{\mathrm {1}} &=&\frac {1}{3}\left( {\dot I}_{\mathrm {a}}+ a{\dot I}_{\mathrm {b}} + a^{2}{\dot I}_{\mathrm {c}}\right) \\[ 5pt ]
{\dot I}_{\mathrm {2}} &=&\frac {1}{3}\left( {\dot I}_{\mathrm {a}}+ a^{2}{\dot I}_{\mathrm {b}} + a{\dot I}_{\mathrm {c}}\right) \\[ 5pt ]
\end{eqnarray}
\]
このとき,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,対称座標法における零相インピーダンス\( \ {\dot Z}_{\mathrm {0}} \ \),正相インピーダンス\( \ {\dot Z}_{\mathrm {1}} \ \),逆相インピーダンス\( \ {\dot Z}_{\mathrm {2}} \ \),\( \ \mathrm {a} \ \)相の無負荷電圧\( \ {\dot E}_{\mathrm {a}} \ \)としたとき,発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-{\dot Z}_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-{\dot Z}_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-{\dot Z}_{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
これらの式を利用して,事故電流の大きさを求めます。
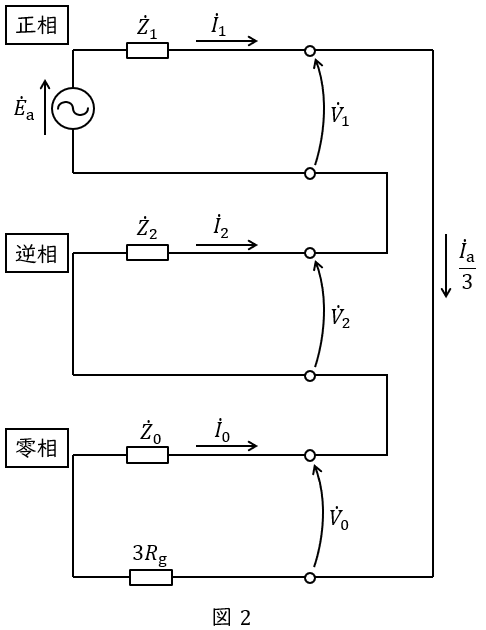
3.対称座標法による\( \ 1 \ \)線地絡故障時の等価回路
対称座標法を利用した\( \ \mathrm {a} \ \)相\( \ 1 \ \)線地絡故障時の等価回路は図2のようになります。ただし,\( \ R_{\mathrm {g}} \ \)は地絡抵抗となります。\( \ 1 \ \)線地絡故障時の対称座標法の関係式における\( \ \dot V_{\mathrm {a}}=0 \ \),\( \ \dot I_{\mathrm {b}}=\dot I_{\mathrm {c}}=0 \ \)及び発電機の基本式から導き出すことができますが,試験本番では覚えておく方が良いかと思います。
【解答】
(1)点\( \ \mathrm {F} \ \)から系統を見た零相,正相,逆相インピーダンス\( \ \dot Z _{0} \ \mathrm {[p.u.]} \ \),\( \ \dot Z _{1} \ \mathrm {[p.u.]} \ \),\( \ \dot Z _{2} \ \mathrm {[p.u.]} \ \)
中間地点\( \ \mathrm {F} \ \)から系統側を見た零相インピーダンス\( \ \dot Z _{0} \ \mathrm {[p.u.]} \ \)は,送電線の零相インピーダンスが中間地点なので\( \ \mathrm {j} 0.2 \ \mathrm {p.u.} \ \)の半分,ワンポイント解説「3.対称座標法による\( \ 1 \ \)線地絡故障時の等価回路」の通り中性点接地抵抗が\( \ 15 \ \mathrm {p.u.} \ \)の\( \ 3 \ \)倍であることに注意すると,
\[
\begin{eqnarray}
\dot Z _{0} &=&\frac {\mathrm {j} 0.2}{2}+\mathrm {j} 0.2+3\times 15 \\[ 5pt ]
&=&45+\mathrm {j} 0.3 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ、同様に,正相インピーダンス\( \ \dot Z _{1} \ \mathrm {[p.u.]} \ \)及び逆相インピーダンス\( \ \dot Z _{2} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\dot Z _{1} &=&\frac {0.01+\mathrm {j} 0.04}{2}+\mathrm {j} 0.2 \\[ 5pt ]
&=&0.005+\mathrm {j} 0.22 \ \mathrm {[p.u.]} \\[ 5pt ]
\dot Z _{2} &=&\frac {0.01+\mathrm {j} 0.04}{2}+\mathrm {j} 0.2 \\[ 5pt ]
&=&0.005+\mathrm {j} 0.22 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
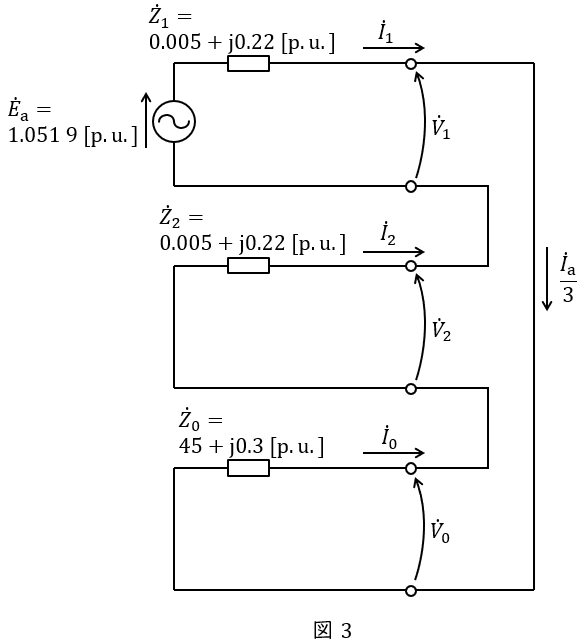
(2)地絡電流\( \ \left| \dot I _{\mathrm {a}}\right| \ \mathrm {[p.u.]} \ \)
点\( \ \mathrm {F} \ \)における故障発生前の電圧\( \ \dot E_{\mathrm {a}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\dot E_{\mathrm {a}} &=&\frac {162}{154} \\[ 5pt ]
&≒&1.051 \ 9 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ 1 \ \)線地絡時の等価回路は図3の通りとなる。図3より地絡電流\( \ \dot I _{\mathrm {a}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\frac {\dot I_{\mathrm {a}}}{3} &=&\frac {\dot E _{\mathrm {a}}}{\dot Z _{0}+\dot Z _{1}+\dot Z _{2}} \\[ 5pt ]
\dot I_{\mathrm {a}}&=&\frac {3\dot E _{\mathrm {a}}}{\dot Z _{0}+\dot Z _{1}+\dot Z _{2}} \\[ 5pt ]
&=&\frac {3\times 1.051 \ 9}{45+\mathrm {j} 0.3+0.005+\mathrm {j} 0.22+0.005+\mathrm {j} 0.22} \\[ 5pt ]
&=&\frac {3.155 \ 7}{45.010+\mathrm {j} 0.74} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさ\( \ \left| \dot I _{\mathrm {a}}\right| \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\left| \dot I _{\mathrm {a}}\right| &=&\frac {3.155 \ 7}{\sqrt {45.010^{2}+0.74^{2}}} \\[ 5pt ]
&≒&0.070 \ 102 → 0.070 \ 1 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)地絡電流の値\( \ \left| \dot I _{\mathrm {a}}\right| \ \mathrm {[A]} \ \)
基準電流\( \ I_{\mathrm {B}} \ \mathrm {[A]} \ \)は,基準電圧\( \ V_{\mathrm {B}}=154 \ \mathrm {[kV]} \ \)及び\( \ P_{\mathrm {B}}=1 \ 000 \ \mathrm {[MV\cdot A]} \ \)より,
\[
\begin{eqnarray}
I_{\mathrm {B}} &=&\frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {1 \ 000\times 10^{6}}{\sqrt {3}\times 154 \times 10^{3}} \\[ 5pt ]
&≒&3 \ 749.0 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,地絡電流\( \ \left| \dot I _{\mathrm {a}}\right| \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
\left| \dot I _{\mathrm {a}}\right| \ \mathrm {[A]} &=&I_{\mathrm {B}}\cdot \left| \dot I _{\mathrm {a}}\right| \ \mathrm {[p.u.]} \\[ 5pt ]
&=&3 \ 749.0 \times 0.0701 \ 02 \\[ 5pt ]
&≒&263 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは