《電力》〈送電〉[R04:問7]電力系統の過渡安定度の判別法の一つの等面積法に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，電力系統の過渡安定度の判別法の一つの等面積法に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

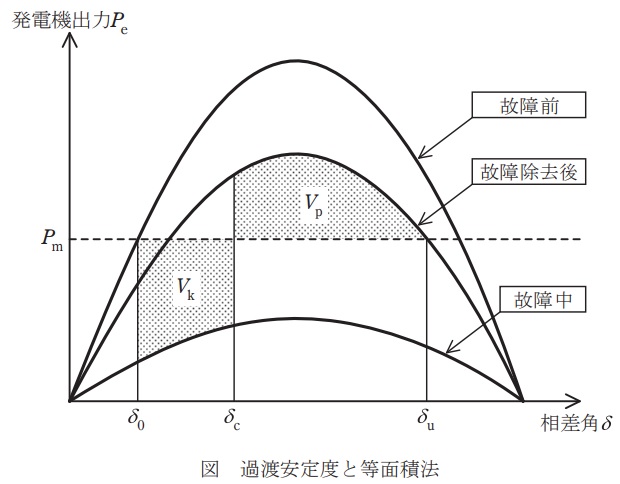
電力系統における過渡安定度の基本的な説明には，図の等面積法が多く用いられる。この図で，地絡等の故障中は発電機の機械入力$ \ P_{\mathrm {m}} \ $が電気出力$ \ P_{\mathrm {e}} \ $より大きいため，この発電機の$ \ \fbox {　（１）　} \ $し，相差角$ \ \delta \ $は$ \ \fbox {　（２）　} \ $。

次いで，一定時間後(相差角$ \ \delta _{\mathrm {c}} \ $)で故障が除去されると，以降，電気出力$ \ P_{\mathrm {e}} \ $が機械入力$ \ P_{\mathrm {m}} \ $を上回り，発電機の$ \ \fbox {　（３）　} \ $し始める。

この間も$ \ \delta \ $は増加するが，図の面積$ \ V _{\mathrm {k}}＜V _{\mathrm {p}} \ $であれば，$ \ \delta \ $が$ \ \delta _{\mathrm {u}} \ $に達する前にその最大値に達し，以降，$ \ \delta \ $はその最大値$ \ \fbox {　（４）　} \ $。すなわち，安定と判定される。

一方，$ \ V _{\mathrm {k}}＞V _{\mathrm {p}} \ $であれば$ \ \delta \ $は$ \ \delta _{\mathrm {u}} \ $を越え，以降，$ \ \delta \ $は増大して$ \ \fbox {　（５）　} \ $。この場合は，不安定(脱調)と判定される。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　回転数は振動　　　　　　　&（ロ）&　大きく振動する　　　　　　　&（ハ）&　180 \ 度まで進み止まる \\[ 5pt ] &（ニ）&　増大する　　　　　&（ホ）&　電流は振動　　　　　&（ヘ）&　回転数は減少 \\[ 5pt ] &（ト）&　乱調する　　　　　&（チ）&　から減少する　　　　　&（リ）&　電流は減少 \\[ 5pt ] &（ヌ）&　発散する　　　　　&（ル）&　電圧は振動　　　　　&（ヲ）&　脈動する \\[ 5pt ] &（ワ）&　回転数は増大　　　　　&（カ）&　に留まる　　　　　&（ヨ）&　から \ \delta _{\mathrm {c}} \ まで移行する \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

過渡安定度の判別に用いる等面積法に関する問題です。
等面積法は令和４年度は一次試験に出題されていますが，令和元年には二次試験で出題されています。
したがって，本問の内容は空欄穴埋レベルではなく，他の人に説明できるぐらいのレベルを目指すようにしましょう。

1.等面積法
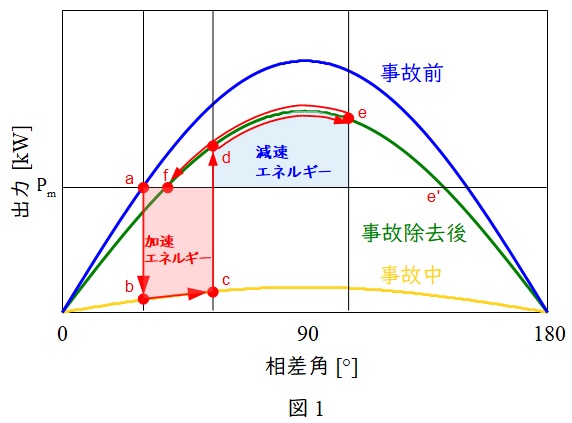
過渡安定度のメカニズムの説明には，送電電力$ \ P \ $と相差角$ \ \delta \ $の関係$ \ \left( \displaystyle P=\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{x}\sin \delta \right) \ $を表す図1のような$ \ P-\delta \ $曲線による等面積法が用いられます。
図1の$ \ \mathrm {a} \ $で安定運転していた発電機に事故が発生すると，多量の無効電力が流れ，$ \ \mathrm {b} \ $点に移動します。事故を除去する$ \ \mathrm {c} \ $点まで発電機は加速し，事故除去後，線路は一相分なくなる分事故前よりリアクタンスが大きくなるため，$ \ P-\delta \ $曲線は緑線になり，$ \ \mathrm {d} \ $点に移動します。その後，発電機は減速エネルギーが働き始め，$ \ \mathrm {e} \ $点まで進むと減速を開始し，元の出力と同じ$ \ \mathrm {f} \ $点まで行くと発電機は安定します。減速エネルギーが足りず，$ \ \mathrm {e}^{\prime } \ $点まで行ってしまうと脱調します。
したがって，加速エネルギーを大きくしないためには，超速応励磁方式を採用し$ \ \mathrm {b} \ $点から$ \ \mathrm {c} \ $点までの距離を短くすることが効果的となります。

【解答】

(1)解答：ワ
題意より解答候補は，（イ）回転数は振動，（ホ）電流は振動，（ヘ）回転数は減少，（リ）電流は減少，（ル）電圧は振動，（ワ）回転数は増大，になると思います。
ワンポイント解説「1.等面積法」の通り，故障中は発電機の機械入力$ \ P_{\mathrm {m}} \ $が電気出力$ \ P_{\mathrm {e}} \ $より大きくなり，発電機の回転数は増大します。自転車のチェーンが外れたようなイメージ（ガクンと加速するイメージ）をすると良いかと思います。

(2)解答：ニ
題意より解答候補は，（ロ）大きく振動する，（ハ）$ \ 180 \ $度まで進み止まる，（ニ）増大する，（ト）乱調する，（ヌ）発散する，（ヲ）脈動する，になると思います。
ワンポイント解説「1.等面積法」の通り，故障中は発電機の相差角は増大します。

(3)解答：ヘ
題意より解答候補は，（イ）回転数は振動，（ホ）電流は振動，（ヘ）回転数は減少，（リ）電流は減少，（ル）電圧は振動，（ワ）回転数は増大，になると思います。
ワンポイント解説「1.等面積法」の通り，故障が除去されると，電気出力$ \ P_{\mathrm {e}} \ $が機械入力$ \ P_{\mathrm {m}} \ $を上回り，発電機の回転数は減少し始めます。

(4)解答：チ
題意より解答候補は，（チ）から減少する，（カ）に留まる，（ヨ）から$ \ \delta _{\mathrm {c}} \ $まで移行する，になると思います。
ワンポイント解説「1.等面積法」の通り，$ \ V _{\mathrm {k}}＜V _{\mathrm {p}} \ $であれば，加速エネルギーよりも減速エネルギーの方が大きいので，$ \ \delta \ $はその最大値から減少することになります。

(5)解答：ヌ
題意より解答候補は，（ロ）大きく振動する，（ト）乱調する，（ヌ）発散する，（ヲ）脈動する，になると思います。
ワンポイント解説「1.等面積法」の通りですが，用語が少し気になる空欄です。減速エネルギーが加速エネルギーよりも小さいと，そのまま振動や脈動等を起こすことなく脱調してしまいます。したがって，最も適切なのは発散するとなります。