【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,電荷を帯びた球の作る電界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
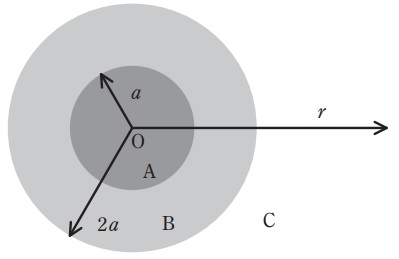
図のように,真空中の原点\( \ \mathrm {O} \ \)からの距離が\( \ r \ \)であるとき,\( \ 0≦r≦a \ \),\( \ a≦r≦2a \ \),\( \ r>2a \ \)の領域をそれぞれ領域\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)とする。領域\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)にはそれぞれ電荷密度\( \ +\rho \ \),\( \ \displaystyle -\frac {\rho }{7} \ \)で電荷が一様に分布している。また,領域\( \ \mathrm {C} \ \)に電荷は存在しない。ただし,\( \ \rho >0 \ \)であり,全ての領域の誘電率は真空中の誘電率\( \ \varepsilon _{0} \ \)である。
このとき,領域\( \ \mathrm {A} \ \)に存在する電荷の合計は\( \ \fbox { (1) } \ \)である。
また,球の中心から距離\( \ r \ \)の位置における\( \ r \ \)方向の電界\( \ E\left( r\right) \ \)は,
領域\( \ \mathrm {A}\left( 0≦r≦a\right) \ \)のとき\( \ \fbox { (2) } \ \)
領域\( \ \mathrm {B}\left( a≦r≦2a\right) \ \)のとき\( \ \fbox { (3) } \ \)
領域\( \ \mathrm {C}\left( r>2a\right) \ \)のとき\( \ \fbox { (4) } \ \)
である。
このとき,\( \ E\left( r\right) \ \)の符号に着目すると,\( \ r→\infty \ \)の無限遠点を電位の基準とした場合に,中心\( \ \mathrm {O}\left( r=0\right) \ \)の電位の符号は,\( \ \fbox { (5) } \ \)。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 4\pi a^{3}\rho &(ロ)& \frac {\rho }{3\varepsilon _{0}}\frac {a^{3}}{r^{2}} &(ハ)& \frac {\rho }{3\varepsilon _{0}}\frac {a^{2}}{r} \\[ 5pt ]
&(ニ)& \frac {\rho }{3\varepsilon _{0}}r &(ホ)& \frac {\rho }{21\varepsilon _{0}}\left( \frac {8a^{3}}{r^{2}}-r\right) &(ヘ)& \frac {8}{3}\pi a^{3}\rho \\[ 5pt ]
&(ト)& 負である &(チ)& \frac {\rho }{9\varepsilon _{0}}\left( \frac {4a^{3}}{r^{2}}-r\right) &(リ)& \frac {\rho }{21\varepsilon _{0}}\left( \frac {6a^{3}}{r^{2}}+r\right) \\[ 5pt ]
&(ヌ)& -\frac {\rho }{3\varepsilon _{0}}\frac {a^{2}}{r} &(ル)& 正である &(ヲ)& \frac {4}{3}\pi a^{3}\rho \\[ 5pt ]
&(ワ)& 0 &(カ)& \frac {\sqrt[ 3 ]{ 2 }\rho }{3\varepsilon _{0}}a &(ヨ)& a \ の大きさによって正か負かが変わる \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
一様に電荷を帯びた球の作る電界及び電位に関する問題です。
ガウスの法則を利用する典型的な問題例ですが,やや計算量が多いため朝一の受験生に厳しい問題であったかなと思います。
もし(5)が具体的な式の導出であった場合は\( \ 1 \ \)種レベルの問題と考えて良いでしょう。
1.ガウスの法則
\( \ Q [ \mathrm {C} ] \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本であり,電界\( \ E \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの法則といいます。
2.空間上の電位\( \ V \ \)
中心からの距離\( \ r \ \)に関する電界\( \ E_{\mathrm {r}} \ \)が与えられている時,その場所の電位\( \ V \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)解答:ヲ
半径\( \ r \ \)の球の体積は\( \ \displaystyle \frac {4}{3}\pi r^{3} \ \)であるから,領域\( \ \mathrm {A} \ \)に存在する電荷の合計\( \ Q_{\mathrm {A}} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {A}}&=&\rho \cdot \frac {4}{3}\pi a^{3} \\[ 5pt ]
&=&\frac {4}{3}\pi a^{3}\rho \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
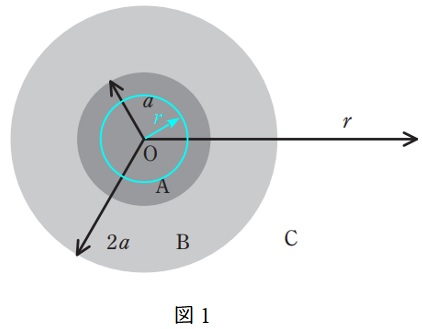
図1に示すように,領域\( \ \mathrm {A} \ \)での半径\( \ r \ \)の球の内側の電荷の合計\( \ Q_{\mathrm {A}}^{\prime } \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {A}}^{\prime }&=&\frac {4}{3}\pi r^{3}\rho \\[ 5pt ]
\end{eqnarray}
\]
であり,半径\( \ r \ \)の球の表面積は\( \ \displaystyle 4\pi r^{2} \ \)であるから,電界\( \ E\left( r\right) \ \)の大きさは,ワンポイント解説「1.ガウスの法則」より,
\[
\begin{eqnarray}
4\pi r^{2}E\left( r\right) &=& \frac {\displaystyle \frac {4}{3}\pi r^{3}\rho }{\varepsilon _{0}} \\[ 5pt ]
E\left( r\right) &=& \frac {\displaystyle \frac {4}{3}\pi r^{3}\rho }{4\pi r^{2}\varepsilon _{0}} \\[ 5pt ]
&=& \frac {\rho }{3\varepsilon _{0}}r \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
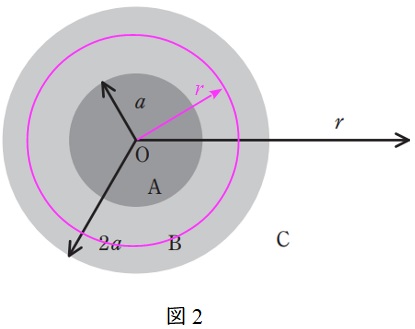
図2に示すように,領域\( \ \mathrm {B} \ \)での半径\( \ r \ \)の球の内側の電荷の合計\( \ Q_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {B}}&=&\rho \cdot \frac {4}{3}\pi a^{3}-\frac {\rho }{7}\left( \frac {4}{3}\pi r^{3}-\frac {4}{3}\pi a^{3}\right) \\[ 5pt ]
&=&\frac {4}{3}\pi a^{3}\rho -\frac {4}{21}\pi r^{3}\rho +\frac {4}{21}\pi a^{3}\rho \\[ 5pt ]
&=&\frac {32}{21}\pi a^{3}\rho -\frac {4}{21}\pi r^{3}\rho \\[ 5pt ]
&=&\frac {4}{21}\pi \left( 8a^{3}- r^{3}\right) \rho \\[ 5pt ]
\end{eqnarray}
\]
であるから,電界\( \ E\left( r\right) \ \)の大きさは,ワンポイント解説「1.ガウスの法則」より,
\[
\begin{eqnarray}
4\pi r^{2}E\left( r\right) &=& \frac {\displaystyle \frac {4}{21}\pi \left( 8a^{3}- r^{3}\right) \rho }{\varepsilon _{0}} \\[ 5pt ]
E\left( r\right) &=& \frac {\displaystyle \frac {4}{21}\pi \left( 8a^{3}- r^{3}\right) \rho }{4\pi r^{2}\varepsilon _{0}} \\[ 5pt ]
&=& \frac {\left( 8a^{3}- r^{3}\right) \rho }{21r^{2}\varepsilon _{0}} \\[ 5pt ]
&=& \frac {\rho }{21\varepsilon _{0}}\left( \frac {8a^{3}}{r^{2}}-r\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ワ
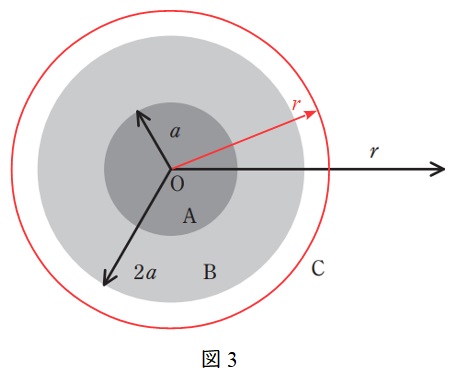
図3に示すように,領域\( \ \mathrm {C} \ \)での半径\( \ r \ \)の球の内側の電荷の合計\( \ Q_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&\rho \cdot \frac {4}{3}\pi a^{3}-\frac {\rho }{7}\left\{ \frac {4}{3}\pi \left( 2a\right) ^{3}-\frac {4}{3}\pi a^{3}\right\} \\[ 5pt ]
&=&\rho \cdot \frac {4}{3}\pi a^{3}-\frac {\rho }{7}\left( \frac {4}{3}\pi\cdot 8a^{3}-\frac {4}{3}\pi a^{3}\right) \\[ 5pt ]
&=&\rho \cdot \frac {4}{3}\pi a^{3}-\frac {\rho }{7}\cdot \frac {4}{3}\pi\left( 8a^{3}-a^{3}\right) \\[ 5pt ]
&=&\rho \cdot \frac {4}{3}\pi a^{3}-\frac {\rho }{7}\cdot \frac {4}{3}\pi \cdot 7a^{3} \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となるので,電界\( \ E\left( r\right) \ \)の大きさは\( \ 0 \ \)と求められる。
(5)解答:ル
領域\( \ \mathrm {A} \ \)のとき\( \ E\left( r\right) >0 \ \),領域\( \ \mathrm {B} \ \)のとき\( \ E\left( r\right) >0 \ \),領域\( \ \mathrm {C} \ \)のとき\( \ E\left( r\right) =0 \ \)なので,中心\( \ \mathrm {O}\left( r=0\right) \ \)の電位\( \ V \ \)は正となる。
【参考】
\( \ r→\infty \ \)の無限遠点を電位の基準とした場合に,中心\( \ \mathrm {O}\left( r=0\right) \ \)の電位\( \ V \ \)は,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{0}E\left( r\right) \mathrm {d}r \\[ 5pt ]
&=&-\int _{\infty }^{2a} 0\mathrm {d}r-\int _{2a}^{a} \frac {\rho }{21\varepsilon _{0}}\left( \frac {8a^{3}}{r^{2}}-r\right) \mathrm {d}r-\int _{a}^{0} \frac {\rho }{3\varepsilon _{0}}r\mathrm {d}r \\[ 5pt ]
&=&-\frac {\rho }{21\varepsilon _{0}}\int _{2a}^{a} \left( \frac {8a^{3}}{r^{2}}-r\right) \mathrm {d}r-\frac {\rho }{3\varepsilon _{0}}\int _{a}^{0} r\mathrm {d}r \\[ 5pt ]
&=&-\frac {\rho }{21\varepsilon _{0}}\left[ -\frac {8a^{3}}{r}-\frac {r^{2}}{2}\right] _{2a}^{a} -\frac {\rho }{3\varepsilon _{0}}\left[ \frac {r^{2}}{2}\right] _{a}^{0} \\[ 5pt ]
&=&-\frac {\rho }{21\varepsilon _{0}}\left\{ \left( -\frac {8a^{3}}{a}-\frac {a^{2}}{2} \right) -\left( -\frac {8a^{3}}{2a}-\frac {4a^{2}}{2} \right) \right\} -\frac {\rho }{3\varepsilon _{0}}\left( 0-\frac {a^{2}}{2}\right) \\[ 5pt ]
&=&-\frac {\rho }{21\varepsilon _{0}}\left( -8a^{2}-\frac {a^{2}}{2} +4a^{2}+2a^{2} \right) +\frac {\rho }{3\varepsilon _{0}}\cdot \frac {a^{2}}{2} \\[ 5pt ]
&=&\frac {\rho }{21\varepsilon _{0}}\cdot \frac {5a^{2}}{2} +\frac {\rho }{3\varepsilon _{0}}\cdot \frac {a^{2}}{2} \\[ 5pt ]
&=&\frac {2\rho }{7\varepsilon _{0}}a^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,中心の電位は正であることがわかる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは