《法規》〈電気施設管理〉[R06:問4]変電所の設備容量の検討に必要な事項に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，変電所の設備容量の検討に必要な事項に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

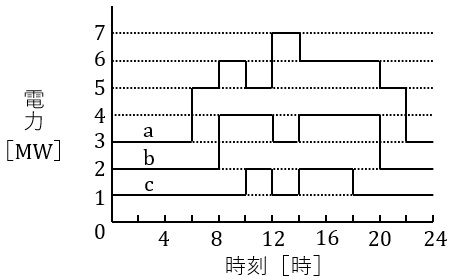
ある変電所において図に示す日負荷曲線を有する三つの負荷\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)及び\( \ \mathrm {c} \ \)に電力を供給している。この変電所の平均需要電力は\( \ \fbox {　 （１） 　} \ \mathrm {MW} \ \)で，総合負荷率は\( \ \fbox {　 （２） 　} \ \mathrm {％} \ \)である。また，不等率は\( \ \fbox {　 （３） 　} \ \)である。

ここで負荷\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)及び\( \ \mathrm {c} \ \)の力率は時間によらず一定で，それぞれ\( \ 60 \ \mathrm {％} \ \)，\( \ 80 \ \mathrm {％} \ \)及び\( \ 100 \ \mathrm {％} \ \)であるとすると，総合負荷が最大となる時刻における総合力率は\( \ \fbox {　 （４） 　} \ \mathrm {％} \ \)であり，この変電所の変圧器に必要な最小容量は\( \ \fbox {　 （５） 　} \ \mathrm {MV\cdot A} \ \)である。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　0.923　　　　　&（ロ）&　1.08　　　　　&（ハ）&　1.18 \\[ 5pt ] &（ニ）&　9.00　　　　　&（ホ）&　17.0　　　　　&（ヘ）&　18.7 \\[ 5pt ] &（ト）&　68.9　　　　　&（チ）&　73.3　　　　　&（リ）&　73.7 \\[ 5pt ] &（ヌ）&　75.0　　　　　&（ル）&　81.8　　　　　&（ヲ）&　133 \\[ 5pt ] &（ワ）&　216　　　　　&（カ）&　9 \ 000　　　　　&（ヨ）&　17 \ 000 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

日負荷曲線から負荷率，不等率，総合力率等を求める問題です。
例年，一次試験では計算問題の出題割合は少なく，本問のような問題は二次試験に出題される傾向にありますが，令和6年は一次試験で出題されることになりました。
少し計算量も多い問題ですが，\( \ 2 \ \)種受験生ですと多くの方が完答してくる問題と予想されます。需要率，不等率，負荷率の定義を確実に覚え，計算間違いに注意し，完答できるようにしましょう。

1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
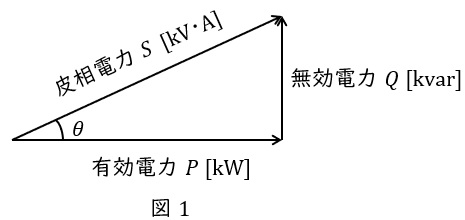
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

2.需要率，不等率，負荷率の定義
①需要率
\[
\begin{eqnarray}
需要率&=&\frac {最大需要電力}{設備容量}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

②不等率（常に\( \ 1 \ \)以上となる)
\[
\begin{eqnarray}
不等率&=&\frac {個々の最大需要電力の合計}{合成の最大需要電力} \\[ 5pt ] \end{eqnarray}
\]

③負荷率
\[
\begin{eqnarray}
負荷率&=&\frac {平均需要電力}{最大需要電力}\times 100　[％] \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ニ
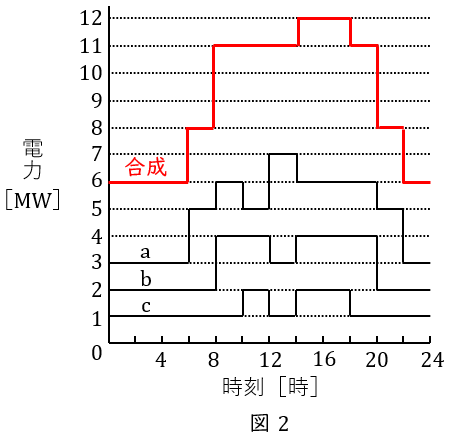
負荷\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)及び\( \ \mathrm {c} \ \)を合わせた合成需要電力は図2の通りとなる。
図2より平均需要電力\( \ P_{\mathrm {av}} \ \mathrm {[MW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {av}}&=&\frac {6\times 6+8\times 2+11\times 6+12\times 4+11\times 2+8\times 2+6\times 2}{24} \\[ 5pt ] &=&9 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヌ
図2より最大需要電力\( \ P_{\mathrm {m}}=12 \ \mathrm {[MW]} \ \)であるから，総合負荷率\( \ \mathrm {[％]} \ \)は，ワンポイント解説「2.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
総合負荷率&=&\frac {P_{\mathrm {av}}}{P_{\mathrm {m}}}\times 100 \\[ 5pt ] &=&\frac {9}{12}\times 100 \\[ 5pt ] &=&75 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ロ
各負荷\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)及び\( \ \mathrm {c} \ \)の最大需要電力\( \ P_{\mathrm {am}}=7 \ \mathrm {[MW]} \ \)，\( \ P_{\mathrm {bm}}=4 \ \mathrm {[MW]} \ \)及び\( \ P_{\mathrm {cm}}=2 \ \mathrm {[MW]} \ \)であるから，不等率は，ワンポイント解説「2.需要率，不等率，負荷率の定義」の通り，
\[
\begin{eqnarray}
不等率&=&\frac {P_{\mathrm {am}}+P_{\mathrm {bm}}+P_{\mathrm {cm}}}{P_{\mathrm {m}}} \\[ 5pt ] &=&\frac {7+4+2}{12} \\[ 5pt ] &≒&1.08 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：リ
図2より総合負荷が最大となる時刻は\( \ 14 \ \)時から\( \ 18 \ \)時の間であることがわかる。このときの負荷\( \ \mathrm {a} \ \)及び\( \ \mathrm {b} \ \)の無効電力\( \ Q_{\mathrm {am}} \ \mathrm {[Mvar]} \ \)及び\( \ Q_{\mathrm {bm}} \ \mathrm {[Mvar]} \ \)は，それぞれの力率\( \ \cos \theta _{\mathrm {a}}=0.6 \ \)及び\( \ \cos \theta _{\mathrm {b}}=0.8 \ \)であるから，ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り，
\[
\begin{eqnarray}
Q_{\mathrm {am}}&=&P_{\mathrm {am}}\tan \theta _{\mathrm {a}} \\[ 5pt ] &=&P_{\mathrm {am}}\frac {\sin \theta _{\mathrm {a}}}{\cos \theta _{\mathrm {a}}} \\[ 5pt ] &=&P_{\mathrm {am}}\frac {\sqrt {1-\cos ^{2}\theta _{\mathrm {a}}}}{\cos \theta _{\mathrm {a}}} \\[ 5pt ] &=&6\times \frac {\sqrt {1-0.6 ^{2}}}{0.6} \\[ 5pt ] &=&6\times \frac {0.8}{0.6} \\[ 5pt ] &=&8 \ \mathrm {[Mvar]} \\[ 5pt ] Q_{\mathrm {bm}}&=&P_{\mathrm {bm}}\tan \theta _{\mathrm {b}} \\[ 5pt ] &=&P_{\mathrm {bm}}\frac {\sin \theta _{\mathrm {b}}}{\cos \theta _{\mathrm {b}}} \\[ 5pt ] &=&P_{\mathrm {bm}}\frac {\sqrt {1-\cos ^{2}\theta _{\mathrm {b}}}}{\cos \theta _{\mathrm {b}}} \\[ 5pt ] &=&4\times \frac {\sqrt {1-0.8 ^{2}}}{0.8} \\[ 5pt ] &=&4\times \frac {0.6}{0.8} \\[ 5pt ] &=&3 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
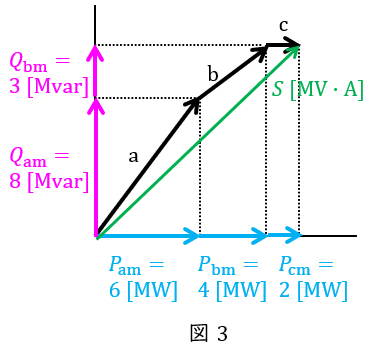
\] となる。これより，負荷\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)及び\( \ \mathrm {c} \ \)をベクトル図で表すと図3のようになる。したがって，全体の総合力率\( \ \cos \theta \ \)は，ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P_{\mathrm {am}}+P_{\mathrm {bm}}+P_{\mathrm {cm}}}{S} \\[ 5pt ] &=&\frac {P_{\mathrm {am}}+P_{\mathrm {bm}}+P_{\mathrm {cm}}}{\sqrt {\left( P_{\mathrm {am}}+P_{\mathrm {bm}}+P_{\mathrm {cm}}\right) ^{2}+\left( Q_{\mathrm {am}}+Q_{\mathrm {bm}}\right) ^{2}}} \\[ 5pt ] &=&\frac {6+4+2}{\sqrt {\left( 6+4+2\right) ^{2}+\left( 8+3\right) ^{2}}} \\[ 5pt ] &≒&\frac {12}{16.279} \\[ 5pt ] &≒&0.737　→　73.7 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
図3より，全体の負荷の皮相電力\( \ S \ \mathrm {[MV\cdot A]} \ \)は，
\[
\begin{eqnarray}
S &=&\sqrt {\left( P_{\mathrm {am}}+P_{\mathrm {bm}}+P_{\mathrm {cm}}\right) ^{2}+\left( Q_{\mathrm {am}}+Q_{\mathrm {bm}}\right) ^{2}} \\[ 5pt ] &=&\sqrt {\left( 6+4+2\right) ^{2}+\left( 8+3\right) ^{2}} \\[ 5pt ] &≒&16.3 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] となるので，必要な最小容量はこれより大きい\( \ 17.0 \ \mathrm {[MV\cdot A]} \ \)と求められる。