《機械》〈同期機〉[H21:問5]円筒形同期発電機の電機子反作用に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，円筒形同期発電機の電機子反作用に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句又は式を解答群の中から選び，その記号をマークシートに記入しなさい。

界磁磁極を同期速度で回転させると，電機子巻線に起電力が発生する。負荷に電力を供給すると電機子電流が流れ，電機子電流の位相によって交差，減磁又は増磁起磁力として作用する。このような作用を電機子反作用という。この様子を遅れ力率で運転されている三相円筒形同期発電機の一相の電機子巻線について，ベクトル（フェーザ）で表すと図のようになる。ただし，誘導起電力を$ \ \dot E \ $，電機子電流を$ \ {\dot I}_{a} \ $，$ \ {\dot I}_{a} \ $による起磁力を$ \ {\dot F}_{a} \ $及び電機子巻線に鎖交する磁束を$ \ \dot {\mathit {\Phi }} \ $とする。電機子電流$ \ {\dot I}_{a} \ $を基準にとると，$ \ {\dot F}_{a} \ $は$ \ {\dot I}_{a} \ $と同相にあって，主界磁起磁力$ \ {\dot F}_{f} \ $との合成起磁力$ \ {\dot F}_{r} \ $による鎖交磁束$ \ \dot {\mathit {\Phi }} \ $によって電機子巻線に誘導される起電力$ \ \dot E \ $は，$ \ {\dot F}_{r} \ $又は$ \ \dot {\mathit {\Phi }} \ $より$ \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ $遅れている。また，無負荷誘導起電力$ \ {\dot E}_{0} \ $は，$ \ {\dot F}_{f} \ $より$ \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ $遅れている。

図において，ベクトル（フェーザ）で$ \ {\dot E}_{0} \ $，$ \ {\dot F}_{f} \ $，$ \ \dot E \ $，$ \ {\dot F}_{r} \ $の大きさには$ \ \displaystyle \frac {E_{0}}{F_{f}}=\frac {E}{F_{r}} \ $の関係があり，また，$ \ ∠\mathrm {aOb} = ∠\mathrm {cOd} \ $であるから$ \ \fbox {　（１）　} \ $は相似である。$ \ \overline {\mathrm {ab}} \ $と$ \ \overline {\mathrm {Oe}} \ $は平行であるから，$ \ \overline {\mathrm {cd}} \ $は$ \ \overline {\mathrm {Oe}} \ $に垂直である。また，$ \ \overline {\mathrm {cd}} \ $は$ \ I_{a} \ $に比例するから，$ \ \overline {\mathrm {cd}}=X_{a}I_{a} \ $とおけば，
\[
\begin{eqnarray}
\dot E&=& \ \fbox {　（２）　} \ \\[ 5pt ] \end{eqnarray}
\] と表すことができるので，電機子反作用による$ \ {\dot E}_{0} \ $から$ \ \dot E \ $への変化を電機子電流による$ \ \fbox {　（３）　} \ $として表したことになる。$ \ E \ $を内部起電力，$ \ X_{a} \ $を電機子$ \ \fbox {　（４）　} \ $という。電機子巻線の抵抗を$ \ R_{a} \ $，漏れリアクタンスを$ \ X_{l} \ $，端子電圧を$ \ \dot V \ $とすれば，電圧関係式は次のようになる。
\[
\begin{eqnarray}
\dot V&=& {\dot E}_{0}-\left( R_{a}+\mathrm {j}X_{s}\right) {\dot I}_{a} \\[ 5pt ] \end{eqnarray}
\] ただし，$ \ X_{s} = \ \fbox {　（５）　} \ $であり，同期リアクタンスという。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　X_{a}+R_{a}　　　　　&（ロ）&　リアクタンス降下　　　　　　　　&（ハ）&　R_{a}+X_{l} \\[ 5pt ] &（ニ）&　△\mathrm {Ocd} \ と \ △\mathrm {Ode}　　　　　&（ホ）&　{\dot E}_{0}-\mathrm {j}X_{a}{\dot I}_{a}　　　　　&（ヘ）&　抵抗降下 \\[ 5pt ] &（ト）&　反作用リアクタンス　　　　　　　　&（チ）&　△\mathrm {Oab} \ と \ △\mathrm {Ode}　　　　　&（リ）&　反作用トルク \\[ 5pt ] &（ヌ）&　{\dot E}_{0}+\mathrm {j}X_{a}{\dot I}_{a}　　　　　&（ル）&　作用リアクタンス　　　　　&（ヲ）&　{\dot E}_{0}-X_{a}{\dot I}_{a} \\[ 5pt ] &（ワ）&　容量性リアクタンス　　　　　&（カ）&　X_{a}+X_{l}　　　　　&（ヨ）&　△\mathrm {Oab} \ と \ △\mathrm {Ocd} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

同期機の電機子反作用に関する問題です。
知識以上に数学的な要素を多く含む問題で選択肢も絞りやすい内容でしたので，文脈から判断し高得点を取得できた受験生も多かったかと思います。
電機子反作用の概念は理解しておいた方が良いかと思います。

1.同期発電機の電機子反作用
同期発電機の電機子反作用は，界磁磁束に電機子巻線による磁束が合成されることにより発生し，その力率により交さ磁化作用，減磁作用，増磁作用が起こります。

①交さ磁化作用
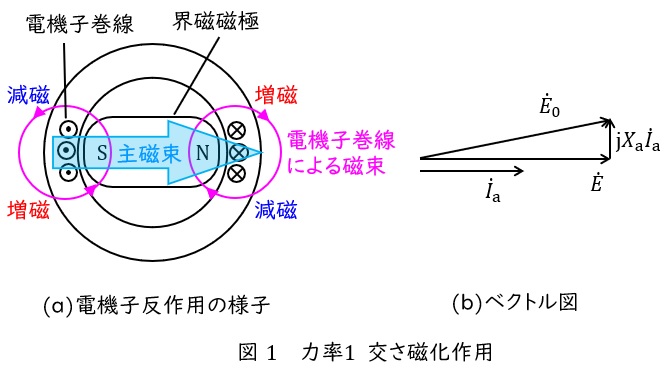
力率$ \ 1 \ $のときは界磁磁極と電機子巻線が図1(a)に示すような関係にあります。
このとき，電機子巻線による磁束は界磁磁極の磁束に対し強め合う部分と弱め合う部分が発生し，これを交さ磁化作用といいます。
このときの無負荷誘導起電力を$ \ {\dot E}_{0} \ $，誘導起電力を$ \ \dot E \ $，電機子電流を$ \ {\dot I}_{\mathrm {a}} \ $，電機子反作用リアクタンスを$ \ X_{\mathrm {a}} \ $とすると，ベクトル図は図1(b)のようになります。増磁作用は磁気飽和のため増加割合が低く，全体としては減磁し無負荷誘導起電力$ \ {\dot E}_{0} \ $よりも誘導起電力$ \ \dot E \ $の方が小さくなります。

②減磁作用
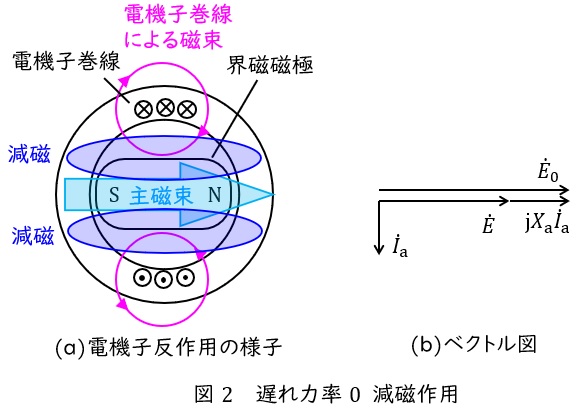
遅れ力率$ \ 0 \ $のときは界磁磁極と電機子巻線が図2(a)に示すような関係にあります。
このとき，電機子巻線による磁束は界磁磁極の磁束を弱め，これを減磁作用といいます。
このときの無負荷誘導起電力を$ \ {\dot E}_{0} \ $，誘導起電力を$ \ \dot E \ $，電機子電流を$ \ {\dot I}_{\mathrm {a}} \ $，電機子反作用リアクタンスを$ \ X_{\mathrm {a}} \ $とすると，ベクトル図は図2(b)のようになります。ベクトル図からも$ \ {\dot E}_{0} ＞ \dot E \ $となることがわかるかと思います。

③増磁作用
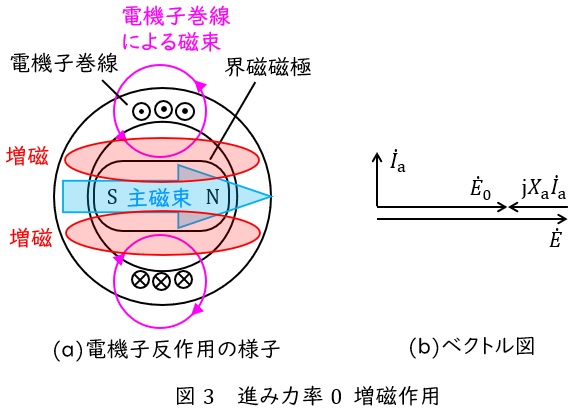
進み力率$ \ 0 \ $のときは界磁磁極と電機子巻線が図3(a)に示すような関係にあります。
このとき，電機子巻線による磁束は界磁磁極の磁束を強め，これを増磁作用といいます。
このときの無負荷誘導起電力を$ \ {\dot E}_{0} \ $，誘導起電力を$ \ \dot E \ $，電機子電流を$ \ {\dot I}_{\mathrm {a}} \ $，電機子反作用リアクタンスを$ \ X_{\mathrm {a}} \ $とすると，ベクトル図は図3(b)のようになります。ベクトル図からも$ \ {\dot E}_{0} ＜ \dot E \ $となることがわかるかと思います。

【解答】

(1)解答：ヨ
題意より解答候補は，（ニ）$ \ △\mathrm {Ocd} \ $と$ \ △\mathrm {Ode} \ $，（チ）$ \ △\mathrm {Oab} \ $と$ \ △\mathrm {Ode} \ $，（ヨ）$ \ △\mathrm {Oab} \ $と$ \ △\mathrm {Ocd} \ $，になると思います。
$ \ \displaystyle \frac {E_{0}}{F_{f}}=\frac {E}{F_{r}} \ $及び$ \ ∠\mathrm {aOb} = ∠\mathrm {cOd} \ $より，$ \ △\mathrm {Oab} \ $と$ \ △\mathrm {Ocd} \ $は$ \ 2 \ $組の辺の比とその間の角の大きさが等しいので，相似条件を満たすことになります。

(2)解答：ホ
題意より解答候補は，（ホ）$ \ {\dot E}_{0}-\mathrm {j}X_{a}{\dot I}_{a} \ $，（ヌ）$ \ {\dot E}_{0}+\mathrm {j}X_{a}{\dot I}_{a} \ $，（ヲ）$ \ {\dot E}_{0}-X_{a}{\dot I}_{a} \ $，になると思います。
問題図において$ \ \mathrm {j}X_{a}{\dot I}_{a} \ $は点$ \ \mathrm {d} \ $から点$ \ \mathrm {c} \ $へ向かうベクトルなので，$ \ \dot E={\dot E}_{0}-\mathrm {j}X_{a}{\dot I}_{a} \ $の関係があります。

(3)解答：ロ
題意より解答候補は，（ロ）リアクタンス降下，（ヘ）抵抗降下，（リ）反作用トルク，になると思います。
$ \ \mathrm {j}X_{a}{\dot I}_{a} \ $はリアクタンスによる電圧降下なのでリアクタンス降下が正しいです。

(4)解答：ト
題意より解答候補は，（ト）反作用リアクタンス，（ル）作用リアクタンス，（ワ）容量性リアクタンス，になると思います。
ワンポイント解説「1.同期発電機の電機子反作用」でも使用していますが，電機子反作用によるリアクタンスを電機子反作用リアクタンスといいます。

(5)解答：カ
題意より解答候補は，（イ）$ \ X_{a}+R_{a} \ $，（ハ）$ \ R_{a}+X_{l} \ $，（カ）$ \ X_{a}+X_{l} \ $，になると思います。
同期リアクタンスは電機子反作用リアクタンスと漏れリアクタンスを合わせたもので$ \ X_{s}=X_{a}+X_{l} \ $の関係があります。$ \ \dot V= {\dot E}_{0}-\left( R_{a}+\mathrm {j}X_{s}\right) {\dot I}_{a} \ $の式に既に$ \ R_{a} \ $が含まれているため$ \ R_{a} \ $を含む選択肢は除外しても良いかと思います。