Contents
【問題】
【難易度】★★★☆☆(普通)
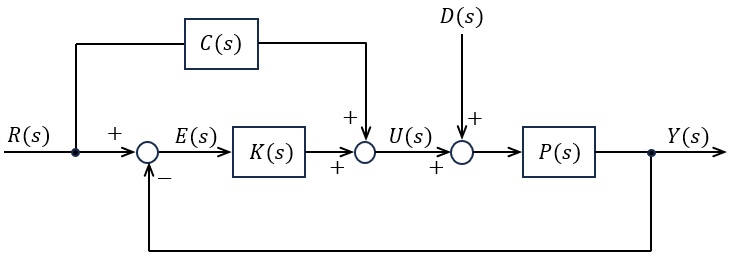
次の文章は,図に示す二つの補償器を含む\( \ 2 \ \)自由度制御系に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句,式又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。ただし,\( \ R\left( s\right) \ \)は目標値,\( \ E\left( s\right) \ \)は偏差,\( \ D\left( s\right) \ \)は外乱,\( \ U\left( s\right) \ \)は操作量,\( \ Y\left( s\right) \ \)は出力を表す。また,\( \ P\left( s\right) \ \)は制御対象,\( \ K\left( s\right) \ \)と\( \ C\left( s\right) \ \)はそれぞれの補償器の伝達関数とする。
図の制御系において,\( \ R\left( s\right) =0 \ \)のとき,\( \ D\left( s\right) \ \)から\( \ E\left( s\right) \ \)までの伝達関数は\( \ \fbox { (1) } \ \)で与えられ,補償器\( \ C\left( s\right) \ \)によらない。補償器\( \ C\left( s\right) \ \)は,\( \ \fbox { (2) } \ \)と呼ばれ,\( \ \fbox { (3) } \ \)特性を改善する目的で導入される補償器である。図から,\( \ D\left( s\right) =0 \ \)のとき,\( \ R\left( s\right) \ \)から\( \ E\left( s\right) \ \)までの伝達関数は\( \ \fbox { (4) } \ \)となる。
いま,\( \ \displaystyle P\left( s\right) =\frac {1}{s+1} \ \),\( \ \displaystyle K\left( s\right) =K_{c} \ \),\( \ D\left( s\right) =0 \ \)のとき,\( \ C\left( s\right) =0 \ \)の場合は,単位ステップ関数の目標値\( \ R\left( s\right) \ \)に対する定常位置偏差は,\( \ \displaystyle \frac {1}{1+K_{c}} \ \)となるが,一方,\( \ \displaystyle C\left( s\right) =C_{c} \ \)を導入した場合は,\( \ C_{c}= \ \fbox { (5) } \ \)と選ぶことによって定常位置偏差を零にできる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& フィードバック補償器 &(ロ)& -\frac {K\left( s\right) }{1+K\left( s\right) P\left( s\right) } &(ハ)& 1 \\[ 5pt ]
&(ニ)& -\frac {K\left( s\right) P\left( s\right) }{1+K\left( s\right) P\left( s\right) } &(ホ)& 減 衰 &(ヘ)& -\frac {1+C\left( s\right) P\left( s\right) }{1+K\left( s\right) P\left( s\right) } \\[ 5pt ]
&(ト)& フィードフォワード補償器 &(チ)& -1 &(リ)& 目標値追従 \\[ 5pt ]
&(ヌ)& 外乱抑制 &(ル)& \frac {1-C\left( s\right) P\left( s\right) }{1+K\left( s\right) P\left( s\right) } &(ヲ)& 安定化補償器 \\[ 5pt ]
&(ワ)& \frac {1+C\left( s\right) P\left( s\right) }{1+K\left( s\right) P\left( s\right) } &(カ)& 2 &(ヨ)& -\frac {P\left( s\right) }{1+K\left( s\right) P\left( s\right) } \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ 2 \ \)自由度制御系の伝達関数の考え方に関する問題です。
少し(4)と(5)の計算が多いですが,丁寧に計算するようにしましょう。また,求める伝達関数が\( \ R\left( s\right) \ \)から\( \ E\left( s\right) \ \)までであることにも注意して下さい。
\( \ 2 \ \)種では二次試験の問4で自動制御が出題されるため,一次試験での出題は\( \ 3 \ \)種と比較してもかなり少ないです。
この辺りも念頭において分野毎の勉強のバランスを調整するようにして下さい。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
2.ブロック線図の考え方
①直列
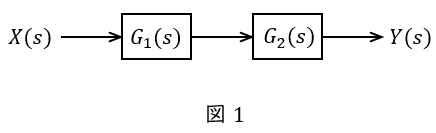
図1のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
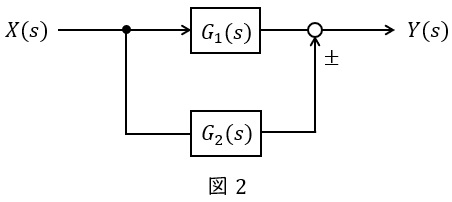
図2のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
③フィードバック
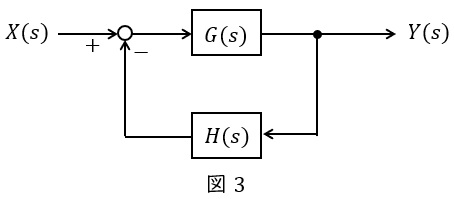
図3のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.ブロック線図の等価変換
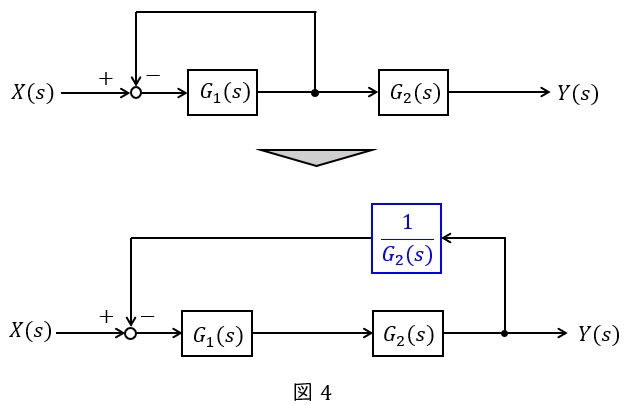
\( \ 2 \ \)自由度制御系等やや複雑なブロック線図には点の移動により等価変換を行います。
例えば図4のようなブロック線図があるとき,\( \ G_{2}\left( s \right) \ \)の手前にある点を後ろに持っていく場合,伝達関数\( \ \displaystyle \frac {1}{G_{2}\left( s \right) } \ \)を入れることで等価変換をすることができます。
4.自動制御の分類
①フィードバック制御
制御量と目標値を比較して,それらを一致させるように操作量を決定する制御です。
例えば汽力発電所の蒸気温度制御や蒸気圧力制御,給水の流量制御等があります。
②フィードフォワード制御
目標値,外乱等の情報から,操作量を決定する制御です。
フィードバック制御では外乱が発生してから対応するため,制御動作が遅くなりやすい性質がありますが,フィードフォワード制御により外乱が発生する前に予測し操作量を決定することが可能となります。
通常フィードバック制御に補償回路を挿入したようなロジック回路が組まれます。
③シーケンス制御
あらかじめ定められた論理回路の順序に従い,各段階を逐次進めていく制御で,以下の二つの種類があります。例えばエレベータ等はシーケンス制御となります。
a.リレーシーケンス
接点を有する電磁継電器を用いたシーケンスで有接点シーケンスともいいます。
b.ロジックシーケンス
半導体論理素子をスイッチとして利用したシーケンスで無接点シーケンスともいいます。
5.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
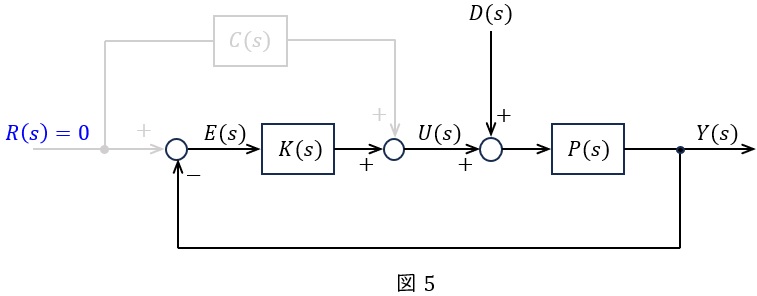
(1)解答:ヨ
\( \ R\left( s\right) =0 \ \)の時のブロック線図は図5のようになる。
図5より,
\[
\begin{eqnarray}
E\left( s \right) &=&\left\{ E\left( s \right) \cdot K\left( s \right) +D\left( s \right) \right\} \cdot P\left( s \right) \cdot \left( -1\right) \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,これを整理すると,
\[
\begin{eqnarray}
E\left( s \right) &=&-E\left( s \right) K\left( s \right) P\left( s \right) -D\left( s \right) P\left( s \right) \\[ 5pt ]
E\left( s \right) +E\left( s \right) K\left( s \right) P\left( s \right) &=&-D\left( s \right) P\left( s \right) \\[ 5pt ]
\left\{ 1+K\left( s \right) P\left( s \right) \right\} E\left( s \right) &=&-D\left( s \right) P\left( s \right) \\[ 5pt ]
\frac {E\left( s \right) }{D\left( s \right) }&=&-\frac {P\left( s\right) }{1+K\left( s\right) P\left( s\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ト
題意より解答候補は,(イ)フィードバック補償器,(ト)フィードフォワード補償器,(ヲ)安定化補償器,になると思います。
ワンポイント解説「4.自動制御の分類」の通り,補償器\( \ C \left( s \right) \ \)は出力\( \ Y \left( s \right) \ \)ではなく予め目標値\( \ R \left( s \right) \ \)の信号を入れているため,フィードフォワード補償器となります。
(3)解答:リ
題意より解答候補は,(ホ)減衰,(リ)目標値追従,(ヌ)外乱抑制,になると思います。
補償器\( \ C \left( s \right) \ \)により,減衰特性や外乱抑制の効果は全くないとまでは言えませんが,最も改善され,目的として適切なのは目標値追従特性となります。
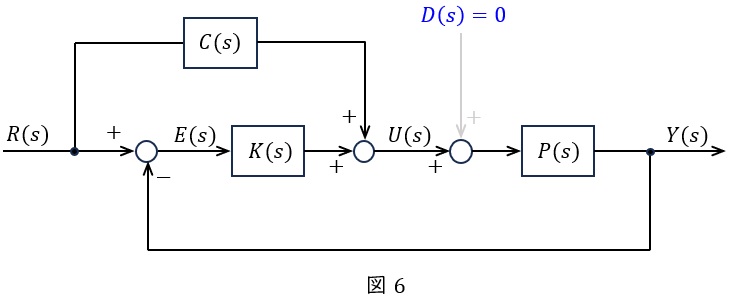
(4)解答:ル
\( \ D\left( s\right) =0 \ \)としたブロック線図は図6のようになる。
図6より,
\[
\begin{eqnarray}
E\left( s \right) &=&\left\{ E\left( s \right) K\left( s \right) +R\left( s \right) C\left( s \right) \right\} P\left( s \right) \cdot \left( -1\right) +R\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
の関係があるから,これを整理すると,
\[
\begin{eqnarray}
E\left( s \right) &=&-K\left( s \right)P\left( s \right)E\left( s \right) -C\left( s \right) P\left( s \right) R\left( s \right) +R\left( s \right) \\[ 5pt ]
E\left( s \right) +K\left( s \right)P\left( s \right)E\left( s \right) &=&R\left( s \right)-C\left( s \right) P\left( s \right) R\left( s \right) \\[ 5pt ]
\left\{ 1+K\left( s \right)P\left( s \right) \right\} E\left( s \right) &=&\left\{ 1-C\left( s \right) P\left( s \right) \right\} R\left( s \right) \\[ 5pt ]
\frac {E\left( s \right) }{R\left( s \right) }&=&\frac {1-C\left( s\right) P\left( s\right) }{1+K\left( s\right) P\left( s\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ハ
\( \ \displaystyle P\left( s\right) =\frac {1}{s+1} \ \),\( \ \displaystyle K\left( s\right) =K_{c} \ \),\( \ D\left( s\right) =0 \ \),\( \ C\left( s\right) =C_{c} \ \)のとき,(4)解答式は,
\[
\begin{eqnarray}
\frac {E\left( s \right) }{R\left( s \right) }&=&\frac {\displaystyle 1-C_{c}\cdot \frac {1}{s+1} }{\displaystyle 1+K_{c}\cdot \frac {1}{s+1} } \\[ 5pt ]
&=&\frac {\displaystyle 1-\frac {C_{c}}{s+1} }{\displaystyle 1+\frac {K_{c}}{s+1} } \\[ 5pt ]
&=&\frac {\displaystyle s+1-C_{c}}{\displaystyle s+1+K_{c} } \\[ 5pt ]
E\left( s \right) &=&\frac {\displaystyle s+1-C_{c}}{\displaystyle s+1+K_{c} }R\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
と変形できる。ワンポイント解説「1.基本的なラプラス変換」の通り,単位ステップ関数\( \ r\left( t\right) =u\left( t\right) \ \)のラプラス変換は\( \ \displaystyle R\left( s\right) =\frac {1}{s} \ \)なので,
\[
\begin{eqnarray}
E\left( s \right) &=&\frac {\displaystyle s+1-C_{c}}{\displaystyle s+1+K_{c} }\frac {1}{s} \\[ 5pt ]
\end{eqnarray}
\]
となり,定常位置偏差は,ワンポイント解説「5.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ s \to 0 } sE(s)&=&\displaystyle \lim _{ s \to 0 } \left\{ s\cdot \frac {\displaystyle s+1-C_{c}}{\displaystyle s+1+K_{c} }\frac {1}{s} \right\} \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left\{ \frac {\displaystyle s+1-C_{c}}{\displaystyle s+1+K_{c} } \right\} \\[ 5pt ]
&=&\frac {\displaystyle 0+1-C_{c}}{\displaystyle 0+1+K_{c} } \\[ 5pt ]
&=&\frac {\displaystyle 1-C_{c}}{\displaystyle 1+K_{c} } \\[ 5pt ]
\end{eqnarray}
\]
となるので,定常位置偏差が零となるためには,\( \ C_{c}=1 \ \)とする必要がある。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは