Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,単相変圧器の三相結線に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
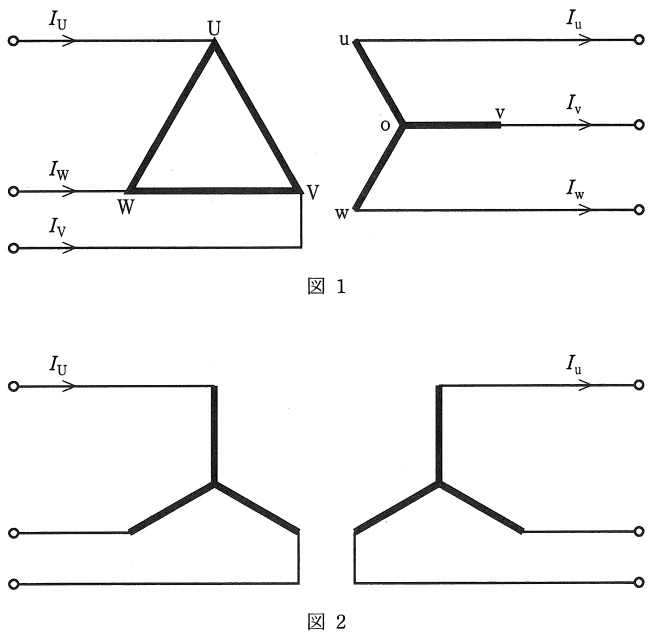
図1は変圧器の\( \ \Delta \ – \mathrm {Y} \ \)結線の説明図である。\( \ \mathrm {U} \ – \mathrm {V} \ \)と\( \ \mathrm {u} \ – \mathrm {o} \ \)からなる単相変圧器について考える。この変圧器の一次電圧\( \ V_{\mathrm {UV}} \ \)と二次電圧\( \ V_{\mathrm {uo}} \ \)とは同相であるが,無負荷のときの二次の線間電圧\( \ V_{\mathrm {uv}} \ \)は大きさが\( \ V_{\mathrm {uo}} \ \)の\( \ \sqrt {3} \ \)倍となり,位相は一次線間電圧\( \ V_{\mathrm {UV}} \ \)より\( \ \fbox { (1) } \ \)いる。この位相差を無視して,電圧及び電流の大きさを求めるための簡易等価回路は,一次側の\( \ \Delta \ \)結線を等価な\( \ \mathrm {Y} \ \)結線に変換し,次の手順で導かれる。
図1における各単相変圧器の一次と二次との巻数の比を\( \ a:1 \ \),その一次漏れインピーダンスを\( \ Z_{1} \ \)とする。図2を図1の\( \ \Delta \ – \mathrm {Y} \ \)結線と等価な\( \ \mathrm {Y} \ – \mathrm {Y} \ \)結線とすると,一次漏れインピーダンスは\( \ \fbox { (2) } \ \)となる。励磁電流を無視し,一次と二次との巻数の比を\( \ a^{\prime }:1 \ \)とすると,図1と図2の線電流\( \ I_{\mathrm {U}} \ \),\( \ I_{\mathrm {u}} \ \)それぞれの大きさを不変とするには,\( \ I_{\mathrm {u}}=a^{\prime }I_{\mathrm {U}}= \ \fbox { (3) } \ I_{\mathrm {U}} \ \)が必要である。したがって,二次の漏れインピーダンス\( \ Z_{\mathrm {2}} \ \)を一次に換算すると,\( \ \fbox { (4) } \ \)となる。励磁電流を考慮するには図1の各変圧器の励磁アドミタンス\( \ Y_{\mathrm {0}} \ \)を\( \ \fbox { (5) } \ \)倍して星形に接続したものを付加すればよい。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 3Z_{\mathrm {1}} &(ロ)& \frac {Z_{\mathrm {1}}}{3} &(ハ)& \sqrt {3}a \\[ 5pt ]
&(ニ)& 3a^{2}Z_{\mathrm {2}} &(ホ)& 3 &(ヘ)& \frac {Z_{\mathrm {1}}}{\sqrt {3}} \\[ 5pt ]
&(ト)& 30 \ \left[ ° \right] \ 遅れて &(チ)& 60 \ \left[ ° \right] \ 進んで &(リ)& \frac {a}{\sqrt {3}} \\[ 5pt ]
&(ヌ)& 30 \ \left[ ° \right] \ 進んで &(ル)& \frac {1}{3} &(ヲ)& \frac {1}{a} \\[ 5pt ]
&(ワ)& \sqrt {3} &(カ)& \frac {a^{2}Z_{\mathrm {2}}}{3} &(ヨ)& \frac {Z_{\mathrm {2}}}{a^{2}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ \Delta \ – \mathrm {Y} \ \)結線をした変圧器の電圧や電流,インピーダンスの一次二次換算に関する問題です。
理論科目で習得する\( \ \Delta \ – \mathrm {Y} \ \)変換や相電圧と線間電圧の関係等を利用した問題となっているため,\( \ 2 \ \)種らしい科目を超えた総合的な問題となっています。
しっかりとした知識を身につけていれば得点できる良問であると思います。
1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
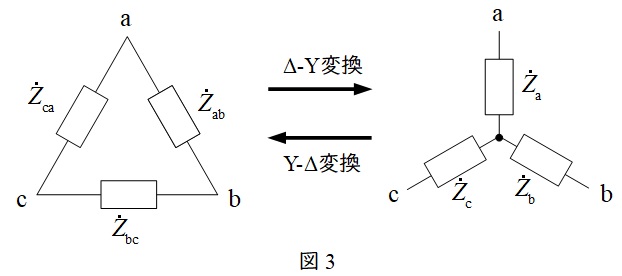
図3において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図3において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\]
となります。
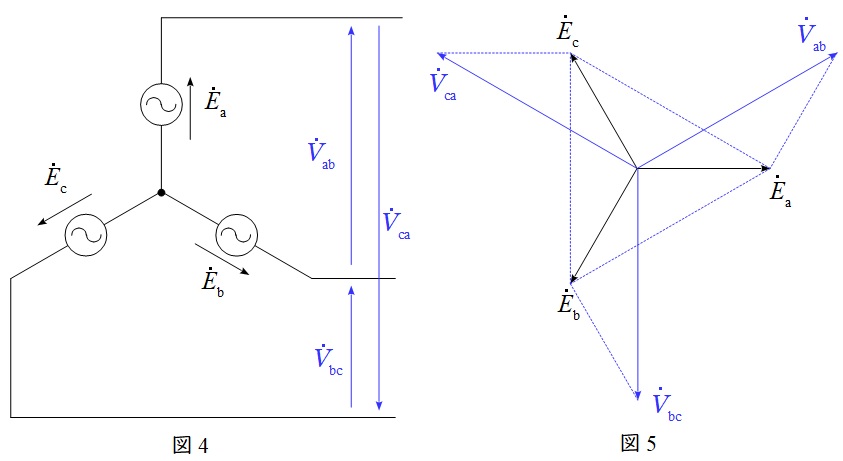
2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
図4のような三相対称電源がある時,線間電圧と相電圧の関係は図5のベクトル図のようになり,線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると,
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ]
V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ]
V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)進みであることが分かります。
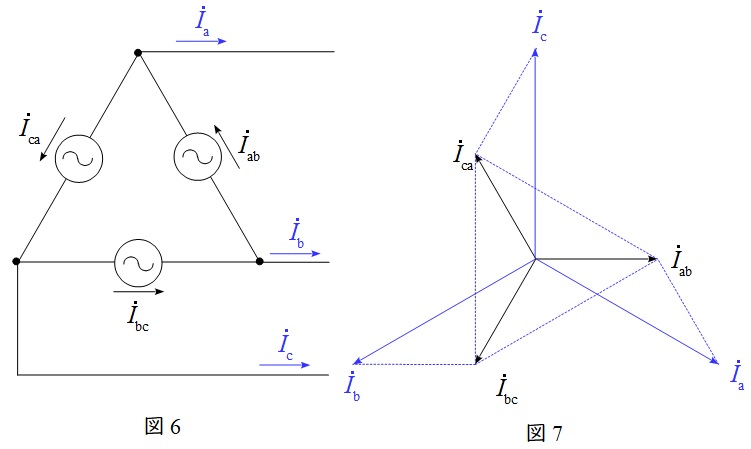
3.\( \ \Delta \ \)結線における相電流と線電流の関係
図6のような三相対称電源がある時,線電流と相電流の関係は図7のベクトル図のようになり,線電流の大きさは相電流の大きさと比較すると,
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ]
I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ]
I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)遅れであることが分かります。
【解答】
(1)解答:ヌ
ワンポイント解説「2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り,二次の線間電圧\( \ V_{\mathrm {uv}} \ \)は二次の相電圧\( \ V_{\mathrm {uo}} \ \)より\( \ 30 \ \left[ ° \right] \ \)進んでいるため,一次の線間電圧\( \ V_{\mathrm {UV}} \ \)よりも\( \ 30 \ \left[ ° \right] \ \)進んでいることがわかる。
(2)解答:ロ
ワンポイント解説「1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り,平衡三相回路においては,\( \ \mathrm {Y} \ \)結線のインピーダンスは\( \ \Delta \ \)結線の\( \ \displaystyle \frac {1}{3} \ \)倍にすれば等価変換可能となるので,一次漏れインピーダンスは\( \ \displaystyle \frac {Z_{\mathrm {1}}}{3} \ \)と求められる。
(3)解答:リ
ワンポイント解説「3.\( \ \Delta \ \)結線における相電流と線電流の関係」の通り,\( \ \Delta \ \)結線においては,相電流は線電流の\( \ \displaystyle \frac {1}{\sqrt {3}} \ \)倍であり,二次電流は一次電流の\( \ a \ \)倍となるから,
\[
\begin{eqnarray}
I_{\mathrm {u}} &=&a\cdot \frac {1}{\sqrt {3}}I_{\mathrm {U}} \\[ 5pt ]
&=&\frac {a}{\sqrt {3}}I_{\mathrm {U}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:カ
二次の線間電圧\( \ V_{\mathrm {uv}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {uv}} &=&\sqrt {3}V_{\mathrm {uo}} \\[ 5pt ]
&=&\frac {\sqrt {3}}{a}V_{\mathrm {UV}} \\[ 5pt ]
\end{eqnarray}
\]
であるため,インピーダンス\( \ \displaystyle Z=\frac {V_{\mathrm {UV}}}{I_{\mathrm {U}}} \ \)を二次換算すると,
\[
\begin{eqnarray}
Z^{\prime } &=&\frac {\displaystyle \frac {\sqrt {3}}{a}V_{\mathrm {UV}}}{\displaystyle \frac {a}{\sqrt {3}}I_{\mathrm {U}}} \\[ 5pt ]
&=&\frac {3}{a^{2}}Z \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,二次の漏れインピーダンス\( \ Z_{\mathrm {2}} \ \)を一次に換算すると,\( \ \displaystyle \frac {a^{2}Z_{\mathrm {2}}}{3} \ \)と求められる。
(5)解答:ホ
ワンポイント解説「1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り,\( \ \Delta \ – \mathrm {Y} \ \)変換はインピーダンスは\( \ \displaystyle \frac {1}{3} \ \)倍なので,アドミタンスはその逆数となり,\( \ 3 \ \)倍すればよい。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは